Acyclic group
2020 Mathematics Subject Classification: Primary: 20J05 [MSN][ZBL]
A group having the same constant coefficient homology as the trivial group (cf. also Homology). This means that its classifying space is an acyclic space. In the literature the earliest examples are Higman's four-generator four-relator group [Hi]
$$\langle x_0, x_1, x_2, x_3 : x_{i+1}x_ix_{i+1}^{-1} = x_i^2, i\in \mathbb{Z}/4\rangle$$
and others found in combinatorial group theory [BaGr], [BaDyHe], [BeMi]. Further examples arise in geometry ([Ep], [Ma], [Se], [SaVa], [GrSe]) or as automorphism groups of large objects ([HaMc]; for example, the group of all bijections of an infinite set). Algebraically closed groups are acyclic.
Many proofs of acyclicity of infinitely generated groups rely on the property that all binate groups are acyclic [Be3] (cf. also Binate group). An important result in the plus-construction approach to the higher algebraic $K$-theory of rings and operator algebras is that the infinite general linear group of the cone of a ring is acyclic [Wa], [Be]. Topologically, the plus-construction of a topological space is completely determined by a certain perfect, locally free, and hence acyclic, group [BeCa].
Ubiquity results for acyclic groups include the following:
Every perfect group is the homomorphic image of an acyclic group [He].
Every group is a normal subgroup of a normal subgroup of an acyclic group. This result has applications to algebraic topology [KaTh].
Every Abelian group is the centre of an acyclic group [BaDyHe], [Be2].
In contrast to the above are results indicating that acyclic groups have "few" normal subgroups. Thus, the following acyclic groups admit no non-trivial finite-dimensional linear representations over any field:
algebraically closed groups;
Higman's group [Hi];
torsion-generated acyclic groups [Be4];
binate groups [AlBe];
the automorphisms groups of [HaMc], see [Be5], [Be6].
Moreover, many of the above groups are simple modulo the centre.
References
| [AlBe] | R.C. Alperin, A.J. Berrick, "Linear representations of binate groups" J. Pure Appl. Algebra, 94 (1994) pp. 17–23 MR1277521 Zbl 0813.20060 |
| [BaDyHe] | G. Baumslag, E. Dyer, A. Heller, "The topology of discrete groups" J. Pure Appl. Algebra, 16 (1980) pp. 1–47 MR0549702 Zbl 0419.20026 |
| [BaGr] | G. Baumslag, K.W. Gruenberg, "Some reflections on cohomological dimension and freeness" J. Algebra, 6 (1967) pp. 394–409 MR0232827 |
| [Be] | A.J. Berrick, "An approach to algebraic 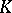 -theory", Pitman (1982) MR649409 -theory", Pitman (1982) MR649409
|
| [Be2] | A.J. Berrick, "Two functors from abelian groups to perfect groups" J. Pure Appl. Algebra, 44 (1987) pp. 35–43 MR0885094 |
| [Be3] | A.J. Berrick, "Universal groups, binate groups and acyclicity", Proc. 1987 Singapore Group Theory Conf., W. de Gruyter (1989) MR0981847 Zbl 0663.20053 |
| [Be4] | A.J. Berrick, "Remarks on the structure of acyclic groups" Bull. London Math. Soc., 22 (1990) pp. 227–232 MR1041135 Zbl 0749.20001 |
| [Be5] | A.J. Berrick, "Groups with no nontrivial linear representations" Bull. Austral. Math. Soc., 50 (1994) pp. 1–11 MR1285653 Zbl 0815.20026 |
| [Be6] | A.J. Berrick, "Corrigenda: Groups with no nontrivial linear representations" Bull. Austral. Math. Soc., 52 (1995) pp. 345–346 MR1348495 |
| [BeCa] | A.J. Berrick, C. Casacuberta, "A universal space for plus-constructions" Topology (to appear) MR1670384 Zbl 0933.55016 |
| [BeMi] | A.J. Berrick, C.F. Miller, III, "Strongly torsion generated groups" Proc. Cambridge Philos. Soc., 111 (1992) pp. 219–229 MR1142741 Zbl 0762.20017 |
| [Ep] | D.B.A. Epstein, "A group with zero homology" Proc. Cambridge Philos. Soc., 68 (1968) pp. 599–601 MR0229692 Zbl 0162.27502 Zbl 0157.30703 |
| [GrSe] | P. Greenberg, V. Sergiescu, "An acyclic extension of the braid group" Comment. Math. Helv., 66 (1991) pp. 109–138 MR1090167 Zbl 0736.20020 |
| [HaMc] | P. de la Harpe, D. McDuff, "Acyclic groups of automorphisms" Comment. Math. Helv., 58 (1983) pp. 48–71 Zbl 0522.20034 |
| [He] | A. Heller, "On the homotopy theory of topogenic groups and groupoids" Ill. Math. J., 24 (1980) pp. 576–605 MR0586797 Zbl 0458.18006 |
| [Hi] | G. Higman, "A finitely generated infinite simple group" J. London Math. Soc., 26 (1951) pp. 61–64 MR0038348 Zbl 0042.02201 |
| [KaTh] | D.M. Kan, W.P. Thurston, "Every connected space has the homology of a 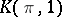 " Topology, 15 (1976) pp. 253–258 MR0413089 Zbl 0355.55004 " Topology, 15 (1976) pp. 253–258 MR0413089 Zbl 0355.55004
|
| [Ma] | J.N. Mather, "The vanishing of the homology of certain groups of homeomorphisms" Topology, 10 (1971) pp. 297–298 MR0288777 Zbl 0207.21903 |
| [SaVa] | P. Sankaran, K. Varadarajan, "Acyclicity of certain homeomorphism groups" Canad. J. Math., 42 (1990) pp. 80–94 MR1043512 Zbl 0711.57022 |
| [Se] | G.B. Segal, "Classifying spaces related to foliations" Topology, 17 (1978) pp. 367–382 MR0516216 Zbl 0398.57018 |
| [Wa] | J.B. Wagoner, "Developping classifying spaces in algebraic 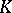 -theory" Topology, 11 (1972) pp. 349–370 -theory" Topology, 11 (1972) pp. 349–370
|
Acyclic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Acyclic_group&oldid=35367