Action
A functional expressed by the definite integral of a function, the stationary values of which determine a real motion of a mechanical system acted upon by given active forces, in the class of kinematically possible motions between some two final positions 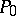 and
and 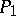 in space and satisfying certain conditions.
in space and satisfying certain conditions.
One distinguishes between Hamiltonian, Lagrangian and Jacobian actions, which appear in the corresponding principles of stationary action.
The Hamiltonian action
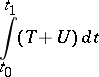 |
is defined in the class of kinematically possible motions of a holonomic system for which the initial and the final positions of the system, as well as the time of motion between them, are the same as the respective ones for real motion.
The Lagrangian action
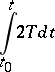 |
and the Jacobian action
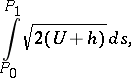 |
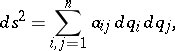 |
are defined in the class of kinematically possible motions of a holonomic conservative system for which the initial and the final positions of the system, and the constant energy 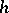 , are the same as the respective magnitudes for a real motion. Here
, are the same as the respective magnitudes for a real motion. Here  is the kinetic energy of the system, and for a conservative system
is the kinetic energy of the system, and for a conservative system
 |
where 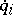 are the generalized Lagrange coordinates, and
are the generalized Lagrange coordinates, and 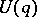 is the force function of active forces.
is the force function of active forces.
For more details see Variational principles of classical mechanics; Hamilton–Ostrogradski principle; Lagrange principle; Jacobi principle.
Action. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Action&oldid=13315