Abstract algebraic logic
The study of logical equivalence, more precisely, the study of the relationship between logical equivalence and logical truth. Meta-logical investigations take on a different character when the emphasis is placed on logical equivalence, one that is very algebraic in character. But, in contrast to traditional algebraic logic, abstract algebraic logic focuses on the process by which a class of algebras is associated with a logical system rather than the algebras that are obtained in the process. The strength of the connection between logical equivalence and logical truth can vary greatly depending on the particular logical system under consideration. One of the main tasks of abstract algebraic logic is the classification of logical systems based on the strength of this connection. It is very strong in classical logic and this gives classical logic its distinctly algebraic character.
The way in which the algebras arise from logic has traditionally followed two distinct paths. The first is based on semantical considerations. In this approach the algebras are abstracted directly from a primitive intuitive notion of logical equivalence, and the assertional aspect of the logic (the notion of logical truth) is expressed in its terms. The development of classical propositional logic (cf. also Propositional calculus) followed this path with Boolean algebras coming before the classical propositional calculus (cf. also Boolean algebra). Relation algebras and the way they arose from the calculus of relations is the modern paradigm for the semantics-based method. In the logistic approach, or rule-based approach, the process is inverted. The assertional part comes first and logical equivalence and the associated algebras are then defined by means of the so-called Lindenbaum–Tarski process. The paradigm for the logistic method is the intuitionistic propositional calculus, where the class of Heyting algebras is constructed from Heyting's formalization of Brouwer's intuitionism by the Lindenbaum–Tarski process (cf. also Heyting formal system). Cylindric and polyadic algebras were obtained by applying the semantics-based method to first-order predicate logic, but, at least in the case of cylindric algebras, the influence of the logistic approach is strongly evident.
The basis of the abstract form of logical equivalence is Frege's principle that sentences, like proper names, have a denotation and that this denotation is their truth value. Two sentences are logically equivalent if they have the same denotation in every possible situation. Thus, according to Frege's principle, they are logically equivalent if they are true in exactly the same interpretations of the underlying uninterpreted logic. For logistic systems this principle has the following technical ramifications.
By a language type one means a set 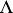 of connectives or operation symbols (cf. also Propositional connective), depending on whether one views them from a logical or algebraic perspective. Each connective has associated with it a natural number, called its rank or arity. The set
of connectives or operation symbols (cf. also Propositional connective), depending on whether one views them from a logical or algebraic perspective. Each connective has associated with it a natural number, called its rank or arity. The set 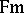 of formulas (terms in an algebraic context) is constructed from the connectives and a fixed, denumerable set of (formula) variable symbols in the usual way. The corresponding formula algebra is denoted by
of formulas (terms in an algebraic context) is constructed from the connectives and a fixed, denumerable set of (formula) variable symbols in the usual way. The corresponding formula algebra is denoted by 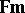 . This is the "absolutely free" algebra of type
. This is the "absolutely free" algebra of type 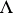 with an
with an  -ary operation
-ary operation 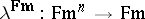 for each
for each 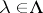 of arity
of arity  such that
such that 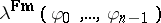 is the formula
is the formula 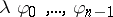 , in prefix notation, or
, in prefix notation, or 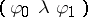 when
when 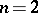 and infix notation is used. The operation of simultaneously substituting fixed but arbitrary formulas for variables is identified with the unique endomorphism of
and infix notation is used. The operation of simultaneously substituting fixed but arbitrary formulas for variables is identified with the unique endomorphism of  it determines. A logistic or deductive system is a pair
it determines. A logistic or deductive system is a pair  , where
, where  , the consequence relation of
, the consequence relation of 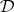 , is a binary relation between sets of formulas and individual formulas satisfying the following well-known conditions: For all
, is a binary relation between sets of formulas and individual formulas satisfying the following well-known conditions: For all 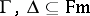 and
and 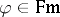 ,
,
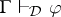 for all
for all 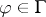 ;
;
 and
and 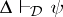 for every
for every 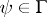 imply
imply 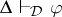 ;
;
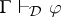 implies
implies 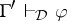 for some finite
for some finite 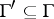 (finiteness);
(finiteness);
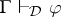 implies
implies 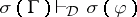 for every substitution
for every substitution 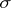 (substitution invariance). Substitution invariance is the technical counterpart of the idea that logical consequence depends on form and not substance. It plays a key role in abstract algebraic logic because it is an essential feature of equational logic.
(substitution invariance). Substitution invariance is the technical counterpart of the idea that logical consequence depends on form and not substance. It plays a key role in abstract algebraic logic because it is an essential feature of equational logic.
A formula 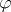 is a theorem of
is a theorem of 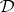 if
if 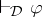 (i.e., it is a consequence of the empty set of formulas). The set of theorems, which may be empty, is denoted by
(i.e., it is a consequence of the empty set of formulas). The set of theorems, which may be empty, is denoted by 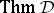 . A set
. A set 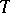 of formulas is a theory of a deductive system
of formulas is a theory of a deductive system 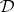 if it is closed under consequence, i.e.,
if it is closed under consequence, i.e., 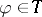 whenever
whenever 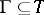 and
and 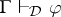 .
. 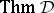 is the smallest theory. The set of all theories of
is the smallest theory. The set of all theories of 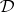 is denoted by
is denoted by 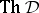 . The theory axiomatized by an arbitrary set
. The theory axiomatized by an arbitrary set 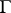 of formulas is the set of all formulas
of formulas is the set of all formulas 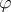 such that
such that 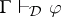 .
.
Deductive systems in this sense include all the familiar sentential logics (cf. also Propositional calculus) together with their various fragments and refinements — for example, the classical and intuitionistic propositional calculi 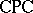 and
and 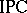 , the intermediate logics (cf. also Intermediate logic), the various modal logics, including
, the intermediate logics (cf. also Intermediate logic), the various modal logics, including 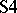 and
and 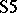 (cf. also Modal logic), and the multiple-valued logics of J. Łukasiewicz and E. Post (cf. also Many-valued logic). The substructural logics, such as BCK logic, relevance logic and linear logic can also be formulated as deductive systems, although they are often formulated as Gentzen-type systems (cf. also Gentzen formal system). Even first-order predicate logic can be formalized as a deductive system, although in its usual formulation it is not substitution-invariant.
(cf. also Modal logic), and the multiple-valued logics of J. Łukasiewicz and E. Post (cf. also Many-valued logic). The substructural logics, such as BCK logic, relevance logic and linear logic can also be formulated as deductive systems, although they are often formulated as Gentzen-type systems (cf. also Gentzen formal system). Even first-order predicate logic can be formalized as a deductive system, although in its usual formulation it is not substitution-invariant.
A (logical) matrix is a structure of the form 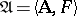 , where
, where 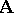 is an algebra (of the same language type as
is an algebra (of the same language type as 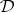 ), the underlying algebra of
), the underlying algebra of 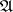 , and
, and 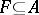 , the designated set of
, the designated set of 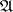 . An interpretation of
. An interpretation of 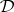 is a matrix
is a matrix 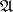 together with a homomorphism
together with a homomorphism 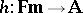 from the algebra of formulas
from the algebra of formulas 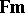 into the underlying algebra of
into the underlying algebra of 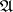 .
. 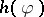 is to be thought of as the "sense" or "meaning" of the formula
is to be thought of as the "sense" or "meaning" of the formula 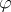 under the interpretation, and
under the interpretation, and 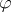 is "true" or "false" depending on whether or not
is "true" or "false" depending on whether or not 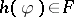 . By the Frege principle, this truth value is the denotation of
. By the Frege principle, this truth value is the denotation of 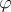 under the interpretation. Truth must be preserved under consequence in the sense that, if
under the interpretation. Truth must be preserved under consequence in the sense that, if 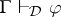 and each
and each 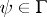 is true under the interpretation, then
is true under the interpretation, then  must also be true. A set
must also be true. A set 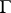 of formulas is said to define a class
of formulas is said to define a class 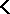 of interpretations if
of interpretations if 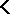 is the class of all interpretations in which each formula of
is the class of all interpretations in which each formula of 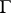 is true. Because truth is preserved under consequence, the theory axiomatized by
is true. Because truth is preserved under consequence, the theory axiomatized by 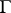 also defines
also defines 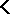 ; it turns out that it is the unique theory with this property.
; it turns out that it is the unique theory with this property.
The formulas 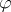 and
and 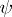 are equivalent over a given class
are equivalent over a given class 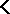 of interpretations (in the Fregean sense) if they have the same truth value, i.e.,
of interpretations (in the Fregean sense) if they have the same truth value, i.e., 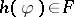 if and only if
if and only if 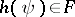 for each
for each 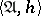 in
in 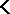 . They are logically equivalent (with respect to
. They are logically equivalent (with respect to 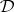 ) if they are equivalent over the class of all interpretations.
) if they are equivalent over the class of all interpretations.
The semantical and logistic approaches diverge at this point. In the former attention is restricted to a specific class of interpretations whose peculiar structure may play an important role in the meta-theory. In contrast, in the logistic method every interpretation is considered, and consequently only its representation as an abstract set with operations and a designated subset is significant. Deduction systems treated in this way are sometimes referred to as uninterpreted.
The foundations of the logistic method in abstract algebraic logic can be found in [a24], [a34]; for more recent work, see [a35]. For relation, polyadic and cylindric algebras, see [a9], [a19], [a22]. For the origin of the notion of a deductive system, see [a33].
Logistic abstract algebraic logic.
The assumption that the deductive system 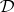 is uninterpreted implies that one need consider only those matrices
is uninterpreted implies that one need consider only those matrices 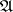 with the property that
with the property that 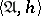 is an interpretation for every
is an interpretation for every 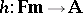 . Such a matrix is called a (matrix) model of
. Such a matrix is called a (matrix) model of 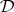 ; the class of all models of
; the class of all models of 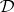 is denoted by
is denoted by 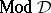 . Secondly, the properties of a given class of interpretations are for most purposes completely specified by the theory that defines it. So matters can be simplified by considering equivalence of formulas over theories rather than classes of interpretations.
. Secondly, the properties of a given class of interpretations are for most purposes completely specified by the theory that defines it. So matters can be simplified by considering equivalence of formulas over theories rather than classes of interpretations.
Two formulas 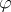 and
and 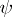 are equivalent over a theory
are equivalent over a theory 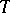 , or
, or 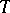 -equivalent, in the Fregean sense, if, for every theory
-equivalent, in the Fregean sense, if, for every theory 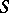 that extends
that extends 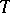 ,
, 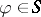 if and only if
if and only if 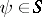 ; the binary relation between formulas defined this way is called the Frege relation of
; the binary relation between formulas defined this way is called the Frege relation of 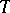 and denoted by
and denoted by 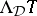 .
. 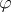 and
and 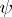 are logically equivalent (with respect to
are logically equivalent (with respect to 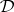 ) if they are equivalent over every theory, or, equivalently, if they are equivalent over
) if they are equivalent over every theory, or, equivalently, if they are equivalent over 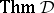 , the set of theorems. In terms of the consequence relation,
, the set of theorems. In terms of the consequence relation,  and
and 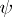 are logically equivalent over
are logically equivalent over 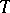 if and only if
if and only if 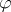 and
and  are each consequences of the other over
are each consequences of the other over 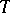 ; symbolically,
; symbolically, 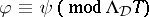 if
if 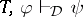 and
and 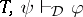 .
.
If, as in the case of the classical and intuitionistic propositional calculi, 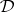 has a binary implication connective
has a binary implication connective  for which the deduction theorem holds, then
for which the deduction theorem holds, then  if and only if
if and only if 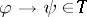 and
and 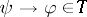 , or equivalently if there is a biconditional,
, or equivalently if there is a biconditional, 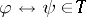 . So, under these rather weak conditions on
. So, under these rather weak conditions on  logical equivalence in the Fregean sense agrees with the familiar definition of the concept.
logical equivalence in the Fregean sense agrees with the familiar definition of the concept.
As a consequence of Frege's principle, the following rule of replacement, or compositionality, holds when 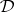 is the classical propositional calculus
is the classical propositional calculus 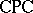 or the intuitionistic propositional calculus
or the intuitionistic propositional calculus 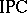 . If in any formula
. If in any formula 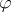 a subformula
a subformula 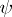 is replaced by an equivalent formula
is replaced by an equivalent formula 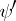 , the resulting formula
, the resulting formula 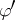 is equivalent to
is equivalent to 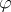 . In algebraic terms this says that for every theory
. In algebraic terms this says that for every theory 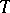 of
of 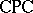 or
or 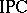 ,
, 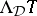 is a congruence relation on the algebra of formulas
is a congruence relation on the algebra of formulas 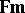 . A deductive system
. A deductive system 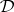 for which
for which 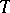 -equivalence is compositional for every theory
-equivalence is compositional for every theory 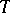 is called Fregean or extensional; non-Fregean systems are called intensional.
is called Fregean or extensional; non-Fregean systems are called intensional.
If 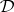 is Fregean, it is possible to form the quotient matrices
is Fregean, it is possible to form the quotient matrices 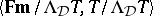 , where
, where 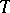 ranges over all theories. These are called the Lindenbaum–Tarski models of
ranges over all theories. These are called the Lindenbaum–Tarski models of 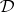 . The construction of the Lindenbaum–Tarski models is more complicated in the case of intensional systems, where the Frege relation is not a congruence relation. For example, for every theory
. The construction of the Lindenbaum–Tarski models is more complicated in the case of intensional systems, where the Frege relation is not a congruence relation. For example, for every theory 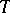 of the strong form of the modal system
of the strong form of the modal system 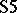 , with necessitation as a rule of inference (see below), one has
, with necessitation as a rule of inference (see below), one has 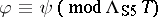 if and only if
if and only if 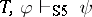 and
and 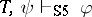 if and only if
if and only if 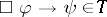 and
and 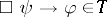 . But this relation is not, in general, compositional.
. But this relation is not, in general, compositional. 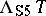 includes however a largest compositional equivalence relation, called the Suszko congruence of
includes however a largest compositional equivalence relation, called the Suszko congruence of 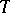 over
over 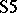 and denoted by
and denoted by 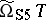 . It can be shown that
. It can be shown that 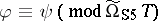 if and only if
if and only if 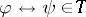 . So
. So 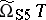 captures the usual notion of
captures the usual notion of 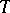 -equivalence for
-equivalence for  .
.
Suszko congruences can be defined for the theories of any deductive system, and consequently one can construct Lindenbaum–Tarski models of any deductive system. But it turns out to be more useful to consider the Lindenbaum–Tarski process in a broader context. A subset 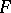 of the underlying set of an algebra
of the underlying set of an algebra 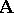 , of the same language type as
, of the same language type as 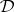 , is called a filter of
, is called a filter of 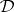 if
if 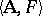 is a model of
is a model of 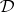 ; thus
; thus 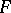 is a filter if and only if it is closed under consequence in the sense that, if
is a filter if and only if it is closed under consequence in the sense that, if 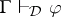 , one has
, one has 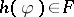 for every
for every 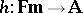 such that
such that 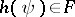 for every
for every 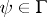 . The set of filters of
. The set of filters of 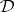 on
on 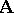 is denoted by
is denoted by 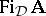 . It is easy to see that the theories are the filters on the formula algebra. The Frege relation and the Suszko congruence generalize to filters on an arbitrary algebra
. It is easy to see that the theories are the filters on the formula algebra. The Frege relation and the Suszko congruence generalize to filters on an arbitrary algebra 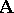 in a natural way. The Frege relation
in a natural way. The Frege relation 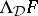 is the set of all pairs
is the set of all pairs 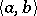 of elements of
of elements of 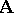 such that, for every filter
such that, for every filter 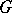 on
on 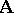 that includes
that includes 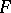 ,
, 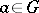 if and only if
if and only if 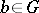 . The Suszko congruence
. The Suszko congruence 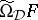 is the largest congruence relation on
is the largest congruence relation on 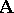 that is included in
that is included in 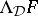 ; it always exists.
; it always exists.
The quotient matrix 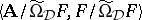 is called the Suszko-reduction of
is called the Suszko-reduction of 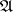 and is denoted by
and is denoted by  . It can be shown that
. It can be shown that  coincides with (or, more precisely, is isomorphic to)
coincides with (or, more precisely, is isomorphic to) 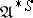 . A model
. A model 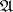 is Suszko-reduced if
is Suszko-reduced if 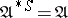 , i.e.,
, i.e., 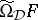 is the identity relation. The class of all Suszko-reduced models of
is the identity relation. The class of all Suszko-reduced models of 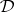 is denoted by
is denoted by 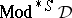 . The Suszko-reduced models of
. The Suszko-reduced models of 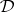 are those for which two elements are equivalent in the Fregean sense if and only if they are identical.
are those for which two elements are equivalent in the Fregean sense if and only if they are identical.
The class of underlying algebras of the Suszko-reduced models of 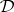 is denoted by
is denoted by  . The underlying algebras of
. The underlying algebras of  are the Boolean algebras. Each filter of
are the Boolean algebras. Each filter of  on a Boolean algebra
on a Boolean algebra 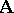 is completely determined by its Suszko congruence
is completely determined by its Suszko congruence 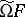 ; more precisely, it coincides with the set of all elements of
; more precisely, it coincides with the set of all elements of 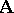 equivalent under
equivalent under 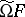 to the unit element
to the unit element 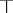 of
of 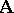 . Moreover, every congruence relation on
. Moreover, every congruence relation on 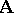 is the Suszko congruence of a filter of
is the Suszko congruence of a filter of 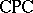 . It follows that the consequence relation of
. It follows that the consequence relation of 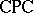 is completely determined by the equational logic of Boolean algebras, and in this way the class of Boolean algebras
is completely determined by the equational logic of Boolean algebras, and in this way the class of Boolean algebras 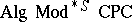 constitutes a complete algebraic semantics for
constitutes a complete algebraic semantics for 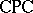 . In a similar way, the class of Heyting algebras
. In a similar way, the class of Heyting algebras 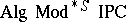 and the class of so-called monadic algebras
and the class of so-called monadic algebras 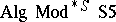 constitute complete algebraic semantics for
constitute complete algebraic semantics for 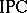 and
and 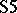 , respectively, and this is the case for almost all the familiar deductive systems. But in general the connection between the consequence relation of a deductive system
, respectively, and this is the case for almost all the familiar deductive systems. But in general the connection between the consequence relation of a deductive system  and the equational logic of
and the equational logic of  is much weaker. A central problem for abstract algebraic logic is the characterization of those deductive systems for which this connection is as strong as for the traditional logics.
is much weaker. A central problem for abstract algebraic logic is the characterization of those deductive systems for which this connection is as strong as for the traditional logics.
Early work on the Suszko and the closely related Leibniz and Tarski congruences discussed below can be found in [a24], [a31]. [a32] contains historical information on the Tarski–Lindenbaum process. The essential idea of Fregean logic as presented here originated with R. Suszko [a4], [a30].
Algebraizable logics.
The basis of the abstract algebraic logic definition of an algebraizable deductive system is the notion of bisimulation between the consequence relation of 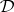 and the equational consequence relation of a class of algebras.
and the equational consequence relation of a class of algebras.
Let 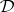 be a deductive system and
be a deductive system and 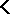 a class of algebras over the same language type. Let
a class of algebras over the same language type. Let
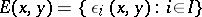 |
be a (possibly infinite) non-empty system of formulas in two variables. 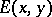 is said to be a faithful interpretation of the equational logic of
is said to be a faithful interpretation of the equational logic of 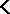 in
in 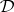 if, for every equation
if, for every equation 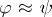 and every set of equations
and every set of equations 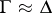 ,
,
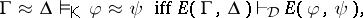 |
where 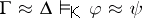 means that
means that 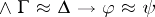 is a quasi-identity of
is a quasi-identity of  . Also,
. Also, 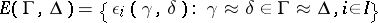 and
and 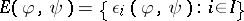 , and
, and 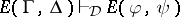 is shorthand for the system of entailments
is shorthand for the system of entailments 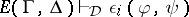 for every
for every 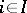 ; "iff" stands for "if and only if" .
; "iff" stands for "if and only if" .
Let
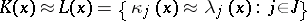 |
be a non-empty system of equations in one variable. 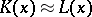 is a faithful interpretation of
is a faithful interpretation of 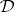 in the equational logic of
in the equational logic of 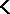 if, for all
if, for all 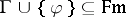 ,
,
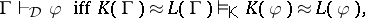 |
where 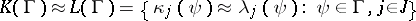 and
and 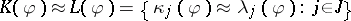 . The two interpretations are mutual inverses if
. The two interpretations are mutual inverses if
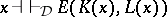 |
and
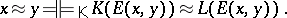 |
A pair of mutually invertible interpretations 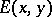 and
and 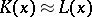 such as these is called a bisimulation between
such as these is called a bisimulation between 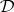 and the equational logic of
and the equational logic of 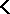 . A deductive system
. A deductive system 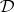 is algebraizable if there is a bisimulation between
is algebraizable if there is a bisimulation between 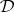 and the equational logic of some class
and the equational logic of some class 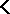 of algebras; it is finitely algebraizable if the interpretations are finite. If
of algebras; it is finitely algebraizable if the interpretations are finite. If 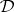 is algebraizable, then
is algebraizable, then 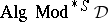 is the largest class
is the largest class 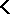 with the above properties; it is called the equivalent algebraic semantics of
with the above properties; it is called the equivalent algebraic semantics of 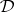 . In general,
. In general,  is not elementary (i.e., definable by a set of sentences of the first-order predicate logic), and in fact it is an elementary class just in case
is not elementary (i.e., definable by a set of sentences of the first-order predicate logic), and in fact it is an elementary class just in case 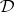 is finitely algebraizable. In this case
is finitely algebraizable. In this case 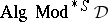 is a quasi-variety (cf. also Quasi-variety)
is a quasi-variety (cf. also Quasi-variety)
The classical and intuitionistic propositional calculi 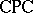 and
and 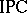 are finitely algebraizable and their equivalent quasi-varieties are, respectively, the varieties
are finitely algebraizable and their equivalent quasi-varieties are, respectively, the varieties 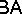 of Boolean algebras and
of Boolean algebras and 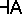 of Heyting algebras. In both cases the faithful interpretation of the equational logic of the equivalent quasi-variety in the deductive system is given by
of Heyting algebras. In both cases the faithful interpretation of the equational logic of the equivalent quasi-variety in the deductive system is given by 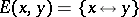 , where
, where  is, respectively, the classical and intuitionistic biconditional, and the inverse faithful interpretation is
is, respectively, the classical and intuitionistic biconditional, and the inverse faithful interpretation is 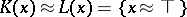 . Most of the deductive systems of traditional algebraic logic are finitely algebraizable with similar interpretations. However, there are finitely algebraizable logics with non-standard interpretations, for example the entailment logic
. Most of the deductive systems of traditional algebraic logic are finitely algebraizable with similar interpretations. However, there are finitely algebraizable logics with non-standard interpretations, for example the entailment logic 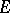 .
.
The bisimulation between a finitely algebraizable deductive system 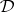 and the equational logic of its equivalent quasi-variety
and the equational logic of its equivalent quasi-variety 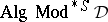 induces a correspondence between the meta-logical properties of
induces a correspondence between the meta-logical properties of 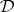 and the algebraic properties of
and the algebraic properties of 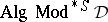 . This correspondence has been the focus of considerable attention in abstract algebraic logic. One of the most important aspects of traditional algebraic logic is the way in which it can be used to reformulate meta-logical properties of a particular logical system in algebraic terms. Abstract algebraic logic provides a framework for studying such correspondences in a general context. Known meta-logical or algebraic results can then be applied to obtain new results in the other domain. Some correspondences of this kind that have been established are between:
. This correspondence has been the focus of considerable attention in abstract algebraic logic. One of the most important aspects of traditional algebraic logic is the way in which it can be used to reformulate meta-logical properties of a particular logical system in algebraic terms. Abstract algebraic logic provides a framework for studying such correspondences in a general context. Known meta-logical or algebraic results can then be applied to obtain new results in the other domain. Some correspondences of this kind that have been established are between:
meta-logical interpolation and algebraic amalgamation, e.g., the Craig interpolation theorem of 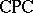 and the amalgamation property of
and the amalgamation property of 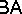 ;
;
definability (in the sense of the Beth definability theorem of first-order predicate logic) and the property that every epimorphism (in the categorical sense) is surjective;
the deduction theorem and the equational definability of principal congruences. The deduction theorem is the formal expression of one of the most important and useful properties of classical logic: to prove that an implication holds between propositions it suffices to give a proof of the conclusion on the basis of the assumption of the antecedent. It is such a familiar part of ordinary logical argumentation that it is hardly recognizable as being something whose use might be problematic. But in fact it is not part of the usual formalizations of 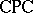 and must be proved as a meta-theorem. Moreover, while the deduction theorem remains valid for intuitionistic logic, it is known to fail in other important logics, for instance, certain systems of modal logic. It turns out that there is a close connection between the deduction theorem and the universal algebraic notion of definable principal congruence relations. The development of abstract algebraic logic was motivated in part by a desire to provide the proper context in which to formalize this connection precisely. The ultimate goal was to be able to apply the extensive work on the definability of principal congruence relations in universal algebra to answer some important questions about the validity of the deduction theorem in a variety of logical systems.
and must be proved as a meta-theorem. Moreover, while the deduction theorem remains valid for intuitionistic logic, it is known to fail in other important logics, for instance, certain systems of modal logic. It turns out that there is a close connection between the deduction theorem and the universal algebraic notion of definable principal congruence relations. The development of abstract algebraic logic was motivated in part by a desire to provide the proper context in which to formalize this connection precisely. The ultimate goal was to be able to apply the extensive work on the definability of principal congruence relations in universal algebra to answer some important questions about the validity of the deduction theorem in a variety of logical systems.
Let 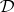 be a deductive system. A finite non-empty set
be a deductive system. A finite non-empty set 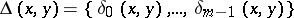 of binary formulas is called a deduction-detachment system for
of binary formulas is called a deduction-detachment system for 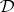 if the following equivalence holds for all
if the following equivalence holds for all 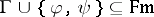 :
:
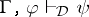 |
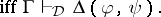 |
A deductive system has the deduction-detachment theorem if it has a deduction-detachment system. The implication 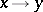 forms a singleton deduction-detachment system for
forms a singleton deduction-detachment system for 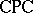 and
and 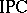 , while the formula
, while the formula 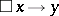 forms a singleton deduction-detachment system for the modal systems
forms a singleton deduction-detachment system for the modal systems 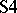 and
and 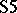 .
.
For an algebra 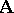 , let
, let 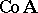 be the set of all congruences of
be the set of all congruences of 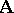 . If
. If 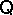 is a quasi-variety, then a congruence
is a quasi-variety, then a congruence 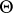 on an arbitrary algebra
on an arbitrary algebra 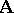 (not necessarily in
(not necessarily in 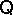 ) is called a
) is called a 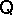 -congruence if
-congruence if 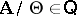 . If
. If 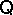 is a variety (cf. also Algebraic systems, variety of) and
is a variety (cf. also Algebraic systems, variety of) and 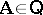 , then every congruence is a
, then every congruence is a 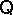 -congruence. The principal
-congruence. The principal 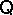 -congruence generated by the pair
-congruence generated by the pair  and
and 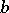 ,
, 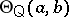 , is the smallest
, is the smallest 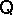 -congruence that identifies
-congruence that identifies  and
and 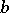 . A quasi-variety
. A quasi-variety 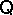 has equationally definable principal relative congruences (EDPRC) if there is a finite system of equations
has equationally definable principal relative congruences (EDPRC) if there is a finite system of equations 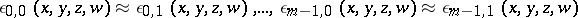 , in four variables, such that, for every
, in four variables, such that, for every 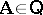 and all
and all 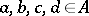 ,
,
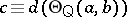 |
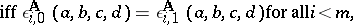 |
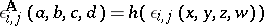 , where
, where 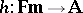 is any homomorphism such that
is any homomorphism such that 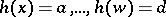 .
.
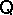 -congruence generation in the formula algebra can be interpreted as the consequence relation of the equational logic of
-congruence generation in the formula algebra can be interpreted as the consequence relation of the equational logic of 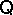 . Thus, if
. Thus, if 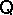 has EDPRC, the defining equations
has EDPRC, the defining equations 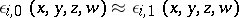 can be interpreted collectively as an implication connective for the equational logic. This observation is reflected in the following theorem: Let
can be interpreted collectively as an implication connective for the equational logic. This observation is reflected in the following theorem: Let 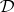 be a finitely algebraizable deductive system and let
be a finitely algebraizable deductive system and let 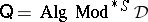 be its equivalent quasi-variety. Then
be its equivalent quasi-variety. Then 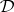 has the deduction-detachment theorem if and only if
has the deduction-detachment theorem if and only if 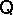 has EDPRC.
has EDPRC.
A correspondence of this kind makes it possible to infer new metalogical properties from known algebraic ones and vice versa. In this way it can be proved that orthomodular logic does not have the deduction-detachment theorem. Orthomodular logic can be viewed as a finitely algebraizable deductive system whose equivalent quasi-variety is the variety of orthomodular lattices. There are several different deductive systems that fit this description. It can be shown that, if a quasi-variety  has EDPRC, then it has the relative congruence extension property. The variety of orthomodular lattices does not have this property. Thus, no orthomodular logic of the kind described above can have the deduction-detachment theorem with respect to any system of binary formulas.
has EDPRC, then it has the relative congruence extension property. The variety of orthomodular lattices does not have this property. Thus, no orthomodular logic of the kind described above can have the deduction-detachment theorem with respect to any system of binary formulas.
A definition of an abstract class of deductive systems with the algebraic properties of the traditional logics was first proposed in [a6]; earlier definitions, notably that in [a28], were not truly abstract because they relied on the existence of connectives with special properties. The notion of algebraizability was subsequently extended in several ways ([a14], [a10], [a21], [a20]). For entailment logic and its algebraizability, see [a1], [a6]. For the deduction theorem in abstract algebraic logic, see [a5], [a11]. The result on orthomodular logic is found in [a37], [a25].
The algebraic hierarchy.
Finitely algebraizable deductive systems exhibit the strongest connection between the meta-logical properties of 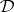 and the algebraic properties of
and the algebraic properties of 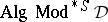 . But there are deductive systems where the connection is not as strong but which still have a clear algebraic character. One of the goals of abstract algebraic logic is the classification of deductive systems of this kind. This leads to a hierarchy of systems with the finitely algebraizable systems at the top. There are several ways of specifying it. The most natural, in view of the definition of algebraizability, is in terms of progressively weaker notions of bisimulation. The characteristic property of all deductive systems that make up the hierarchy is that equivalence, as expressed by the Suszko congruence, is explicitly definable in some way. The classification of the hierarchy is based on the nature of the definition.
. But there are deductive systems where the connection is not as strong but which still have a clear algebraic character. One of the goals of abstract algebraic logic is the classification of deductive systems of this kind. This leads to a hierarchy of systems with the finitely algebraizable systems at the top. There are several ways of specifying it. The most natural, in view of the definition of algebraizability, is in terms of progressively weaker notions of bisimulation. The characteristic property of all deductive systems that make up the hierarchy is that equivalence, as expressed by the Suszko congruence, is explicitly definable in some way. The classification of the hierarchy is based on the nature of the definition.
Let 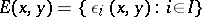 be a (possibly infinite) set of formulas in two variables.
be a (possibly infinite) set of formulas in two variables. 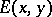 is a proto-equivalence system for a deductive system
is a proto-equivalence system for a deductive system 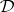 if
if
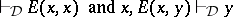 |
(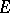 -detachment).
-detachment).
A non-empty proto-equivalence system 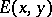 is an equivalence system if
is an equivalence system if
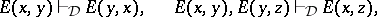 |
and
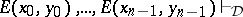 |
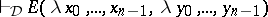 |
for all 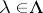 (
( is the rank of
is the rank of 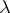 ). The reflexivity and transitivity axioms are superfluous as they are provable from the remaining conditions.
). The reflexivity and transitivity axioms are superfluous as they are provable from the remaining conditions.
The connection between equivalence systems and the Suszko congruence is expressed in the following theorem: A non-empty system 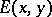 of formulas in two variables is an equivalence system for a deductive system
of formulas in two variables is an equivalence system for a deductive system 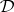 if and only if it defines Suszko congruences in the sense that, for every algebra
if and only if it defines Suszko congruences in the sense that, for every algebra 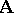 and
and 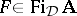 ,
,
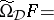 |
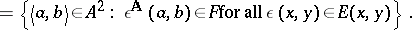 |
A deductive system is protoalgebraic if it has a proto-equivalence system. Every proto-equivalence system includes a finite subset that is also a proto-equivalence system. A deductive system is (finitely) equivalential if it has a (finite) equivalence system.
The formulas that faithfully interpret in a (finitely) algebraizable deductive system the equational logic of its equivalent algebraic semantics form a (finite) equivalence system. This leads to a meta-logical characterization theorem of (finitely) algebraizable deductive systems that is intrinsic in the sense that it does not require a priori knowledge of the equivalent algebraic semantics: A deductive system is (finitely) algebraizable if and only if it has a (finite) equivalence system for which there exists a finite system 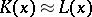 of equations in one variable, called a system of defining equations, such that
of equations in one variable, called a system of defining equations, such that 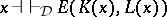 .
.
This last condition abstracts an important property of the biconditional  of both classical and intuitionistic propositional logic, namely, that
of both classical and intuitionistic propositional logic, namely, that  and the biconditional
and the biconditional 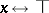 are interderivable.
are interderivable.
The protoalgebraic, (finitely) equivalential and (finitely) algebraizable deductive systems constitute, along with the weakly algebraizable systems discussed shortly, the algebraic hierarchy. Natural deductive systems can be found to separate all levels of the hierarchy. Protoalgebraicity is a very weak condition and almost all known deductive systems have the property. There are some that do not however, for example the conjunction/disjunction fragment of 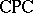 , subintuitionistic logics and Belnap's logic. Almost all the weak modal logics, without necessitation as a rule of inference, are protoalgebraic but not equivalential. There are also examples of algebraizable logics that are not finitely equivalential, and hence also of logics that are equivalential but not finitely equivalential.
, subintuitionistic logics and Belnap's logic. Almost all the weak modal logics, without necessitation as a rule of inference, are protoalgebraic but not equivalential. There are also examples of algebraizable logics that are not finitely equivalential, and hence also of logics that are equivalential but not finitely equivalential.
In addition to the syntactical characterizations considered above, each level of the hierarchy can be characterized by both algebraic and model-theoretic means. The algebraic characterization makes use of the Leibniz congruence, a more primitive but more manageable variant of the Suszko congruence.
Given any algebra 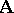 and any subset
and any subset 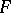 of
of 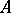 , there is a largest congruence relation
, there is a largest congruence relation 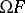 on
on 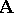 compatible with
compatible with 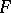 in the sense that
in the sense that 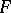 is a union of equivalence classes of
is a union of equivalence classes of 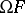 .
. 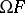 is called the Leibniz congruence of
is called the Leibniz congruence of 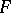 . The relationship between the Leibniz and Suszko congruences is straightforward: For every deductive system
. The relationship between the Leibniz and Suszko congruences is straightforward: For every deductive system 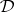 and
and 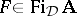 ,
,
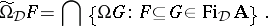 |
 and
and 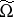 can both be viewed as operators mapping the lattice of
can both be viewed as operators mapping the lattice of 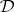 -filters of
-filters of 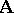 to the lattice of congruences of
to the lattice of congruences of 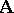 . Note that the Leibniz and Suszko congruences coincide on
. Note that the Leibniz and Suszko congruences coincide on 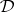 -filters just in case the Leibniz operator is order-preserving, i.e.,
-filters just in case the Leibniz operator is order-preserving, i.e., 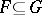 implies
implies 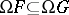 for all
for all 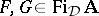 .
.
Let 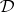 be a deductive system. Then the following characterizations hold:
be a deductive system. Then the following characterizations hold:
i) 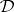 is protoalgebraic if and only if the Leibniz operator
is protoalgebraic if and only if the Leibniz operator  is order-preserving, i.e., if and only if the Leibniz and Suszko congruences coincide;
is order-preserving, i.e., if and only if the Leibniz and Suszko congruences coincide;
ii) 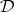 is equivalential if and only if it is protoalgebraic and
is equivalential if and only if it is protoalgebraic and  commutes with inverse homomorphic images; more precisely,
commutes with inverse homomorphic images; more precisely, 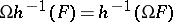 for every homomorphism
for every homomorphism 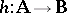 and every
and every 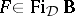 ;
;
iii) 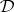 is finitely equivalential if and only if it is protoalgebraic and
is finitely equivalential if and only if it is protoalgebraic and  commutes with directed unions; more precisely,
commutes with directed unions; more precisely, 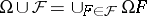 for every
for every 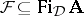 that is upward-directed by inclusion;
that is upward-directed by inclusion;
iv) 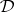 is algebraizable if and only if it is equivalential and
is algebraizable if and only if it is equivalential and  is injective;
is injective;
v) 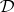 is finitely algebraizable if and only if it is finitely equivalential and
is finitely algebraizable if and only if it is finitely equivalential and  is injective.
is injective.
A deductive system 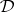 is said to be weakly algebraizable if it is protoalgebraic and the Leibniz operator
is said to be weakly algebraizable if it is protoalgebraic and the Leibniz operator  is injective. A syntactical characterization of weak algebraizability is also known.
is injective. A syntactical characterization of weak algebraizability is also known.
Calculation of the Leibniz congruences can be a practical matter for some small algebras. This gives a way of verifying that a deductive system is not finitely algebraizable, or that a quasi-variety is not the equivalent algebraic semantics of any deductive system. This method has been used to show that the relevance logic 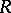 and the various formalizations of modal logic without the rule of necessitation are not finitely algebraizable. It has also been used to show that the variety of complemented distributive lattices is not the equivalent algebraic semantics of any deductive system.
and the various formalizations of modal logic without the rule of necessitation are not finitely algebraizable. It has also been used to show that the variety of complemented distributive lattices is not the equivalent algebraic semantics of any deductive system.
There is also a model-theoretic characterization of the algebraic hierarchy similar to the well-known model-theoretic characterizations of equational and quasi-equational classes by G. Birkhoff and A. Mal'cev.
The Leibniz-reduction of a model of a deductive system is defined just like the Suszko-reduction, except that the Leibniz congruence is used in place of the Suszko congruence. 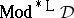 denotes the class of all Leibniz-reduced models of
denotes the class of all Leibniz-reduced models of 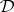 . If
. If 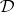 is protoalgebraic, then
is protoalgebraic, then 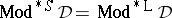 ; this equality in fact characterizes protoalgebraic systems. In general, the best one has is that
; this equality in fact characterizes protoalgebraic systems. In general, the best one has is that 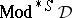 coincides with the class of all matrices isomorphic to a subdirect product of matrices in
coincides with the class of all matrices isomorphic to a subdirect product of matrices in 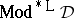 , in symbols
, in symbols  .
.
For any class 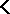 of matrices,
of matrices, 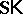 ,
, 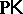 ,
, 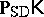 , and
, and 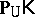 denote, respectively, the classes of isomorphic images of submatrices, direct products, subdirect products, and ultraproducts of members of
denote, respectively, the classes of isomorphic images of submatrices, direct products, subdirect products, and ultraproducts of members of 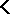 .
.
Let 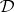 be a deductive system. Then the following characterizations hold:
be a deductive system. Then the following characterizations hold:
a) 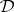 is protoalgebraic if and only if
is protoalgebraic if and only if 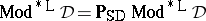 , i.e.,
, i.e., 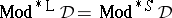 ;
;
b) 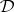 is equivalential if and only if
is equivalential if and only if 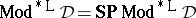 ;
;
c) 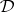 is finitely equivalential if and only if
is finitely equivalential if and only if 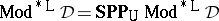 , i.e.,
, i.e., 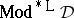 is a quasi-variety in the sense of Mal'cev;
is a quasi-variety in the sense of Mal'cev;
d) 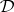 is algebraizable if and only if it is equivalential and
is algebraizable if and only if it is equivalential and 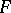 is the minimal
is the minimal 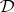 -filter of
-filter of 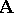 for each
for each 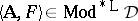 ;
;
e) 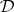 is finitely algebraizable if and only if it is finitely equivalential and
is finitely algebraizable if and only if it is finitely equivalential and 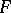 is the minimal
is the minimal 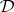 -filter of
-filter of 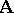 for each
for each 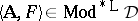 .
.
For papers on the specific levels of the algebraic hierarchy, see [a7], [a6], [a13], [a10], [a21], [a20]. Two references of a more general nature are [a8], [a12].
Protoalgebraic logics.
Within the context of the model theory of first-order logic, a deductive system can be viewed as a strict universal Horn theory with a single unary predicate and without equality. (cf. also Horn clauses, theory of). It is an interesting question as to how much of the model theory of strict universal Horn logic with equality can be recovered by means of the abstract Lindenbaum–Tarski process. In the case of finitely algebraizable deductive systems it can be essentially completely recovered already in the algebraic reducts of the Leibniz-reduced models. The same is true for finitely equivalential systems where the finite equivalence systems give a strong representation of equality, but here the filter part of the Leibniz-reduced model is essential and cannot be discarded. But much can be recovered even in the case of protoalgebraic systems where the proto-equivalence systems give a much weaker representation of equality. Protoalgebraic systems turn out to be the largest class of deductive systems 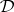 whose Leibniz-reduced model class
whose Leibniz-reduced model class 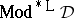 is well behaved in the sense of strict Horn logic with equality, and the key to this is the following correspondence theorem for
is well behaved in the sense of strict Horn logic with equality, and the key to this is the following correspondence theorem for 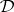 -filters that mirrors the correspondence theorem for congruences in universal algebra: Let
-filters that mirrors the correspondence theorem for congruences in universal algebra: Let 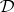 be a protoalgebraic deductive system, and let
be a protoalgebraic deductive system, and let 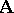 and
and 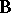 be algebras and
be algebras and 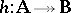 a surjective homomorphism. Finally, let
a surjective homomorphism. Finally, let 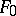 be the smallest
be the smallest 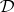 -filter on
-filter on 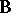 . Then the mapping
. Then the mapping 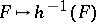 is a one-to-one correspondence between the
is a one-to-one correspondence between the 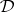 -filters on
-filters on 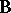 and the
and the  -filters on
-filters on 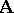 that include
that include  .
.
When 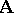 is taken to be
is taken to be  , the algebra of formulas, this correspondence establishes a close connection between the meta-logical properties of
, the algebra of formulas, this correspondence establishes a close connection between the meta-logical properties of 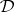 and the algebraic properties of the class
and the algebraic properties of the class 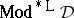 of Leibniz-reduced models of
of Leibniz-reduced models of 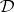 .
.
Every class 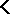 of matrices over the same language type
of matrices over the same language type 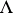 defines a deductive system
defines a deductive system 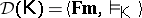 over
over 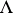 in the following way.
in the following way. 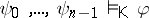 if, for every
if, for every 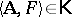 and every homomorphism
and every homomorphism 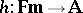 ,
, 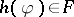 whenever
whenever 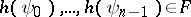 . The following theorem is a generalization of Mal'cev's well-known characterization of the strict universal Horn class generated by an arbitrary class of matrices: Let
. The following theorem is a generalization of Mal'cev's well-known characterization of the strict universal Horn class generated by an arbitrary class of matrices: Let 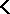 be a class of Leibniz-reduced matrices over the same language type; then
be a class of Leibniz-reduced matrices over the same language type; then
if 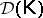 is protoalgebraic, then
is protoalgebraic, then 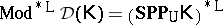 ;
;
if 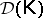 is equivalential, then
is equivalential, then 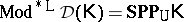 .
.
The following theorem is an analogue of the finite basis theorem of K. Baker for congruence-distributive varieties and of the corresponding result for relatively congruence-distributive quasi-varieties. It uses the notion of filter-distributive deductive system. A deductive system  is filter-distributive if
is filter-distributive if  is a distributive lattice for every algebra
is a distributive lattice for every algebra 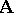 .
.
Let 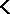 be a finite set of matrices. If
be a finite set of matrices. If 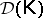 is protoalgebraic and filter-distributive, then
is protoalgebraic and filter-distributive, then 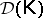 has a presentation by a finite set of axioms and inference rules [a27]. An important related axiomatizability result can be found in [a38].
has a presentation by a finite set of axioms and inference rules [a27]. An important related axiomatizability result can be found in [a38].
In analogy to the algebraic hierarchy there is a classification of deductive systems in terms of progressively weaker versions of a deductive-detachment system. Again protoalgebraic systems lie at the lowest level, and filter-distributive systems constitute another level of hierarchy. See [a11], [a12].
The generalization of Mal'cev's theorem above is one of many model-theoretic theorems of this kind involving various levels of the algebraic hierarchy, and the scope of the theory has been broadened to include infinitary universal Horn logic without equality [a8], [a13], [a15], [a17], [a16].
Second-order algebraizable logics.
There are deductive systems with clear algebraic counterparts that are not protoalgebraic and hence not amenable to the methods of abstract algebraic logic discussed so far. Many examples of this kind arise as fragments of more expressive deductive systems that are finitely algebraizable. A paradigm for deductive systems of this kind is the conjunction/disjunction fragment 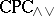 of classical propositional logic. It has a natural algebraic semantics, the variety
of classical propositional logic. It has a natural algebraic semantics, the variety 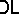 of distributive lattices. In order to extend the standard theory of algebraizability to a wider class of deductive systems, recent investigations in abstract algebraic logic have switched focus from
of distributive lattices. In order to extend the standard theory of algebraizability to a wider class of deductive systems, recent investigations in abstract algebraic logic have switched focus from 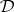 -filters to certain special classes of
-filters to certain special classes of 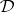 -filters and to a natural generalization of the Leibniz congruence that applies to classes of
-filters and to a natural generalization of the Leibniz congruence that applies to classes of 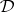 -filters.
-filters.
The non-algebraizability of 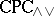 is reflected in the fact that, for an arbitrary algebra
is reflected in the fact that, for an arbitrary algebra 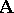 , the Leibniz operator does not give a one-one correspondence between (
, the Leibniz operator does not give a one-one correspondence between (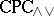 )-filters and
)-filters and 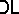 -congruences. The correspondence can in a sense be recovered by replacing single (
-congruences. The correspondence can in a sense be recovered by replacing single (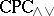 )-filters by sets of (
)-filters by sets of (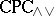 )-filters, each of which is of the form
)-filters, each of which is of the form 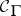 , where
, where 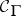 consists of all (
consists of all (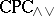 )-filters that are compatible with each member of a fixed but arbitrary class
)-filters that are compatible with each member of a fixed but arbitrary class  of congruences on
of congruences on  . The set of congruences
. The set of congruences 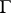 is completely arbitrary, but it turns out that there is always a single congruence
is completely arbitrary, but it turns out that there is always a single congruence 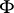 such that
such that 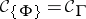 , and in fact a smallest one with this property, and it is necessarily a
, and in fact a smallest one with this property, and it is necessarily a 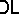 -congruence. Moreover, all
-congruence. Moreover, all 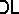 -congruences can be obtained this way.
-congruences can be obtained this way.
Considerations such as these lead to the following notion. A full second-order filter of 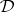 on an algebra
on an algebra 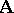 is the set of all
is the set of all 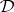 -filters
-filters 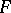 on
on 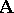 such that
such that 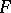 is compatible with a fixed but arbitrary set of congruences. The set of full second-order filters on
is compatible with a fixed but arbitrary set of congruences. The set of full second-order filters on 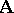 is denoted by
is denoted by 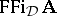 . It is easy to check that every
. It is easy to check that every 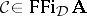 is an algebraic closed-set system of the universe
is an algebraic closed-set system of the universe 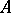 of
of 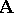 . For each
. For each 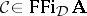 the Frege relation
the Frege relation  is the largest binary relation on
is the largest binary relation on 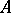 (necessarily an equivalence relation) that is compatible with each
(necessarily an equivalence relation) that is compatible with each 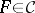 , and the second-order Leibniz congruence, also called the Tarski congruence,
, and the second-order Leibniz congruence, also called the Tarski congruence, 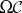 is the largest congruence of
is the largest congruence of  included in
included in 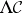 .
.
A set 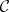 of
of 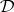 -filters on
-filters on 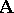 is a full second-order filter of
is a full second-order filter of 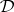 if and only if the set of quotient filters
if and only if the set of quotient filters 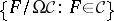 coincides with the set of all
coincides with the set of all 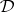 -filters on the quotient algebra
-filters on the quotient algebra 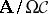 . A full second-order model of
. A full second-order model of 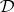 is a second-order matrix
is a second-order matrix 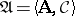 where
where 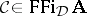 .
. 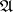 is Leibniz reduced if
is Leibniz reduced if 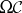 is the identity relation.
is the identity relation. 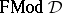 (respectively,
(respectively, 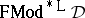 ) is the class of all (Leibniz-reduced) full second-order models of
) is the class of all (Leibniz-reduced) full second-order models of 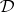 .
.
The following assertion generalizes iv) above, the lattice isomorphism characterization of algebraizable deductive systems, and applies to all deductive systems.
For any deductive system 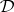 and any algebra
and any algebra 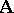 the second-order Leibniz operator
the second-order Leibniz operator  is a dual order-isomorphism between
is a dual order-isomorphism between 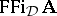 and
and 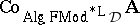 , both partially ordered by set inclusion.
, both partially ordered by set inclusion.
A full second-order model, and more generally, any second-order matrix 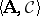 where
where  is an algebraic closed-set system on
is an algebraic closed-set system on 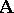 , can be naturally thought of as a model of a Gentzen system. In the context of abstract algebraic logic a Gentzen system can be viewed as a finitary and substitution-invariant consequence relation between sequents; a sequent is a syntactical expression of the form
, can be naturally thought of as a model of a Gentzen system. In the context of abstract algebraic logic a Gentzen system can be viewed as a finitary and substitution-invariant consequence relation between sequents; a sequent is a syntactical expression of the form 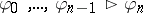 , where
, where 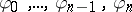 is any finite, non-empty sequence of formulas. Let
is any finite, non-empty sequence of formulas. Let 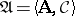 be a second-order matrix, and let
be a second-order matrix, and let 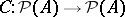 be the closure operator on
be the closure operator on 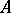 associated with the algebraic closed-set system
associated with the algebraic closed-set system 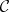 .
. 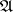 is a model of a Gentzen system
is a model of a Gentzen system 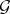 if the following holds. For every entailment
if the following holds. For every entailment
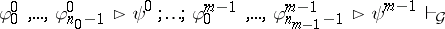 |
 |
and every homomorphism 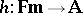 , if
, if  for each
for each 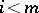 , then
, then 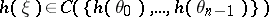 .
.
A deductive system 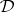 is said to have a fully adequate Gentzen system if the class of full second-order models of
is said to have a fully adequate Gentzen system if the class of full second-order models of 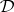 is the class of models of a Gentzen system. (Strictly speaking, this is the form the definition takes when
is the class of models of a Gentzen system. (Strictly speaking, this is the form the definition takes when 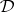 has at least one theorem. The definition together with the formulation of some of the results stated below must be modified slightly if there are no theorems.)
has at least one theorem. The definition together with the formulation of some of the results stated below must be modified slightly if there are no theorems.)
The notion of finite algebraizability for deductive systems can be extended to Gentzen systems in a straightforward way. Just as in the case of deductive systems, if a Gentzen system 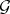 is finitely algebraizable, there is a unique quasi-variety
is finitely algebraizable, there is a unique quasi-variety 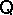 that is equivalent to
that is equivalent to 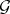 in the sense that there is a bisimulation between the consequence relation of
in the sense that there is a bisimulation between the consequence relation of 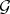 (between sequents) and the equational consequence relation of
(between sequents) and the equational consequence relation of 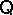 . In view of the above observations it is natural to take a deductive system
. In view of the above observations it is natural to take a deductive system 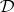 to be second-order finitely algebraizable if it has a fully adequate Gentzen system
to be second-order finitely algebraizable if it has a fully adequate Gentzen system 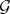 such that
such that 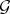 is finitely algebraizable. In this case,
is finitely algebraizable. In this case, 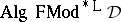 turns out to coincide with the equivalent quasi-variety of
turns out to coincide with the equivalent quasi-variety of 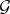 , and the consequence relation of
, and the consequence relation of 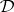 is definable (as part of the consequence relation of
is definable (as part of the consequence relation of 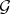 ) in the equational consequence relation of
) in the equational consequence relation of 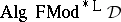 , but not vice versa unless
, but not vice versa unless  is also finitely algebraizable. In the latter case
is also finitely algebraizable. In the latter case 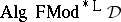 coincides with the equivalent quasi-variety of
coincides with the equivalent quasi-variety of 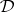 . When
. When 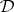 is second-order finitely algebraizable,
is second-order finitely algebraizable, 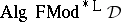 is called the second-order equivalent quasi-variety of
is called the second-order equivalent quasi-variety of 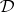 .
.
Strictly speaking, second-order finite algebraizability does not generalize (first-order) finite algebraizability since there are deductive systems that are finitely algebraizable but do not have a fully adequate Gentzen system. However, this new notion of algebraizability goes a long way toward settling some important questions left open by the earlier theory.
One of these deals with the notion of strong finite algebraizability. A finitely algebraizable deductive system is strongly finitely algebraizable if its equivalent quasi-variety is a variety. All the familiar deductive systems of algebraic logic, including both the Fregean and intensional ones, turn out to be strongly finitely algebraizable, but the standard theory is unable to account for this.
Self-extensionality is a much weakened form of the property of being Fregean. A deductive system 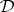 is self-extensional if
is self-extensional if 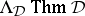 is a congruence relation on the formula algebra.
is a congruence relation on the formula algebra.
Let 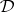 be a self-extensional deductive system that has either conjunction or the deduction-detachment theorem with a single deduction-detachment formula. Then
be a self-extensional deductive system that has either conjunction or the deduction-detachment theorem with a single deduction-detachment formula. Then 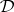 is second-order finitely algebraizable and its second-order equivalent quasi-variety
is second-order finitely algebraizable and its second-order equivalent quasi-variety 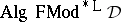 is actually a variety.
is actually a variety.
The conjunction/disjunction fragment 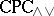 of classical propositional calculus is self-extensional (in fact Fregean) with conjunction. Hence it is finitely algebraizable in the second-order (but not the first-order) sense. Its second-order equivalent quasi-variety
of classical propositional calculus is self-extensional (in fact Fregean) with conjunction. Hence it is finitely algebraizable in the second-order (but not the first-order) sense. Its second-order equivalent quasi-variety 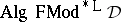 is the variety
is the variety 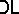 of distributive lattices.
of distributive lattices.
The modal logic 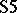 can be formulated as a deductive system in two ways, both of which have the same set of theorems. The first and more familiar one, the strong form, is denoted by
can be formulated as a deductive system in two ways, both of which have the same set of theorems. The first and more familiar one, the strong form, is denoted by 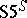 and has the necessitation rule
and has the necessitation rule
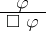 |
as an inference rule (cf. also Permissible law (inference)) along with modus ponens
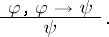 |
The weak form, 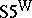 , has modus ponens as its only rule of inference.
, has modus ponens as its only rule of inference. 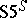 is finitely algebraizable but not self-extensional.
is finitely algebraizable but not self-extensional. 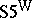 is not algebraizable, but it is self-extensional and has both conjunction and the deduction-detachment theorem with a single deduction-detachment formula. So
is not algebraizable, but it is self-extensional and has both conjunction and the deduction-detachment theorem with a single deduction-detachment formula. So 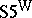 is second-order finitely algebraizable. Moreover, its generalized equivalent quasi-variety is a variety; this turns out to be the variety of monadic algebras, which is also the equivalent quasi-variety of
is second-order finitely algebraizable. Moreover, its generalized equivalent quasi-variety is a variety; this turns out to be the variety of monadic algebras, which is also the equivalent quasi-variety of  .
.
The main source for this section is [a18], where references to other relevant sources can be found. The generalization of algebraizability to Gentzen systems is found in [a29].
Semantics-based abstract algebraic logic.
In this important branch of abstract algebraic logic the fine structure of the interpretations of a deductive system is taken into account. It also features a refinement of the notion of language. Let  be a language type, assumed to be fixed. For an arbitrary set
be a language type, assumed to be fixed. For an arbitrary set  disjoint from
disjoint from 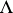 , let
, let 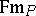 be the set of formulas built up from the elements of
be the set of formulas built up from the elements of 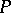 , thought of as abstract atomic formulas, using the connectives of
, thought of as abstract atomic formulas, using the connectives of 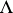 ; the associated formula algebra is denoted by
; the associated formula algebra is denoted by  . For each set
. For each set  of atomic formulas, let
of atomic formulas, let 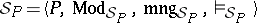 be a four-tuple, where
be a four-tuple, where 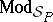 is a class, called the class of models of
is a class, called the class of models of 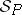 ;
; 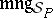 is a function that assigns to each
is a function that assigns to each 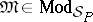 a function
a function 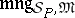 with domain
with domain  , called the meaning function for
, called the meaning function for 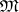 ; and
; and 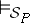 is a binary relation between
is a binary relation between 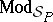 and
and 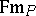 , called the validity relation.
, called the validity relation.
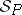 is a semantical system if the following conditions hold for every model
is a semantical system if the following conditions hold for every model  :
:
the meaning of a formula does not change if a subformula is replaced by one with the same meaning, i.e., 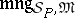 is a homomorphism;
is a homomorphism;
the validity of a formula depends only on its meaning, i.e., if 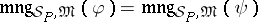 , then
, then 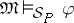 if and only if
if and only if 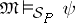 . The meaning algebra of
. The meaning algebra of 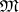 , in symbols
, in symbols  , is the image of
, is the image of  under the meaning homomorphism
under the meaning homomorphism 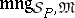 . The final defining condition of a semantical system is the following:
. The final defining condition of a semantical system is the following:
every homomorphism from the formula algebra into the meaning algebra of  is the meaning function of some model, i.e., if
is the meaning function of some model, i.e., if 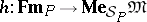 , then there is a
, then there is a  such that
such that 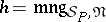 .
.
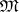 is a model of a set
is a model of a set 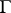 of formulas if
of formulas if 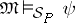 for each
for each 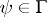 . The class of all models of
. The class of all models of 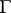 is
is 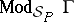 . The consequence relation of
. The consequence relation of 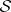 is the relation
is the relation 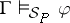 that holds between a set of formulas
that holds between a set of formulas 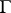 and an individual formula if
and an individual formula if 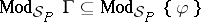 .
. 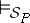 satisfies all the conditions of a consequence relation of a deductive system except possibly finiteness; however, most of the familiar semantical systems are finitary.
satisfies all the conditions of a consequence relation of a deductive system except possibly finiteness; however, most of the familiar semantical systems are finitary. 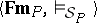 is called the underlying deductive system of
is called the underlying deductive system of 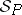 and is denoted by
and is denoted by 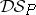 .
.
The theory of a model 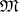 of
of 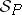 , in symbols
, in symbols 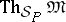 , is the set of all formulas valid in
, is the set of all formulas valid in 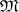 . The truth filter of
. The truth filter of 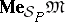 ,
, 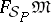 , is the image of
, is the image of 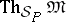 under
under 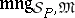 . Because the validity of a formula depends only on its meaning, the meaning matrix
. Because the validity of a formula depends only on its meaning, the meaning matrix 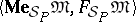 together with the meaning function
together with the meaning function 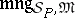 is an interpretation of the underlying deductive system of
is an interpretation of the underlying deductive system of 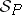 . As before, the Leibniz reduction of the meaning matrix by the Leibniz congruence of the truth filter,
. As before, the Leibniz reduction of the meaning matrix by the Leibniz congruence of the truth filter, 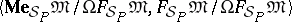 , is denoted by
, is denoted by 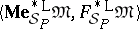 . The model-theoretic properties of a large class of different logical systems can be studied algebraically in this context. Consider, for example, the relation of elementary equivalence. Two models
. The model-theoretic properties of a large class of different logical systems can be studied algebraically in this context. Consider, for example, the relation of elementary equivalence. Two models 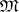 and
and 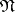 of
of 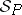 are elementarily equivalent if
are elementarily equivalent if 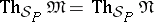 .
.
Let 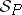 be a semantical system. Two models
be a semantical system. Two models 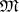 and
and 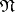 of
of 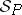 are elementarily equivalent if and only if there is an isomorphism
are elementarily equivalent if and only if there is an isomorphism 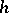 between the Leibniz-reduced meaning matrices that commutes with the meaning functions, i.e.,
between the Leibniz-reduced meaning matrices that commutes with the meaning functions, i.e.,
A) 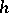 is an isomorphism between
is an isomorphism between 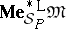 and
and 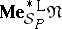 such that
such that 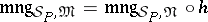 ; and
; and
B) 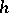 preserves the truth set, i.e.,
preserves the truth set, i.e., 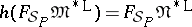 .
.
Two different classes of algebras are associated with each semantical system 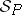 :
:
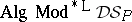 , the algebraic semantics of the underlying deductive system of
, the algebraic semantics of the underlying deductive system of 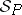 ; and
; and
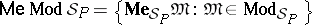 , the class of meaning algebras of
, the class of meaning algebras of 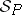 .
. 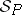 is protoalgebraic, equivalential, finitely equivalential, algebraizable, or finitely algebraizable if its underlying deductive system
is protoalgebraic, equivalential, finitely equivalential, algebraizable, or finitely algebraizable if its underlying deductive system 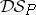 has the property and the meaning matrix of every model of
has the property and the meaning matrix of every model of  is Leibniz-reduced, i.e., if
is Leibniz-reduced, i.e., if 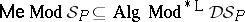 . In this case it can be shown that
. In this case it can be shown that 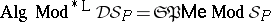 .
.
In general, for a deductive system 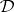 there are many different semantical systems with underlying deductive system
there are many different semantical systems with underlying deductive system 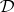 . A natural semantical system for classical propositional logic is obtained by considering only the interpretations of
. A natural semantical system for classical propositional logic is obtained by considering only the interpretations of 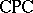 whose underlying algebra is a Boolean algebra of sets. More precisely, a model is a pair
whose underlying algebra is a Boolean algebra of sets. More precisely, a model is a pair 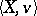 , where
, where 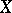 is a set and
is a set and  assigns a subset of
assigns a subset of 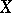 to each atomic formula in
to each atomic formula in 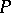 . The meaning function is the unique homomorphism from
. The meaning function is the unique homomorphism from  to the Boolean algebra of subsets of
to the Boolean algebra of subsets of 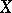 that extends
that extends  .
. 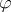 is valid in
is valid in 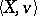 if its meaning is
if its meaning is 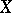 .
.
A semantical system for 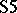 is obtained in a similar way. A model is a three-tuple
is obtained in a similar way. A model is a three-tuple 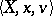 , where
, where 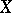 is a set,
is a set, 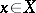 , and
, and  assigns subsets of
assigns subsets of 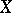 to atomic formulas. The meaning function is the unique homomorphism from
to atomic formulas. The meaning function is the unique homomorphism from  into the Boolean algebra of subsets of
into the Boolean algebra of subsets of 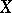 extending
extending  such that, for every formula
such that, for every formula 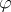 , the meaning of
, the meaning of 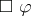 is
is 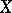 if the meaning of
if the meaning of 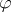 is
is  ; otherwise the meaning of
; otherwise the meaning of 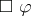 is the empty set.
is the empty set. 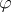 is valid in
is valid in 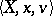 if
if  is contained in the meaning of
is contained in the meaning of 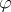 .
. 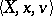 represents a so-called "possible worlds" model for
represents a so-called "possible worlds" model for 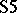 ;
; 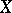 is the set of possible worlds and a formula is valid in the model if it is true at the distinguished "real world"
is the set of possible worlds and a formula is valid in the model if it is true at the distinguished "real world"  .
.
One of the standard semantical systems for the first-order predicate logic has as its models structures of the form 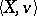 , where
, where 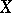 is a non-empty set and
is a non-empty set and  assigns a subset of
assigns a subset of 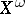 to each atomic formula. It is assumed that the individual variable symbols are arranged in an
to each atomic formula. It is assumed that the individual variable symbols are arranged in an 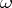 -sequence. The meaning function is the unique homomorphism from
-sequence. The meaning function is the unique homomorphism from 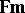 into the Boolean algebra of subsets of
into the Boolean algebra of subsets of 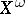 extending
extending  such that, for each formula
such that, for each formula 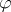 , the meaning of
, the meaning of 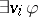 is the "cylinder" that is swept out by moving the meaning of
is the "cylinder" that is swept out by moving the meaning of 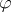 parallel to the
parallel to the 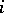 th coordinate. The meaning algebra is the subalgebra of the
th coordinate. The meaning algebra is the subalgebra of the 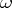 -dimensional cylindric set algebra over
-dimensional cylindric set algebra over 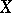 generated by the
generated by the 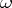 -ary relations that are the meanings of the atomic formulas. Elementary equivalence in first-order logic is essentially captured by the notion of elementary equivalence in the semantical systems of this kind. The characterization of elementary equivalence given by A) and B) provides a way of investigating elementary equivalence algebraically.
-ary relations that are the meanings of the atomic formulas. Elementary equivalence in first-order logic is essentially captured by the notion of elementary equivalence in the semantical systems of this kind. The characterization of elementary equivalence given by A) and B) provides a way of investigating elementary equivalence algebraically.
The algebraic study of some model-theoretic notions, such as definability, require semantical systems over varying sets of atomic formulas. A system 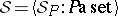 of semantical systems is called a general semantical system if the
of semantical systems is called a general semantical system if the 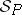 are compatible in the sense that, for all
are compatible in the sense that, for all 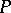 and
and 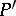 ,
, 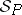 and
and 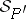 are isomorphic in the natural sense whenever
are isomorphic in the natural sense whenever 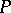 and
and 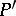 have the same cardinality, and, if
have the same cardinality, and, if 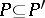 , then every model of
, then every model of 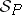 extends to a model of
extends to a model of 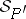 and every model of
and every model of 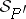 restricts to a model of
restricts to a model of 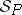 . A general semantical system
. A general semantical system 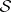 is protoalgebraic, equivalential, finitely equivalential, algebraizable, or finitely algebraizable if each of its component semantical systems
is protoalgebraic, equivalential, finitely equivalential, algebraizable, or finitely algebraizable if each of its component semantical systems 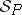 has this property.
has this property.
For every general semantical system 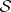 ,
, 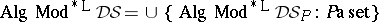 and
and 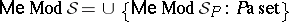 .
.
Let 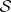 be a general semantical system. Let
be a general semantical system. Let 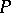 ,
, 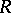 and
and 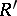 be disjoint sets of atomic formulas, and let
be disjoint sets of atomic formulas, and let  be a bijection between
be a bijection between 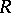 and
and 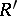 . Let
. Let 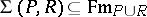 be a set of formulas whose atomic formulas are in
be a set of formulas whose atomic formulas are in 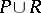 . Then:
. Then:
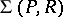 defines
defines 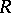 explicitly over
explicitly over 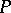 (in
(in 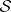 ) if for every
) if for every 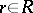 there exists a
there exists a 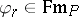 such that, for every
such that, for every 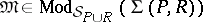 ,
,  .
.
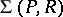 defines
defines 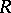 implicitly over
implicitly over 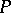 (in
(in 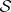 ) if for every
) if for every 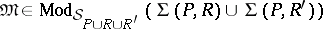 and every
and every 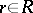 ,
,
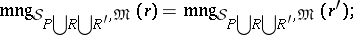 |
here  denotes the set of formulas obtained from
denotes the set of formulas obtained from 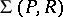 by replacing each
by replacing each 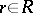 by
by 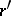 .
.
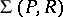 is a strong implicit definition of
is a strong implicit definition of 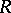 over
over 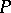 (in
(in 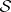 ) if it defines
) if it defines 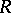 implicitly over
implicitly over 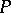 and every
and every  has an extension
has an extension  .
.
 has the (weak) Beth definability property if for all
has the (weak) Beth definability property if for all 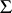 ,
, 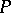 and
and 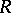 as above,
as above, 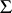 defines
defines 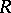 implicitly over
implicitly over 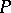 (in the strong sense), then
(in the strong sense), then 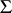 defines
defines 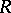 explicitly over
explicitly over 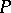 . Explicit definability always implies implicit definability. This is the well-known method of A. Padoa formulated in abstract algebraic logic.
. Explicit definability always implies implicit definability. This is the well-known method of A. Padoa formulated in abstract algebraic logic.
The algebraic analogue of the property of Beth is surjectivity of epimorphisms. Let  be a class of algebras over the same language type. A homomorphism
be a class of algebras over the same language type. A homomorphism 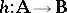 , where
, where  , is called an epimorphism over
, is called an epimorphism over  if for any pair of homomorphisms
if for any pair of homomorphisms 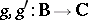 , if
, if 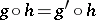 , then
, then 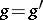 .
.
Let 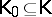 be classes of algebras over the same language type. A homomorphism
be classes of algebras over the same language type. A homomorphism 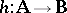 , where
, where 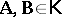 , is said to be
, is said to be  -extensible over
-extensible over  if for any
if for any 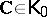 and every surjection
and every surjection 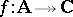 there is a
there is a 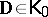 and
and 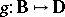 such that
such that 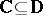 and
and 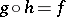 .
.
Let  be a finitely algebraizable generalized semantical system. Then:
be a finitely algebraizable generalized semantical system. Then:
I)  has the Beth definability property if and only if every epimorphism over
has the Beth definability property if and only if every epimorphism over 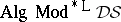 is surjective;
is surjective;
II)  has the weak Beth definability property if and only if every
has the weak Beth definability property if and only if every  )-extensible epimorphism of
)-extensible epimorphism of 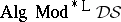 is surjective.
is surjective.
The algebraic characterization of the weak Beth property requires a semantics-based context, but the result on the ordinary Beth property can be reformulated within logistic abstract algebraic logic and extended to equivalence deductive systems.
The main references for semantics-based abstract algebraic logic are [a26], [a2], [a3]. For the results on definability, see [a23] and [a36].
References
| [a1] | A.R. Anderson, N.D. Belnap, "Entailment. The logic of relevance and necessity" , I , Princeton Univ. Press (1975) |
| [a2] | H. Andréka, A. Kurucz, I. Németi, I. Sain, "Applying algebraic logic: A general methodology" , Proc. Summer School of Algebraic Logic , Kluwer Acad. Publ. (to appear) (Short version in: [A26]) |
| [a3] | H. Andréka, I. Németi, "General algebraic logic: A perspective on ``what is logic" D. Gabbay (ed.) , What is a logical system? , Clarendon Press (1994) pp. 485–569 |
| [a4] | S.L. Bloom, R. Suszko, "Investigations into the sentential logic with identity" Notre Dame J. Formal Logic , 13 (1972) pp. 289–308 |
| [a5] | W.J. Blok, D. Pigozzi, "Abstract algebraic logic and the deduction theorem" Bull. Symbolic Logic (to appear) |
| [a6] | W.J. Blok, D. Pigozzi, "Algebraizable logics" , Memoirs , 396 , Amer. Math. Soc. (1989) |
| [a7] | W.J. Blok, D. Pigozzi, "Protoalgebraic logics" Studia Logica , 45 (1986) pp. 337–369 |
| [a8] | W.J. Blok, D. Pigozzi, "Algebraic semantics for universal Horn logic without equality" A. Romanowska (ed.) J.D.H. Smith (ed.) , Universal Algebra and Quasigroup Theory , Heldermann (1992) pp. 1–56 |
| [a9] | L.H. Chin, A. Tarski, "Distributive and modular laws in relation algebras" Univ. California Publ. Math. New Ser. , 1 : 9 (1951) pp. 341–384 |
| [a10] | J. Czelakowski, R. Jansana, "Weakly algebraizable logics" J. Symbolic Logic , 65 (2000) pp. 641–668 |
| [a11] | J. Czelakowski, "Algebraic aspects of deduction theorems" Studia Logica , 44 (1985) pp. 369–387 |
| [a12] | J. Czelakowski, "Protoalgebraic logics" , Trends in Logic—Studia Logica Libr. , 10 , Kluwer Acad. Publ. (2001) |
| [a13] | J. Czelakowski, "Equivalential logics I—II" Studia Logica , 40 (1981) pp. 227–236; 355–372 |
| [a14] | J. Czelakowski, "Consequence operations: Foundational studies" Techn. Rept. Inst. Philosophy and Sociology Polish Acad. Sci. (1992) |
| [a15] | P. Dellunde, R. Jansana, "Some characterization theorems for infinitary universal horn logic without equality" J. Symbolic Logic , 61 (1996) pp. 1242–1260 |
| [a16] | R. Elgueta, "Subdirect representation theory for classes without equality" Algebra Univ. , 40 (1998) pp. 201–246 |
| [a17] | R. Elgueta, "Characterizing classes defined without equality" Studia Logica , 58 (1997) pp. 357–394 |
| [a18] | J.M. Font, R. Jansana, "A general algebraic semantics for sentential logics" , Lecture Notes in Logic , 7 , Springer (1996) |
| [a19] | P.R. Halmos, "Algebraic logic I: Monadic Boolean algebras" Compositio Math. , 12 (1955) pp. 217–249 |
| [a20] | B. Herrmann, "Characterizing equivalential and algebraizable logics" Studia Logica , 58 (1997) pp. 305–323 |
| [a21] | B. Herrmann, "Equivalential and algebraizable logics" Studia Logica , 57 (1996) pp. 419–436 |
| [a22] | L. Henkin, J.D. Monk, A. Tarski, "Cylindric algebras, Parts I—II" , North-Holland (1971/85) |
| [a23] | E. Hoogland, "Algebraic characterization of various Beth definability properties" Studia Logica , 65 (2000) pp. 91–112 |
| [a24] | J. Łoś, "O matrycach logicznych" Ser. B. Travaux de la Soc. Sci. et des Lettres de Wrocław , 19 (1949) |
| [a25] | J. Malinowski, "The deduction theorem for quantum logic—some negative results" J. Symbolic Logic , 55 (1990) pp. 615–625 |
| [a26] | H. Andréka, I. Németi, I. Sain, "Applying algebraic logic to logic" M. Nivat (ed.) et al. (ed.) , Algebraic Methodology and Software Techn. (AMAST'93, Proc. 3rd Internat. Conf. Algebraic Methodology and Software Techn.), Workshops in Computing , Springer (1994) pp. 3–26 |
| [a27] | K. Pałasińska, "Deductive systems and finite axiomatizability properties" PhD Thesis Iowa State Univ. (1994) |
| [a28] | H. Rasiowa, "An algebraic approach to non-classical logics" , North-Holland (1974) |
| [a29] | J. Rebagliato, V. Verdú, "On the algebraization of some Gentzen systems" Fundam. Inform. , 18 (1993) pp. 319–338 (Special Issue on Algebraic Logic and its Applications) |
| [a30] | R. Suszko, "Abolition of the Fregean axiom" , Logic Colloquium (Boston 1972/3) , Lecture Notes in Mathematics , 453 , Springer (1975) pp. 169–236 |
| [a31] | T. Smiley, "The independence of connectives" J. Symbolic Logic , 27 (1962) pp. 426–436 |
| [a32] | S.J. Surma, "On the origin and subsequent applications of the concept of the Lindenbaum algebra" , Logic, Methodology and Philosophy of Science VI (Hannover 1979) , North-Holland (1982) pp. 719–734 |
| [a33] | A. Tarski, "Über einige fundamentale Begriffe der Metamathematik" C.R. Soc. Sci. Lettr. Varsovie Cl. III , 23 (1930) pp. 22–29 |
| [a34] | A. Tarski, "Grundzüge der Systemenkalküls. Erster Teil" Fundam. Math. , 25 (1935) pp. 503–526 |
| [a35] | R. Wójcicki, "Theory of logical calculi. Basic theory of consequence operations" , Synthese Library , 199 , Reidel (1988) |
| [a36] | E. Hoogland, "Definability and interpolation. Model-theoretic investigations" , ILLC Dissert. Ser. DS-2001-05 , Inst. Language, Logic and Computation, Amsterdam (2001) |
| [a37] | W.J. Blok, D. Pigozzi, "Local deduction theorems in algebraic logic" H. Andréka (ed.) J.D. Monk (ed.) I. Németi (ed.) , Algebraic Logic (Proc. Conf. Budapest 1988) , Colloq. Math. Soc. J. Bolyai , 54 , North-Holland (1991) pp. 75–109 |
| [a38] | J. Czelakowski, "Filter-distributive logics" Studia Logica , 43 (1984) pp. 353–377 |
Abstract algebraic logic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_algebraic_logic&oldid=19239