Difference between revisions of "Absorbing state"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(→References: Feller: internal link) |
||
| Line 44: | Line 44: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Feller, "An introduction to probability theory and its applications" , '''1''' , Wiley (1968) | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''1''', Wiley (1968)</TD></TR></table> |
Revision as of 05:15, 30 March 2012
of a Markov chain 
2020 Mathematics Subject Classification: Primary: 60J10 [MSN][ZBL]
A state 
such that
 |
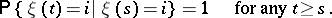An example of a Markov chain with absorbing state 
is a branching process.
The introduction of additional absorbing states is a convenient technique that enables one to examine the properties of trajectories of a Markov chain that are associated with hitting some set.
Example. Consider the set 
of states of a homogeneous Markov chain 
with discrete time and transition probabilities
 |
in which a subset 
is distinguished and suppose one has to find the probabilities
 |
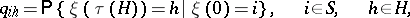where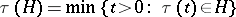 
is the moment of first hitting the set 
. If one introduces the auxiliary Markov chain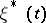 
differing from 
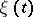only in that all states 
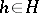are absorbing in 
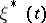, then for 
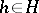the probabilities
 |
 |
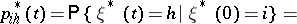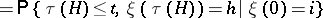are monotonically non-decreasing for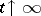 
and
 | (*) |
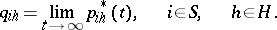By virtue of the basic definition of a Markov chain
 |
 |
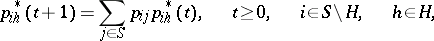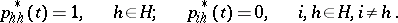The passage to the limit for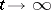 
taking into account (*) gives a system of linear equations for 
:
 |
 |
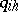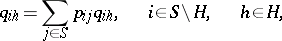References
| [1] | W. Feller, "An introduction to probability theory and its applications", 1, Wiley (1968) |
Absorbing state. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absorbing_state&oldid=23573