Absolutely continuous measures
Suppose that on the measurable space  there are given two measures
there are given two measures  and
and  (cf. also Measure). One says that
(cf. also Measure). One says that  is absolutely continuous with respect to
is absolutely continuous with respect to  (denoted
(denoted  ) if
) if  implies
implies  for any set
for any set  . One also says that
. One also says that 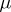 dominates
dominates  . If the measure
. If the measure  is finite (i.e.
is finite (i.e.  ), then
), then 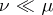 if and only if for any
if and only if for any  there exists a
there exists a  such that
such that  whenever
whenever 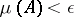 .
.
The Radon–Nikodým theorem says that if  and
and  are
are  -finite measures and
-finite measures and  , then there exists a
, then there exists a  -integrable non-negative function
-integrable non-negative function  (a density, cf. also Integrable function), called the Radon–Nikodým derivative, such that
(a density, cf. also Integrable function), called the Radon–Nikodým derivative, such that  . Two such densities
. Two such densities  and
and 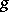 may differ only on a null set (see Measure), i.e.
may differ only on a null set (see Measure), i.e.  . An example of a density (with respect to the Lebesgue measure on the interval, i.e. the length) is the function
. An example of a density (with respect to the Lebesgue measure on the interval, i.e. the length) is the function 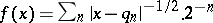 , where
, where 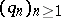 is the sequence of all rational numbers in this interval.
is the sequence of all rational numbers in this interval.
The measure is 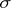 -finite if
-finite if 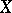 is the union of a countable family of sets with finite measure.
is the union of a countable family of sets with finite measure.
Given a reference measure 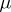 on
on 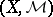 , any measure may be decomposed into a sum of
, any measure may be decomposed into a sum of  and
and  with
with 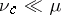 and
and 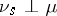 , i.e. an absolutely continuous and a singular part. This is called the Lebesgue decomposition.
, i.e. an absolutely continuous and a singular part. This is called the Lebesgue decomposition.
A set of non-zero measure that has no subsets of smaller, but still positive, measure is called an atom of the measure. It is a common mistake to claim that the singular part of a measure must be concentrated on points which are atoms. A singular measure may be atomless, as is shown by the measure concentrated on the standard Cantor set which puts zero on each gap of the set and  on the intersection of the set with the interval of generation
on the intersection of the set with the interval of generation  .
.
When some canonical measure  on
on  is fixed (as the Lebesgue measure on
is fixed (as the Lebesgue measure on 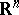 or its subsets or, more generally, the Haar measure on a topological group), one says that
or its subsets or, more generally, the Haar measure on a topological group), one says that  is absolutely continuous on
is absolutely continuous on  , meaning that
, meaning that  .
.
Two measures which are mutually absolutely continuous are called equivalent.
See also Absolute continuity.
References
| [a1] | H.L. Royden, "Real analysis" , Macmillan (1968) |
| [a2] | E. Hewitt, K. Stromberg, "Real and abstract analysis" , Springer (1965) |
Absolutely continuous measures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absolutely_continuous_measures&oldid=14254