Abelian difference set
Let 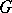 be a group of order
be a group of order  and
and 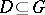 with
with 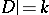 . Then
. Then 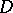 is called a
is called a 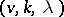 -difference set of order
-difference set of order 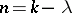 in
in  if every element
if every element  in
in 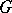 has exactly
has exactly 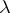 different representations
different representations 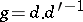 with
with 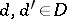 , see [a1]. For instance,
, see [a1]. For instance, 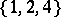 is a
is a 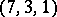 -difference set in the cyclic group of order
-difference set in the cyclic group of order 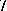 . If
. If 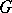 is Abelian (cyclic, non-Abelian), the difference set is called Abelian (cyclic, non-Abelian). Two difference sets
is Abelian (cyclic, non-Abelian), the difference set is called Abelian (cyclic, non-Abelian). Two difference sets 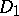 and
and 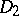 in
in 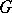 are equivalent if there is a group automorphism
are equivalent if there is a group automorphism 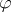 such that
such that  . The existence of a
. The existence of a 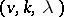 -difference set is equivalent to the existence of a symmetric
-difference set is equivalent to the existence of a symmetric  -design with
-design with 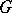 acting as a regular automorphism group (cf. also Difference set). If two difference sets correspond to isomorphic designs, the difference sets are called isomorphic. Given certain parameters
acting as a regular automorphism group (cf. also Difference set). If two difference sets correspond to isomorphic designs, the difference sets are called isomorphic. Given certain parameters  ,
, 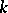 and
and 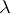 and a group
and a group 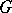 , the problem is to construct a difference set with those parameters or prove non-existence. To prove non-existence of Abelian difference sets, results from algebraic number theory are required: The existence of the difference set implies the existence of an algebraic integer of absolute value
, the problem is to construct a difference set with those parameters or prove non-existence. To prove non-existence of Abelian difference sets, results from algebraic number theory are required: The existence of the difference set implies the existence of an algebraic integer of absolute value  in some cyclotomic field. In several cases one can prove that no such element exists, see [a5]. Another approach for non-existence results uses multipliers: A multiplier of an Abelian difference set in
in some cyclotomic field. In several cases one can prove that no such element exists, see [a5]. Another approach for non-existence results uses multipliers: A multiplier of an Abelian difference set in 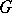 is an automorphism
is an automorphism 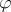 of
of 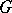 such that
such that 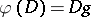 . A statement that certain group automorphisms have to be multipliers of putative difference sets is called a multiplier theorem. It is known, for instance, that the mapping
. A statement that certain group automorphisms have to be multipliers of putative difference sets is called a multiplier theorem. It is known, for instance, that the mapping 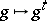 is a multiplier of an Abelian difference set provided that: i)
is a multiplier of an Abelian difference set provided that: i) 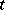 divides the order
divides the order  ; ii)
; ii) 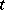 is relatively prime to
is relatively prime to  ; and iii)
; and iii) 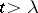 . Several generalizations of this theorem are known, see [a1].
. Several generalizations of this theorem are known, see [a1].
On the existence side, some families of Abelian difference sets are known, see [a3].
Examples.
The most popular examples are as follows.
Cyclic 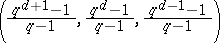 -difference sets,
-difference sets, 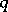 a prime power. The classical construction of these difference sets (elements in the multiplicative group of
a prime power. The classical construction of these difference sets (elements in the multiplicative group of 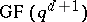 whose trace is
whose trace is  ) corresponds to the classical point-hyperplane designs of a finite projective space. For non-equivalent cyclic examples with the same parameters, see [a5].
) corresponds to the classical point-hyperplane designs of a finite projective space. For non-equivalent cyclic examples with the same parameters, see [a5].
Quadratic residues in 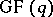 ,
, 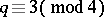 (Paley difference sets). Some other cyclotomic classes yield difference sets too, see [a1].
(Paley difference sets). Some other cyclotomic classes yield difference sets too, see [a1].
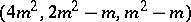 -difference sets,
-difference sets, 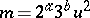 , where
, where  is a product of odd prime numbers (Hadamard difference sets, [a2]). If
is a product of odd prime numbers (Hadamard difference sets, [a2]). If 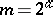 , it is known that an Abelian Hadamard difference set exists if and only if the exponent of
, it is known that an Abelian Hadamard difference set exists if and only if the exponent of 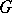 is at most
is at most 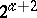 , see [a4].
, see [a4].
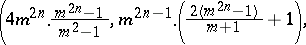
 -difference sets, where
-difference sets, where 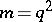 (
( an odd prime power) or
an odd prime power) or 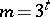 or
or 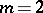 (generalized Hadamard difference sets, [a2]).
(generalized Hadamard difference sets, [a2]).
 -difference sets,
-difference sets, 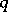 a prime power (McFarland difference sets).
a prime power (McFarland difference sets).
References
| [a1] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1986) |
| [a2] | Y.Q. Chen, "On the existence of abelian Hadamard difference sets and generalized Hadamard difference sets" Finite Fields and Appl. (to appear) |
| [a3] | D. Jungnickel, A. Pott, "Difference sets: Abelian" Ch.J. Colbourn (ed.) J.H. Dinitz (ed.) , CRC Handbook of Combinatorial Designs , CRC (1996) pp. 297–307 |
| [a4] | R.G. Kraemer, "Proof of a conjecture on Hadamard  -groups" J. Combinatorial Th. A , 63 (1993) pp. 1–10 -groups" J. Combinatorial Th. A , 63 (1993) pp. 1–10 |
| [a5] | A. Pott, "Finite geometry and character theory" , Lecture Notes in Mathematics , 1601 , Springer (1995) |
Abelian difference set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abelian_difference_set&oldid=39966