ANOVA
analysis of variance
Here, ANOVA will be understood in the wide sense, i.e., equated to the univariate linear model whose model equation is
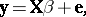 | (a1) |
in which 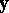 is an
is an 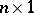 observable random vector,
observable random vector, 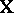 is a known
is a known 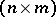 -matrix (the "design matrix" ),
-matrix (the "design matrix" ), 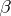 is an
is an 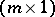 -vector of unknown parameters, and
-vector of unknown parameters, and  is an
is an 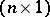 -vector of unobservable random variables
-vector of unobservable random variables 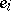 (the "errors" ) that are assumed to be independent and to have a normal distribution with mean
(the "errors" ) that are assumed to be independent and to have a normal distribution with mean  and unknown variance
and unknown variance 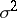 (i.e., the
(i.e., the 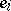 are independent identically distributed
are independent identically distributed 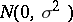 ). It is assumed throughout that
). It is assumed throughout that 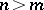 . Inference is desired on
. Inference is desired on 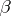 and
and 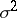 . The
. The 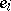 may represent measurement error and/or inherent variability in the experiment. The model equation (a1) can also be expressed in words by:
may represent measurement error and/or inherent variability in the experiment. The model equation (a1) can also be expressed in words by: 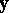 has independent normal elements
has independent normal elements 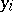 with common, unknown variance and expectation
with common, unknown variance and expectation 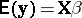 , in which
, in which 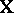 is known and
is known and 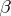 is unknown. In most experimental situations the assumptions made on
is unknown. In most experimental situations the assumptions made on  should be regarded as an approximation, though often a good one. Studies on some of the effects of deviations from these assumptions can be found in [a48], Chap. 10, and [a51] discusses diagnostics and remedies for lack of fit in linear regression models. To a certain extent the ANOVA ideas have been carried over to discrete data, then called the log-linear model; see [a6], and [a10].
should be regarded as an approximation, though often a good one. Studies on some of the effects of deviations from these assumptions can be found in [a48], Chap. 10, and [a51] discusses diagnostics and remedies for lack of fit in linear regression models. To a certain extent the ANOVA ideas have been carried over to discrete data, then called the log-linear model; see [a6], and [a10].
MANOVA (multivariate analysis of variance) is the multivariate generalization of ANOVA. Its model equation is obtained from (a1) by replacing the column vectors 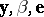 by matrices
by matrices 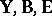 to obtain
to obtain
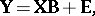 | (a2) |
where 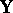 and
and 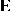 are
are 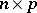 ,
, 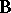 is
is 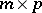 , and
, and 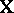 is as in (a1). The assumption on
is as in (a1). The assumption on 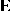 is that its
is that its  rows are independent identically distributed
rows are independent identically distributed 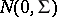 , i.e., the common distribution of the independent rows is
, i.e., the common distribution of the independent rows is 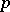 -variate normal with
-variate normal with  mean and
mean and 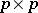 non-singular covariance matrix
non-singular covariance matrix 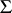 .
.
GMANOVA (generalized multivariate analysis of variance) generalizes the model equation (a2) of MANOVA to
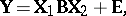 | (a3) |
in which 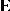 is as in (a2),
is as in (a2), 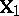 is as
is as 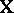 in (a2),
in (a2), 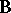 is
is 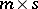 , and
, and 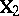 is an
is an 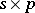 second design matrix.
second design matrix.
Logically, it would seem that it suffices to deal only with (a3), since (a2) is a special case of (a3), and (a1) of (a2). This turns out to be impossible and it is necessary to treat the three topics in their own right. This will be done, below. For unexplained terms in the fields of estimation and testing hypotheses, see [a30], [a31] (and also Statistical hypotheses, verification of; Statistical estimation).
ANOVA.
This field is very large, well-developed, and well-documented. Only a brief outline is given here; see the references for more detail. An excellent introduction to the essential elements of the field is [a48] and a short history is given in [a47], Sect. 2. Brief descriptions are also given in [a56], headings Anova; General Linear Model. Other references are [a49] [a50], [a43], [a26], and [a15]. A collection of survey articles on many aspects of ANOVA (and of MANOVA and GMANOVA) can be found in [a14].
In (a1) it is assumed that the parameter vector 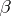 is fixed (even though unknown). This is called a fixed effects model, or Model I. In some experimental situations it is more appropriate to consider
is fixed (even though unknown). This is called a fixed effects model, or Model I. In some experimental situations it is more appropriate to consider 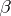 random and inference is then about parameters in the distribution of
random and inference is then about parameters in the distribution of 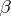 . This is called a random effects model, or Model II. It is called a mixed model if some elements of
. This is called a random effects model, or Model II. It is called a mixed model if some elements of 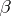 are fixed, others random. There are also various randomization models that are not described by (a1). For reasons of space limitation, only the fixed effects model will be treated here. For the other models see [a48], Chaps. 7, 8, 9.
are fixed, others random. There are also various randomization models that are not described by (a1). For reasons of space limitation, only the fixed effects model will be treated here. For the other models see [a48], Chaps. 7, 8, 9.
The name "analysis of variance" was coined by R.A. Fisher, who developed statistical techniques for dealing with agricultural experiments; see [a48], Sect. 1.1: references to Fisher. As a typical example, consider the two-way layout for the simultaneous study of two different factors, for convenience denoted by 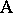 and
and 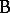 , on the measurement of a certain quantity. Let
, on the measurement of a certain quantity. Let 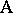 have levels
have levels 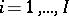 , and let
, and let 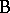 have levels
have levels 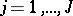 . For each
. For each 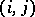 combination, measurements
combination, measurements 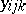 ,
, 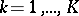 , are made. For instance, in a study of the effects of different varieties and different fertilizers on the yield of tomatoes, let
, are made. For instance, in a study of the effects of different varieties and different fertilizers on the yield of tomatoes, let 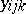 be the weight of ripe tomatoes from plant
be the weight of ripe tomatoes from plant 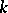 of variety
of variety 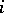 using fertilizer
using fertilizer 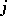 . The model equation is
. The model equation is
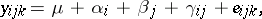 | (a4) |
and it is assumed that the 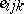 are independent identically distributed
are independent identically distributed 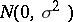 . This is of the form (a1) after the
. This is of the form (a1) after the 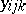 and
and 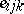 are strung out to form the column vectors
are strung out to form the column vectors 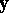 and
and  of (a1) with
of (a1) with  ; similarly, the parameters on the right-hand side of (a4) form an
; similarly, the parameters on the right-hand side of (a4) form an 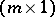 -vector
-vector 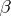 , with
, with 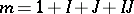 ; finally,
; finally, 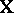 in (a1) has one column for each of the
in (a1) has one column for each of the 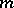 parameters, and in row
parameters, and in row 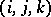 of
of 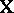 there is a
there is a 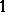 in the columns for
in the columns for 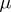 ,
, 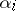 ,
, 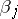 , and
, and 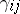 , and
, and  s elsewhere. Some of the customary terminology is as follows. Each
s elsewhere. Some of the customary terminology is as follows. Each 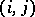 combination is a cell. In the example (a4), each cell has the same number
combination is a cell. In the example (a4), each cell has the same number 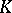 of observations (balanced design); in general, the cell numbers need not be equal. The parameters on the right-hand side of (a4) are called the effects:
of observations (balanced design); in general, the cell numbers need not be equal. The parameters on the right-hand side of (a4) are called the effects: 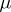 is the general mean, the
is the general mean, the 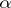 s are the main effects for factor
s are the main effects for factor 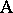 , the
, the 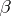 s for
s for 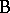 , and the
, and the 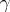 s are the interactions.
s are the interactions.
The extension to more than two factors is immediate. There are then potentially more types of interactions; e.g., in a three-way layout there are three types of two-factor interactions and one type of three-factor interactions. Layouts of this type are called factorial, and completely crossed if there is at least one observation in each cell. The latter may not always be feasible for practical reasons if the number of cells is large. In that case it may be necessary to restrict observations to only a fraction of the cells and assume certain interactions to be  . The judicious choice of this is the subject of design of experiments; see [a26], [a15].
. The judicious choice of this is the subject of design of experiments; see [a26], [a15].
A different type of experiment involves regression. In the simplest case the measurement 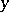 of a certain quantity may be modelled as
of a certain quantity may be modelled as 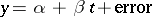 , where
, where 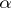 and
and 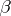 are unknown real-valued parameters and
are unknown real-valued parameters and 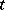 is the value of some continuously measurable quantity such as time, temperature, distance, etc.. This is called linear regression (i.e., linear in
is the value of some continuously measurable quantity such as time, temperature, distance, etc.. This is called linear regression (i.e., linear in 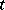 ). More generally, there could be an arbitrary polynomial in
). More generally, there could be an arbitrary polynomial in 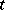 on the right-hand side. As an example, assume quadratic regression and suppose
on the right-hand side. As an example, assume quadratic regression and suppose 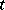 denotes time. Let
denotes time. Let 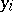 be the measurement on
be the measurement on 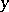 at time
at time 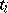 ,
, 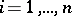 . The model equation is
. The model equation is 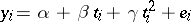 , which is of the form (a1) with
, which is of the form (a1) with 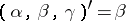 of (a1). The matrix
of (a1). The matrix 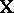 of (a1) has three columns corresponding to
of (a1) has three columns corresponding to 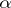 ,
, 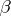 , and
, and 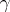 ; the
; the 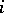 th row of
th row of 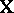 is
is 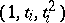 . Functions of
. Functions of  other than polynomials are sometimes appropriate. Frequently,
other than polynomials are sometimes appropriate. Frequently, 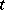 is referred to as a regressor variable or independent variable, and
is referred to as a regressor variable or independent variable, and 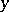 the dependent variable. Instead of one regressor variable there may be several (multiple regression).
the dependent variable. Instead of one regressor variable there may be several (multiple regression).
Factors such as 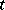 above whose values can be measured on a continuous scale are called quantitative. In contrast, categorical variables (e.g., variety of tomato) are called qualitative. A quantitative factor
above whose values can be measured on a continuous scale are called quantitative. In contrast, categorical variables (e.g., variety of tomato) are called qualitative. A quantitative factor 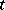 may be treated qualitatively if the experiment is conducted at several values, say
may be treated qualitatively if the experiment is conducted at several values, say 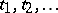 , but these are only regarded as levels
, but these are only regarded as levels 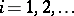 of the factor whereas the actual values
of the factor whereas the actual values 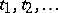 are ignored. The name analysis of variance is often reserved for models that have only factors that are qualitative or treated qualitatively. In contrast, regression analysis has only quantitative factors. Analysis of covariance covers models that have both kinds of factors. See [a48], Chap. 6, for more detail.
are ignored. The name analysis of variance is often reserved for models that have only factors that are qualitative or treated qualitatively. In contrast, regression analysis has only quantitative factors. Analysis of covariance covers models that have both kinds of factors. See [a48], Chap. 6, for more detail.
Another important distinction involving factors is between the notions of crossing and nesting. Two factors 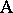 and
and 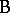 are crossed if each level of
are crossed if each level of 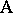 can occur with each level of
can occur with each level of 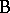 (completely crossed if there is at least one observation for each combination of levels, otherwise incompletely or partly crossed). For instance, in the tomato example of the two-way layout (a4), the two factors are crossed since each variety
(completely crossed if there is at least one observation for each combination of levels, otherwise incompletely or partly crossed). For instance, in the tomato example of the two-way layout (a4), the two factors are crossed since each variety 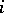 can be grown with any fertilizer
can be grown with any fertilizer 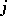 . In contrast, factor
. In contrast, factor 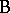 is said to be nested within factor
is said to be nested within factor 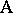 if every level of
if every level of 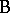 can only occur with one level of
can only occur with one level of 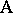 . For instance, suppose two different manufacturing processes (factor
. For instance, suppose two different manufacturing processes (factor 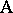 ) for the production of cords have to be compared. From each of the two processes several cords are chosen (factor
) for the production of cords have to be compared. From each of the two processes several cords are chosen (factor 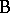 ), each cord cut into several pieces and the breaking strength of each piece measured. Here each cord goes only with one of the processes so that
), each cord cut into several pieces and the breaking strength of each piece measured. Here each cord goes only with one of the processes so that 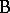 is nested within
is nested within 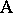 . Nested factors should be treated more realistically as random. However, for the analysis it is necessary to analyze the corresponding fixed effects model first. See [a48], Sect. 5.3, for more examples and detail.
. Nested factors should be treated more realistically as random. However, for the analysis it is necessary to analyze the corresponding fixed effects model first. See [a48], Sect. 5.3, for more examples and detail.
Estimation and testing hypotheses.
The main interest is in inference on linear functions of the parameter vector 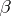 of (a1), called parametric functions, i.e., functions of the form
of (a1), called parametric functions, i.e., functions of the form 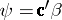 , with
, with  of order
of order 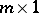 . Usually one requires point estimators (cf. also Point estimator) of such
. Usually one requires point estimators (cf. also Point estimator) of such 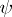 s to be unbiased (cf. also Unbiased estimator). Of particular interest are the elements of the vector
s to be unbiased (cf. also Unbiased estimator). Of particular interest are the elements of the vector 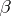 . However, there is a complication arising from the fact that the design matrix
. However, there is a complication arising from the fact that the design matrix 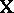 in (a1) may be of less than maximal rank (the columns can be linearly dependent). This happens typically in analysis of variance models (but not usually in regression models). For instance, in the two-way layout (a4) the sum of the columns for the
in (a1) may be of less than maximal rank (the columns can be linearly dependent). This happens typically in analysis of variance models (but not usually in regression models). For instance, in the two-way layout (a4) the sum of the columns for the 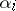 equals the column for
equals the column for 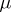 . If
. If 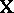 is of less than full rank, then the elements of
is of less than full rank, then the elements of 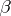 are not identifiable in the sense that even if the error vector
are not identifiable in the sense that even if the error vector  in (a1) were
in (a1) were  , so that
, so that 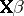 is known, there is no unique solution for
is known, there is no unique solution for 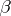 . A fortiori the elements of
. A fortiori the elements of 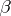 do not possess unbiased estimators. Yet, there are parametric functions that do have an unbiased estimator; they are called estimable. It is easily shown that
do not possess unbiased estimators. Yet, there are parametric functions that do have an unbiased estimator; they are called estimable. It is easily shown that 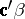 is estimable if and only if
is estimable if and only if 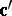 is in the row space of
is in the row space of 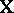 (see [a48], Sect. 1.4). In particular, if one sets
(see [a48], Sect. 1.4). In particular, if one sets 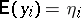 and takes
and takes 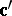 to be the
to be the 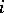 th row of
th row of 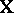 , then
, then 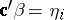 is estimable. Thus,
is estimable. Thus, 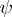 is estimable if and only if it is a linear combination of the elements of
is estimable if and only if it is a linear combination of the elements of 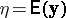 .
.
The complication presented by a design matrix 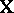 that is not of full rank may be handled in several ways. First, a re-parametrization with fewer parameters and fewer columns of
that is not of full rank may be handled in several ways. First, a re-parametrization with fewer parameters and fewer columns of 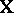 is possible. Second, a popular way is to impose side conditions on the parameters that make them unique. For instance, in the two-way layout (a4) often-used side conditions are:
is possible. Second, a popular way is to impose side conditions on the parameters that make them unique. For instance, in the two-way layout (a4) often-used side conditions are: 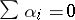 , or, equivalently,
, or, equivalently, 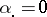 (where dotting on a subscript means averaging over that subscript); similarly,
(where dotting on a subscript means averaging over that subscript); similarly, 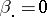 , and
, and 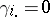 for all
for all 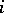 ,
, 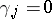 for all
for all 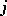 . Then all parameters are estimable and (for instance) the hypothesis
. Then all parameters are estimable and (for instance) the hypothesis 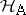 that all main effects of factor
that all main effects of factor 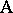 are
are  can be expressed by: All
can be expressed by: All 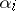 are equal to zero. A third way of dealing with an
are equal to zero. A third way of dealing with an 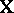 of less than full rank is to express all questions of inference in terms of estimable parametric functions. For instance, if in (a4) one writes
of less than full rank is to express all questions of inference in terms of estimable parametric functions. For instance, if in (a4) one writes 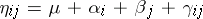 (
(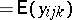 ), then all
), then all 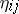 are estimable and
are estimable and 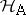 can be expressed by stating that all
can be expressed by stating that all 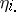 are equal, or, equivalently, that all
are equal, or, equivalently, that all 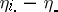 are equal to zero.
are equal to zero.
Another type of estimator that always exists is a least-squares estimator (LSE; cf. also Least squares, method of). A least-squares estimator of 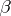 is any vector
is any vector 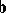 minimizing
minimizing 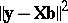 . A minimizing
. A minimizing 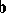 (unique if and only if
(unique if and only if 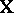 is of full rank) is denoted by
is of full rank) is denoted by 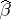 and satisfies the normal equations
and satisfies the normal equations
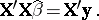 | (a5) |
If 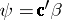 is estimable, then
is estimable, then 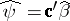 is unique (even when
is unique (even when 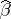 is not) and is called the least-squares estimator of
is not) and is called the least-squares estimator of 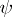 . By the Gauss–Markov theorem (cf. also Least squares, method of),
. By the Gauss–Markov theorem (cf. also Least squares, method of), 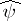 is the minimum variance unbiased estimator of
is the minimum variance unbiased estimator of 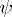 . See [a48], Sect. 1.4.
. See [a48], Sect. 1.4.
A linear hypothesis 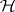 consists of one or more linear restrictions on
consists of one or more linear restrictions on 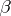 :
:
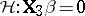 | (a6) |
with 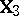 of order
of order 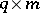 and rank
and rank 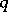 . Then
. Then 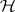 is to be tested against the alternative
is to be tested against the alternative 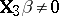 . Let
. Let 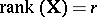 . The model (a1) together with
. The model (a1) together with 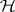 of (a6) can be expressed in geometric language as follows: The mean vector
of (a6) can be expressed in geometric language as follows: The mean vector 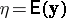 lies in a linear subspace
lies in a linear subspace  of
of  -dimensional space, spanned by the columns of
-dimensional space, spanned by the columns of 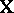 , and
, and 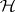 restricts
restricts 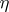 to a further subspace
to a further subspace 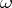 of
of  , where
, where 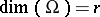 and
and 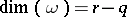 . Further analysis is simplified by a transformation to the canonical system, below.
. Further analysis is simplified by a transformation to the canonical system, below.
Canonical form.
There is a transformation 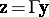 , with
, with 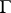 of order
of order 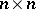 and orthogonal, so that the model (a1) together with the hypothesis (a6) can be put in the following form (in which
and orthogonal, so that the model (a1) together with the hypothesis (a6) can be put in the following form (in which  are the elements of
are the elements of  and
and 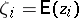 ):
):  are independent, normal, with common variance
are independent, normal, with common variance 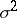 ;
; 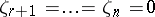 , and, additionally,
, and, additionally, 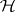 specifies
specifies 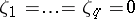 . Note that
. Note that 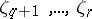 are unrestricted throughout. Any estimable parametric function can be expressed in the form
are unrestricted throughout. Any estimable parametric function can be expressed in the form 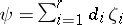 , with constants
, with constants  , and the least-squares estimator of
, and the least-squares estimator of 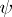 is
is 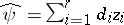 . To estimate
. To estimate 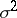 one forms the sum of squares for error
one forms the sum of squares for error 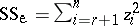 , and divides by
, and divides by 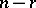 (
( degrees of freedom for the error) to form the mean square
degrees of freedom for the error) to form the mean square 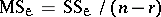 . Then
. Then 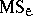 is an unbiased estimator of
is an unbiased estimator of 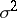 . A test of the hypothesis
. A test of the hypothesis 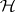 can be obtained by forming
can be obtained by forming 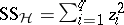 , with degrees of freedom
, with degrees of freedom 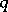 , and
, and 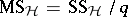 . Then, if
. Then, if 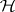 is true, the test statistic
is true, the test statistic 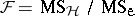 has an
has an 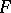 -distribution with degrees of freedom
-distribution with degrees of freedom 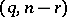 . For a test of
. For a test of 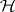 of level of significance
of level of significance 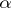 one rejects
one rejects 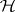 if
if 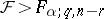 (
( the upper
the upper 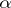 -point of the
-point of the 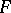 -distribution with degrees of freedom
-distribution with degrees of freedom 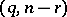 ). This is "the"
). This is "the" 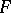 -test; it can be derived as a likelihood-ratio test (LR test) or as a uniformly most powerful invariant test (UMP invariant test) and has several other optimum properties; see [a48], Sect. 2.10. For the power of the
-test; it can be derived as a likelihood-ratio test (LR test) or as a uniformly most powerful invariant test (UMP invariant test) and has several other optimum properties; see [a48], Sect. 2.10. For the power of the 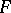 -test, see [a48], Sect. 2.8.
-test, see [a48], Sect. 2.8.
Simultaneous confidence intervals.
Let 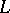 be the linear space of all parametric functions of the form
be the linear space of all parametric functions of the form 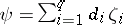 , i.e., all
, i.e., all 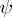 that are
that are  if
if 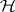 is true. The
is true. The 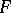 -test provides a way to obtain simultaneous confidence intervals for all
-test provides a way to obtain simultaneous confidence intervals for all 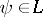 with confidence level
with confidence level 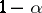 (cf. also Confidence interval). This is useful, for instance, in cases where
(cf. also Confidence interval). This is useful, for instance, in cases where 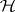 is rejected. Then any
is rejected. Then any 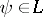 whose confidence interval does not include
whose confidence interval does not include  is said to be "significantly different from 0" and can be held responsible for the rejection of
is said to be "significantly different from 0" and can be held responsible for the rejection of 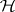 . Observe that
. Observe that 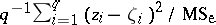 has an
has an 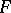 -distribution with degrees of freedom
-distribution with degrees of freedom 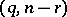 (whether or not
(whether or not 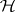 is true) so that this quantity is
is true) so that this quantity is 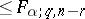 with probability
with probability 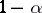 . This inequality can be converted into a family of double inequalities and leads to the simultaneous confidence intervals
. This inequality can be converted into a family of double inequalities and leads to the simultaneous confidence intervals
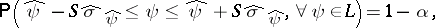 | (a7) |
in which 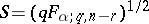 and
and 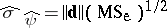 is the square root of the unbiased estimator of the variance
is the square root of the unbiased estimator of the variance 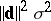 of
of 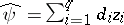 . Thus, the confidence interval for
. Thus, the confidence interval for 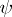 has endpoints
has endpoints 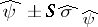 , and all
, and all 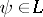 are covered by their confidence intervals simultaneously with probability
are covered by their confidence intervals simultaneously with probability 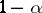 . Note that (a7) is stated without needing the canonical system so that the confidence intervals can be evaluated directly in the original system.
. Note that (a7) is stated without needing the canonical system so that the confidence intervals can be evaluated directly in the original system.
With help of (a7) the 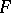 -test can also be expressed as follows:
-test can also be expressed as follows: 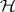 is accepted if and only if all confidence intervals with endpoints
is accepted if and only if all confidence intervals with endpoints 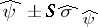 cover the value
cover the value  . More generally, it is convenient to make the following definition: a test of a hypothesis
. More generally, it is convenient to make the following definition: a test of a hypothesis 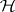 is exact with respect to a family of simultaneous confidence intervals for a family of parametric functions if
is exact with respect to a family of simultaneous confidence intervals for a family of parametric functions if 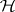 is accepted if and only if the confidence interval of every
is accepted if and only if the confidence interval of every 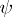 in the family includes the value of
in the family includes the value of 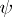 specified by
specified by 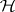 ; see [a52], [a53]. Thus, the
; see [a52], [a53]. Thus, the 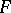 -test is exact with respect to the simultaneous confidence intervals (a7).
-test is exact with respect to the simultaneous confidence intervals (a7).
The confidence intervals obtained in (a7) are called Scheffé-type simultaneous confidence intervals. Shorter confidence intervals of Tukey-type within a smaller class of parametric functions are possible in some designs. This is applicable, for instance, in the two-way layout of (a4) with equal cell numbers if only differences between the  are considered important rather than all parametric functions that are
are considered important rather than all parametric functions that are  under
under 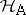 (so-called contrasts). See [a48], Sect. 3.6.
(so-called contrasts). See [a48], Sect. 3.6.
The canonical system is very useful to derive formulas and prove properties in a unified way, but it is usually not advisable in any given linear model to carry out the transformation 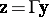 explicitly. Instead, the necessary expressions can be derived in the original system. For instance, if
explicitly. Instead, the necessary expressions can be derived in the original system. For instance, if 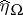 and
and 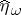 are the orthogonal projections of
are the orthogonal projections of 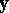 on
on  and on
and on 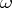 , respectively, then
, respectively, then 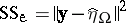 and
and 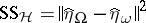 . These projections can be found by solving the normal equations (a5) (and one gets, for instance,
. These projections can be found by solving the normal equations (a5) (and one gets, for instance, 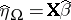 ), or by minimizing quadratic forms. As an example of the latter: In the two-way layout (a4), minimize
), or by minimizing quadratic forms. As an example of the latter: In the two-way layout (a4), minimize 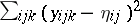 over the
over the 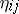 . This yields
. This yields 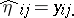 , so that
, so that 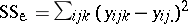 . If desired, formulas can be expressed in vector and matrix form. As an example, if
. If desired, formulas can be expressed in vector and matrix form. As an example, if 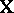 is of maximal rank, then (a5) yields
is of maximal rank, then (a5) yields 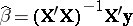 and
and 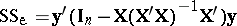 . Similar expressions hold under
. Similar expressions hold under 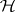 after replacing
after replacing 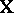 by a matrix whose columns span
by a matrix whose columns span 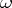 . If
. If 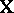 is not of maximal rank, then a generalized inverse may be employed. See [a43], Sect. 4a.3, and [a45].
is not of maximal rank, then a generalized inverse may be employed. See [a43], Sect. 4a.3, and [a45].
MANOVA.
There are several good textbooks on multivariate analysis that treat various aspects of MANOVA. Among the major ones are [a1], [a8], [a19], [a29], [a36], [a41], and [a43], Chap. 8. See also [a56], headings Multivariate Analysis; Multivariate Analysis Of Variance, and [a14]. The ideas involved in MANOVA are essentially the same as in ANOVA, but there is an added dimension in that the observations are now multivariate. For instance, if measurements are made on 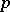 different features of the same individual, then this should be regarded as one observation on a
different features of the same individual, then this should be regarded as one observation on a 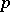 -variate distribution. The MANOVA model is given by (a2). A linear hypothesis on
-variate distribution. The MANOVA model is given by (a2). A linear hypothesis on 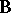 analogous to (a6) is
analogous to (a6) is
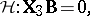 | (a8) |
with 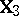 as in (a6). Any ANOVA testing problem defined by the choice of
as in (a6). Any ANOVA testing problem defined by the choice of 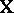 in (a1) and
in (a1) and 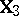 in (a6) carries over to the same kind of problem given by (a2) and (a8). However, since
in (a6) carries over to the same kind of problem given by (a2) and (a8). However, since 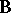 is a matrix, there are other ways than (a8) of formulating a linear hypothesis. The most obvious extension of (a8) is
is a matrix, there are other ways than (a8) of formulating a linear hypothesis. The most obvious extension of (a8) is
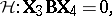 | (a9) |
in which 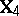 is a known
is a known 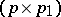 -matrix of rank
-matrix of rank 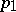 . However, (a9) can be reduced to (a8) by making the transformation
. However, (a9) can be reduced to (a8) by making the transformation 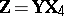 , of order
, of order 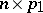 ,
, 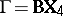 ,
, 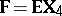 ; then the model is
; then the model is 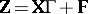 , with the rows of
, with the rows of 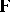 independent identically distributed
independent identically distributed 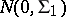 ,
, 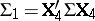 , and
, and 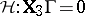 . Thus, the transformed problem is as (a2), (a8), with
. Thus, the transformed problem is as (a2), (a8), with 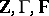 replacing
replacing 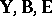 . This can be applied, for instance, to profile analysis; see [a29], Sect. 5.4 (A5), [a36], Sects. 4.6, 5.6.
. This can be applied, for instance, to profile analysis; see [a29], Sect. 5.4 (A5), [a36], Sects. 4.6, 5.6.
There is a canonical form of the MANOVA testing problem (a2), (a8) analogous to the ANOVA problem (a1), (a6), the difference being that the real-valued random variables 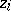 of ANOVA are replaced by
of ANOVA are replaced by 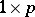 random vectors. These vectors form the rows of three random matrices,
random vectors. These vectors form the rows of three random matrices, 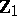 of order
of order 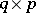 ,
, 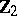 of order
of order 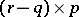 , and
, and 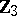 of order
of order 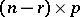 , all of whose rows are assumed independent and
, all of whose rows are assumed independent and 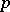 -variate normal with common non-singular covariance matrix
-variate normal with common non-singular covariance matrix 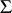 ; furthermore,
; furthermore, 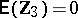 ,
, 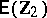 is unspecified, and
is unspecified, and 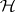 specifies
specifies 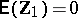 . It is assumed that
. It is assumed that 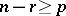 . Put
. Put 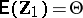 , so that
, so that 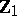 is an unbiased estimator of
is an unbiased estimator of 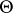 . For testing
. For testing 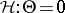 ,
, 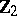 is ignored and the sums of squares
is ignored and the sums of squares 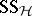 and
and 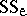 of ANOVA are replaced by the
of ANOVA are replaced by the 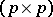 -matrices
-matrices 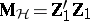 and
and 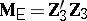 , respectively. An application of sufficiency plus the principle of invariance restricts tests of
, respectively. An application of sufficiency plus the principle of invariance restricts tests of 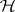 to those that depend only on the positive characteristic roots of
to those that depend only on the positive characteristic roots of 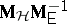 (
( the positive characteristic roots of
the positive characteristic roots of 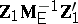 ). The case
). The case 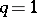 , when
, when 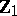 is a row vector, deserves special attention. It arises, for instance, when testing for zero mean in a single multivariate population or testing the equality of means in two such populations. Then
is a row vector, deserves special attention. It arises, for instance, when testing for zero mean in a single multivariate population or testing the equality of means in two such populations. Then 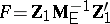 is the only positive characteristic root;
is the only positive characteristic root; 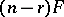 is called Hotelling's
is called Hotelling's 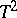 , and
, and 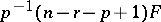 has an
has an 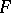 -distribution with degrees of freedom
-distribution with degrees of freedom 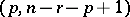 , central or non-central according as
, central or non-central according as 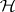 is true or false. Rejecting
is true or false. Rejecting 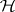 for large values of
for large values of 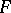 is uniformly most powerful invariant. If
is uniformly most powerful invariant. If 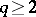 there is no best way of combining the
there is no best way of combining the 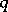 characteristic roots, so that there is no uniformly most powerful invariant test (unlike there is in ANOVA). The following tests have been proposed:
characteristic roots, so that there is no uniformly most powerful invariant test (unlike there is in ANOVA). The following tests have been proposed:
reject 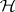 if
if 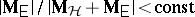 (Wilks LR test);
(Wilks LR test);
reject 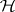 if the largest characteristic root of
if the largest characteristic root of 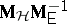 exceeds a constant (Roy's test);
exceeds a constant (Roy's test);
reject 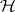 if
if 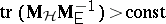 (Lawley–Hotelling test);
(Lawley–Hotelling test);
reject 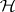 if
if 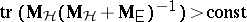 (Bartlett–Nanda–Pillai test). For references, see [a1], Sects. 8.3, 8.6, or [a36], Chap. 5. For distribution theory, see [a1], Sects. 8.4, 8.6, [a41], Sects. 10.4–10.6, [a55], Sect. 10.3. Tables and charts can be found in [a1], Appendix, and [a36], Appendix.
(Bartlett–Nanda–Pillai test). For references, see [a1], Sects. 8.3, 8.6, or [a36], Chap. 5. For distribution theory, see [a1], Sects. 8.4, 8.6, [a41], Sects. 10.4–10.6, [a55], Sect. 10.3. Tables and charts can be found in [a1], Appendix, and [a36], Appendix.
The problem of expressing the matrices 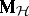 and
and 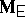 in terms of the original model given by (a2), (a8) is very similar to the situation in ANOVA. One way is to express
in terms of the original model given by (a2), (a8) is very similar to the situation in ANOVA. One way is to express 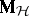 and
and 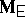 explicitly in terms of
explicitly in terms of 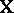 and
and 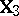 . Another is to consider the ANOVA problem with the same
. Another is to consider the ANOVA problem with the same 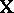 and
and 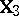 ; if explicit formulas exist for
; if explicit formulas exist for 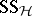 and
and 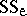 , they can be converted to
, they can be converted to 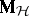 and
and 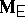 . For instance,
. For instance, 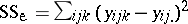 in the ANOVA two-way layout (a4) converts to
in the ANOVA two-way layout (a4) converts to 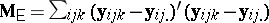 in the corresponding MANOVA problem, where now the
in the corresponding MANOVA problem, where now the 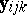 are
are 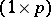 -vectors.
-vectors.
Point estimation.
In the canonical system 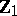 is an unbiased estimator and the maximum-likelihood estimator of
is an unbiased estimator and the maximum-likelihood estimator of  (cf. also Maximum-likelihood method). If
(cf. also Maximum-likelihood method). If 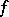 is a linear function of
is a linear function of 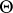 , then
, then 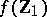 is both an unbiased estimator and a maximum-likelihood estimator of
is both an unbiased estimator and a maximum-likelihood estimator of 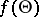 . An unbiased estimator of
. An unbiased estimator of 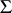 is
is 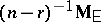 , whereas its maximum-likelihood estimator is
, whereas its maximum-likelihood estimator is 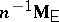 .
.
Confidence intervals and sets.
There are several kinds of linear functions of 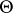 that are of interest. The direct analogue of a linear function of
that are of interest. The direct analogue of a linear function of 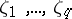 in ANOVA is a function of the form
in ANOVA is a function of the form 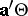 (with
(with  of order
of order 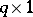 ), which is a
), which is a 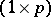 -vector. This leads to a confidence set in
-vector. This leads to a confidence set in 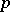 -space for
-space for 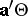 , rather than an interval. Simultaneous confidence sets for all
, rather than an interval. Simultaneous confidence sets for all 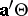 can be derived from any of the proposed tests for
can be derived from any of the proposed tests for 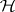 , but it turns out that only Roy's maximum root test is exact with respect to these confidence sets (and not, for instance, the LR test of Wilks); see [a52], [a53]. The same is true for simultaneous confidence sets for all
, but it turns out that only Roy's maximum root test is exact with respect to these confidence sets (and not, for instance, the LR test of Wilks); see [a52], [a53]. The same is true for simultaneous confidence sets for all 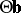 , and confidence intervals for all
, and confidence intervals for all 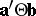 . Simultaneous confidence sets for all
. Simultaneous confidence sets for all 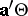 were given in [a18]. In [a46] simultaneous confidence intervals for all
were given in [a18]. In [a46] simultaneous confidence intervals for all 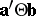 are derived (called "double linear compounds" ). These are special cases of all (possibly matrix-valued) functions of the form
are derived (called "double linear compounds" ). These are special cases of all (possibly matrix-valued) functions of the form 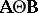 are treated in [a11]. The most general linear functions of
are treated in [a11]. The most general linear functions of 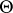 are of the form
are of the form 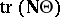 . Simultaneous confidence intervals for all such functions as
. Simultaneous confidence intervals for all such functions as 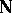 runs through all
runs through all 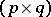 -matrices are given in [a37]. These are derived from a test defined in terms of a symmetric gauge function rather than from Roy's maximum root test. In [a52], [a53] a generalization of this is given if
-matrices are given in [a37]. These are derived from a test defined in terms of a symmetric gauge function rather than from Roy's maximum root test. In [a52], [a53] a generalization of this is given if 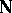 has its rank restricted; for
has its rank restricted; for 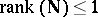 this reproduces the confidence intervals of [a46].
this reproduces the confidence intervals of [a46].
Step-down procedures.
Partition 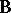 into its columns
into its columns 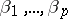 ; then
; then 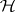 of (a8) is the intersection of the component hypotheses
of (a8) is the intersection of the component hypotheses 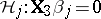 . Also partition
. Also partition 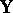 into its columns
into its columns 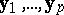 . Then for each
. Then for each 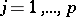 , the hypothesis
, the hypothesis 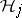 is tested with a univariate ANOVA
is tested with a univariate ANOVA 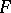 -test that depends only on
-test that depends only on 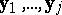 . If any
. If any 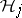 is rejected, then
is rejected, then 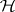 is rejected. The tests are independent, which permits easy determination of the overall level of significance in terms of the individual ones. For details, history of the subject and references, see [a38] and [a39], Sect. 3. A variation, based on
is rejected. The tests are independent, which permits easy determination of the overall level of significance in terms of the individual ones. For details, history of the subject and references, see [a38] and [a39], Sect. 3. A variation, based on 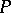 -values, is presented in [a40]. Step-down procedures are convenient, but it is shown in [a34] that even in the simplest case when
-values, is presented in [a40]. Step-down procedures are convenient, but it is shown in [a34] that even in the simplest case when 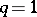 , a step-down test is not admissible. Furthermore, a step-down test is not exact with respect to simultaneous confidence intervals or confidence sets derived from the test for various linear functions of
, a step-down test is not admissible. Furthermore, a step-down test is not exact with respect to simultaneous confidence intervals or confidence sets derived from the test for various linear functions of 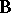 ; see [a53], Sect. 4.4. A generalization of step-down procedures is proposed in [a38] by grouping the column vectors of
; see [a53], Sect. 4.4. A generalization of step-down procedures is proposed in [a38] by grouping the column vectors of 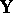 and
and 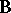 into blocks.
into blocks.
Random effects models.
Some references on this topic in MANOVA are [a2] and [a35]; see also references quoted therein.
Missing data.
Statistical experiments involving multivariate observations bring in an element that is not present with univariate observations, such as in ANOVA. Above, it has been taken for granted that of every individual in a sample all 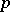 variates are observed. In practice this is not always true, for various reasons, in which case some of the observations have missing data. (This is not to be confused with the notion of empty cells in ANOVA.) If that happens, one can group all observations with complete data together as the complete sample and call the remaining observations an incomplete sample. From a slightly different point of view, the incomplete sample is sometimes considered extra data on some of the variates. The analysis of MANOVA problems is more complicated when there are missing data. In the simplest case, all missing data are on the same variates. This is a special case of nested missing data patterns. In the latter case explicit expressions of maximum-likelihood estimators are possible; see [a3] and the references therein. For more complicated missing data patterns explicit maximum-likelihood estimators are usually not available unless certain assumptions are made on the structure of the unknown covariance matrix
variates are observed. In practice this is not always true, for various reasons, in which case some of the observations have missing data. (This is not to be confused with the notion of empty cells in ANOVA.) If that happens, one can group all observations with complete data together as the complete sample and call the remaining observations an incomplete sample. From a slightly different point of view, the incomplete sample is sometimes considered extra data on some of the variates. The analysis of MANOVA problems is more complicated when there are missing data. In the simplest case, all missing data are on the same variates. This is a special case of nested missing data patterns. In the latter case explicit expressions of maximum-likelihood estimators are possible; see [a3] and the references therein. For more complicated missing data patterns explicit maximum-likelihood estimators are usually not available unless certain assumptions are made on the structure of the unknown covariance matrix 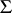 ; see [a3], [a4] and [a5]. The situation is even worse for testing. For instance, even in the simplest case of testing the hypothesis that the mean of a multivariate population is
; see [a3], [a4] and [a5]. The situation is even worse for testing. For instance, even in the simplest case of testing the hypothesis that the mean of a multivariate population is  , if in addition to a complete sample there is an incomplete one taken on a subset of the variates, then there is no locally (let alone uniformly) most-powerful test; see [a9]. Several aspects of estimation and testing in the presence of various patterns of missing data can be found in [a25], wherein also appear many references to other papers in the field.
, if in addition to a complete sample there is an incomplete one taken on a subset of the variates, then there is no locally (let alone uniformly) most-powerful test; see [a9]. Several aspects of estimation and testing in the presence of various patterns of missing data can be found in [a25], wherein also appear many references to other papers in the field.
GMANOVA.
This topic has not been recognized as a distinct entity within multivariate analysis until relatively recently. Consequently, most of today's (2000) knowledge of the subject is found in the research literature, rather than in textbooks. (There is an introduction to GMANOVA in [a41], Problem 10.18, and a little can be found in [a8], Sect. 9.6, second part.) A good exposition of testing aspects of GMANOVA, pointing to applications in various experimental settings, is given in [a21].
The general GMANOVA model was first stated in [a42], where the motivation was the modelling of experiments on the comparison of growth curves in different populations. Suppose such a growth curve can be represented by a polynomial in the time 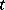 , say
, say 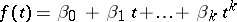 . If measurements are made on an individual at times
. If measurements are made on an individual at times 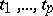 , then these
, then these 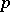 data are thought of as one observation on a
data are thought of as one observation on a 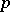 -variate population with population mean
-variate population with population mean 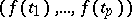 and covariance matrix
and covariance matrix 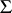 , where the
, where the 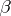 s and
s and 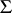 are unknown parameters. Suppose
are unknown parameters. Suppose 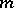 populations are to be compared and a sample of size
populations are to be compared and a sample of size 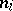 is taken from the
is taken from the 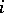 th population,
th population, 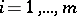 . In order to model this by (a3), let the
. In order to model this by (a3), let the  th column of
th column of 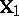 (corresponding to the
(corresponding to the 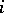 th population) have
th population) have 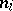
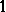 s, and
s, and  s otherwise. Specifically, the first column has a
s otherwise. Specifically, the first column has a 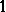 in positions
in positions 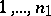 , the second in positions
, the second in positions 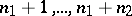 , etc.; then
, etc.; then 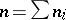 . Let the growth curve in the
. Let the growth curve in the 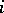 th population be
th population be 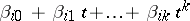 ; then the matrix
; then the matrix 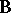 has
has 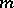 rows, the
rows, the 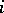 th row being
th row being 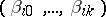 , so that
, so that 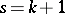 in (a3); and
in (a3); and 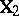 has
has 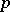 columns, the
columns, the 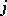 th one being
th one being 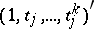 . (In the example given in [a42], measurements were taken at ages 8, 10, 12, and 14 in a group of girls and a group of boys; each measurement was of a certain distance between two points inside the head (with help of an X-ray picture) that is of interest in orthodontistry to monitor growth.)
. (In the example given in [a42], measurements were taken at ages 8, 10, 12, and 14 in a group of girls and a group of boys; each measurement was of a certain distance between two points inside the head (with help of an X-ray picture) that is of interest in orthodontistry to monitor growth.)
Linear hypotheses are in general of the form (a9). For instance, suppose two growth curves are to be compared, both assumed to be straight lines (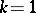 ) so that
) so that 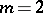 ,
, 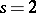 . Suppose the hypothesis is
. Suppose the hypothesis is 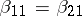 (equal slope in the two populations). Then in (a9) one can take
(equal slope in the two populations). Then in (a9) one can take 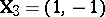 and
and 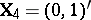 . Other examples of GMANOVA may be found in [a21].
. Other examples of GMANOVA may be found in [a21].
A canonical form for the GMANOVA model was derived in [a13]; it can also be found in [a21], Sect. 3.2. It can be obtained from the canonical form of MANOVA by partitioning the matrices 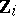 columnwise into three blocks, resulting in
columnwise into three blocks, resulting in 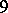 matrices
matrices 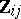 ,
, 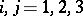 . Invariance reduction eliminates all
. Invariance reduction eliminates all 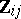 except
except 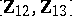 and
and 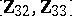 (the latter is used for estimating the relevant portion of the unknown covariance matrix
(the latter is used for estimating the relevant portion of the unknown covariance matrix 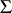 ). It is given that
). It is given that 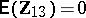 and
and 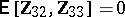 ; inference is desired on
; inference is desired on 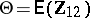 , e.g., to test the hypothesis
, e.g., to test the hypothesis 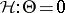 . Further sufficiency reduction leads to two matrix-valued statistics
. Further sufficiency reduction leads to two matrix-valued statistics 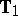 and
and 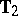 ([a20], [a21]), of which
([a20], [a21]), of which 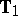 is the most important and is built-up from the following statistic:
is the most important and is built-up from the following statistic:
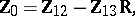 | (a10) |
in which 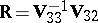 (with
(with  ) is the estimated regression of
) is the estimated regression of 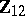 on
on 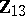 , the true regression being
, the true regression being 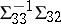 . That inference on
. That inference on 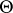 should be centred on
should be centred on 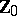 can be understood intuitively by realizing that if
can be understood intuitively by realizing that if 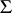 were known, then
were known, then 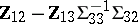 minimizes the variances among all linear combinations of
minimizes the variances among all linear combinations of 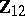 and
and 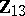 whose mean is
whose mean is  , and provides therefore better inference than using only
, and provides therefore better inference than using only 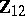 . The unknown regression is then estimated by
. The unknown regression is then estimated by 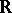 , leading to
, leading to 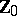 of (a10).
of (a10).
The essential difference between GMANOVA and MANOVA lies in the presence of 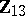 , which is correlated with
, which is correlated with 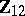 and has zero mean. Then
and has zero mean. Then 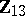 is used as a covariate for
is used as a covariate for 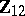 ; see, e.g., [a33]. However, not all models that appear to be GMANOVA produce such a covariate. More precisely, if in (a3)
; see, e.g., [a33]. However, not all models that appear to be GMANOVA produce such a covariate. More precisely, if in (a3) 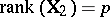 , then it turns out that in the canonical form there are no matrices
, then it turns out that in the canonical form there are no matrices 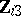 and the model reduces essentially to MANOVA. This situation was encountered previously when it was pointed out that the MANOVA model (a2) together with the GMANOVA-type hypothesis (a9) was immediately reducible to straight MANOVA. The same conclusion would have been reached after treating (a2), (a9) as a special case of GMANOVA and inspecting the canonical form. For a "true" GMANOVA the existence of
and the model reduces essentially to MANOVA. This situation was encountered previously when it was pointed out that the MANOVA model (a2) together with the GMANOVA-type hypothesis (a9) was immediately reducible to straight MANOVA. The same conclusion would have been reached after treating (a2), (a9) as a special case of GMANOVA and inspecting the canonical form. For a "true" GMANOVA the existence of 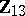 is essential. A typical example of true GMANOVA, where the covariate data are built into the experiment, was given in [a7].
is essential. A typical example of true GMANOVA, where the covariate data are built into the experiment, was given in [a7].
Inference on 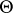 can proceed using only
can proceed using only 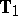 (e.g., [a27], and [a13]), but is not necessarily the best possible. For testing
(e.g., [a27], and [a13]), but is not necessarily the best possible. For testing 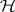 an essentially complete class of tests include those that also involve
an essentially complete class of tests include those that also involve 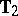 explicitly. One such test is the locally most-powerful test derived in [a20]. For the distribution theory of
explicitly. One such test is the locally most-powerful test derived in [a20]. For the distribution theory of 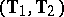 see [a21], Sect. 3.6, and [a54], Sect. 6.5. Admissibility and inadmissibility results were obtained in [a32]; comparison of various tests can also be found there. A natural estimator of
see [a21], Sect. 3.6, and [a54], Sect. 6.5. Admissibility and inadmissibility results were obtained in [a32]; comparison of various tests can also be found there. A natural estimator of 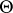 is
is 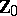 of (a10); it is an unbiased estimator and in [a22] it is shown to be best equivariant. Other kinds of estimators have also been considered, e.g., in [a24], in which several references to earlier work can be found. Simultaneous confidence intervals and sets have been treated in [a16], [a17], [a27], and [a28]. Special structures of the covariance matrix
of (a10); it is an unbiased estimator and in [a22] it is shown to be best equivariant. Other kinds of estimators have also been considered, e.g., in [a24], in which several references to earlier work can be found. Simultaneous confidence intervals and sets have been treated in [a16], [a17], [a27], and [a28]. Special structures of the covariance matrix 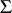 have been studied in [a44], where also references to earlier work on related topics can be found.
have been studied in [a44], where also references to earlier work on related topics can be found.
Generalizations.
A natural generalization of the GMANOVA model is indicated in [a13] by having a further partitioning of the blocks of 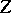 s in the canonical form. This is called extended GMANOVA in [a21] and examples are given there. Another generalization involves some relaxation of the usual assumptions of multivariate normality, etc. See [a23], [a12], [a17].
s in the canonical form. This is called extended GMANOVA in [a21] and examples are given there. Another generalization involves some relaxation of the usual assumptions of multivariate normality, etc. See [a23], [a12], [a17].
References
| [a1] | T.W. Anderson, "An introduction to multivariate statistical analysis" , Wiley (1984) (Edition: Second) |
| [a2] | T.W. Anderson, "The asymptotic distribution of characteristic roots and vectors in multivariate components of variance" L.J. Gleser (ed.) M.D. Perlman (ed.) S.J. Press (ed.) A.R. Sampson (ed.) , Contributions to Probability and Statistics; Essays in Honor of Ingram Olkin , Springer (1989) pp. 177–196 |
| [a3] | S.A. Andersson, M.D. Perlman, "Lattice-ordered conditional independence models for missing data" Statist. Prob. Lett. , 12 (1991) pp. 465–486 |
| [a4] | S.A. Andersson, M.D. Perlman, "Lattice models for conditional independence in a multivariate normal distribution" Ann. Statist. , 21 (1993) pp. 1318–1358 |
| [a5] | S.A. Andersson, J.I. Marden, M.D. Perlman, "Totally ordered multivariate linear models" Sankhyā A , 55 (1993) pp. 370–394 |
| [a6] | Y.M.M. Bishop, S.E. Fienberg, P.W. Holland, "Discrete multivariate analysis: Theory and practice" , MIT (1975) |
| [a7] | W.G. Cochran, C.I. Bliss, "Discrimination functions with covariance" Ann. Statist. , 19 (1948) pp. 151–176 |
| [a8] | M.L. Eaton, "Multivariate statistics, a vector space approach" , Wiley (1983) |
| [a9] | M.L. Eaton, T. Kariya, "Multivariate tests with incomplete data" Ann. Statist. , 11 (1983) pp. 654–665 |
| [a10] | S.E. Fienberg, "The analysis of cross-classified categorical data" , MIT (1980) (Edition: Second) |
| [a11] | K.R. Gabriel, "Simultaneous test procedures in multivariate analysis of variance" Biometrika , 55 (1968) pp. 489–504 |
| [a12] | N. Giri, K. Das, "On a robust test of the extended MANOVA problem in elliptically symmetric distributions" Sankhyā A , 50 (1988) pp. 234–248 |
| [a13] | L.J. Gleser, I. Olkin, "Linear models in multivariate analysis" R.C. Bose (ed.) , Essays in Probability and Statistics: In memory of S.N. Roy , Univ. North Carolina Press (1970) pp. 267–292 |
| [a14] | "Analysis of Variance" P.R. Krishnaiah (ed.) , Handbook of Statistics , 1 , North-Holland (1980) |
| [a15] | K. Hinkelmann, O. Kempthorne, "Design and analysis of experiments" , I: Introduction to experimental design , Wiley (1994) |
| [a16] | P.M. Hooper, "Simultaneous interval estimation in the general multivariate analysis of variance model" Ann. Statist. , 11 (1983) pp. 666–673 (Correction in: 12 (1984), 785) |
| [a17] | P.M. Hooper, W.K. Yau, "Optimal confidence regions in GMANOVA" Canad. J. Statist. , 14 (1986) pp. 315–322 |
| [a18] | D.R. Jensen, L.S. Mayer, "Some variational results and their applications in multiple inference" Ann. Statist. , 5 (1977) pp. 922–931 |
| [a19] | R.A. Johnson, D.W. Wichern, "Applied multivariate statistical analysis" , Prentice-Hall (1988) (Edition: Second) |
| [a20] | T. Kariya, "The general MANOVA problem" Ann. Statist. , 6 (1978) pp. 200–214 |
| [a21] | T. Kariya, "Testing in the multivariate general linear model" , Kinokuniya (1985) |
| [a22] | T. Kariya, "Equivariant estimation in a model with an ancillary statistic" Ann. Statist. , 17 (1989) pp. 920–928 |
| [a23] | T. Kariya, B.K. Sinha, "Robustness of statistical tests" , Acad. Press (1989) |
| [a24] | T. Kariya, Y. Konno, W.E. Strawderman, "Double shrinkage estimators in the GMANOVA model" J. Multivar. Anal. , 56 (1996) pp. 245–258 |
| [a25] | T. Kariya, P.R. Krishnaiah, C.R. Rao, "Statistical inference from multivariate normal populations when some data is missing" P.R. Krishnaiah (ed.) , Developm. in Statist. , 4 , Acad. Press (1983) pp. 137–148 |
| [a26] | O. Kempthorne, "The design and analysis of experiments" , Wiley (1952) |
| [a27] | C.G. Khatri, "A note on a MANOVA model applied to problems in growth curves" Ann. Inst. Statist. Math. , 18 (1966) pp. 75–86 |
| [a28] | P.R. Krishnaiah, "Simultaneous test procedures under general MANOVA models" P.R. Krishnaiah (ed.) , Multivariate Analysis II , Acad. Press (1969) pp. 121–143 |
| [a29] | A.M. Kshirsagar, "Multivariate analysis" , M. Dekker (1972) |
| [a30] | E.L. Lehmann, "Theory of point estimation" , Wiley (1983) |
| [a31] | E L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) (Edition: Second) |
| [a32] | J.I. Marden, "Admissibility of invariant tests in the general multivariate analysis of variance problem" Ann. Statist. , 11 (1983) pp. 1086–1099 |
| [a33] | J.I. Marden, M.D. Perlman, "Invariant tests for means with covariates" Ann. Statist. , 8 (1980) pp. 25–63 |
| [a34] | J.I. Marden, M.D. Perlman, "On the inadmissibility of step-down procedures for the Hotelling 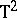 problem" Ann. Statist. , 18 (1990) pp. 172–190 problem" Ann. Statist. , 18 (1990) pp. 172–190 |
| [a35] | T. Mathew, A. Niyogi, B.K. Sinha, "Improved nonnegative estimation of variance components in balanced multivariate mixed models" J. Multivar. Anal. , 51 (1994) pp. 83–101 |
| [a36] | D.F. Morrison, "Multivariate statistical methods" , McGraw-Hill (1976) (Edition: Second) |
| [a37] | G.S. Mudholkar, "On confidence bounds associated with multivariate analysis of variance and non-independence between two sets of variates" Ann. Math. Statist. , 37 (1966) pp. 1736–1746 |
| [a38] | G.S. Mudholkar, P. Subbaiah, "A review of step-down procedures for multivariate analysis of variance" R.P. Gupta (ed.) , Multivariate Statistical Analysis , North-Holland (1980) pp. 161–178 |
| [a39] | G.S. Mudholkar, P. Subbaiah, "Some simple optimum tests in multivariate analysis" A.K. Gupta (ed.) , Advances in Multivariate Statistical Analysis , Reidel (1987) pp. 253–275 |
| [a40] | G.S. Mudholkar, P. Subbaiah, "On a Fisherian detour of the step-down procedure for MANOVA" Commun. Statist. Theory and Methods , 17 (1988) pp. 599–611 |
| [a41] | R.J. Muirhead, "Aspects of multivariate statistical theory" , Wiley (1982) |
| [a42] | R.F. Potthoff, S.N. Roy, "A generalized multivariate analysis of variance model useful especially for growth curve models" Biometrika , 51 (1964) pp. 313–326 |
| [a43] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1973) (Edition: Second) |
| [a44] | C.R. Rao, "Least squares theory using an estimated dispersion matrix and its application to measurement of signals" L.M. Le Cam (ed.) J. Neyman (ed.) , Fifth Berkeley Symp. Math. Statist. Probab. , 1 , Univ. California Press (1967) pp. 355–372 |
| [a45] | C.R. Rao, S.K. Mitra, "Generalized inverses of matrices and its applications" , Wiley (1971) |
| [a46] | S.N. Roy, R.C. Bose, "Simultaneous confidence interval estimation" Ann. Math. Statist. , 24 (1953) pp. 513–536 |
| [a47] | H. Scheffé, "Alternative models for the analysis of variance" Ann. Math. Statist. , 27 (1956) pp. 251–271 |
| [a48] | H. Scheffé, "The analysis of variance" , Wiley (1959) |
| [a49] | S.R. Searle, "Linear models" , Wiley (1971) |
| [a50] | S.R. Searle, "Linear models for unbalanced data" , Wiley (1987) |
| [a51] | S. Weisberg, "Applied linear regression" , Wiley (1985) (Edition: Second) |
| [a52] | R.A. Wijsman, "Constructing all smallest simultaneous confidence sets in a given class, with applications to MANOVA" Ann. Statist. , 7 (1979) pp. 1003–1018 |
| [a53] | R.A. Wijsman, "Smallest simultaneous confidence sets with applications in multivariate analysis" P.R. Krishnaiah (ed.) , Multivariate Analysis V , North-Holland (1980) pp. 483–498 |
| [a54] | R.A. Wijsman, "Global cross sections as a tool for factorization of measures and distribution of maximal invariants" Sankhyā A , 48 (1986) pp. 1–42 |
| [a55] | R.A. Wijsman, "Invariant measures on groups and their use in statistics" , Lecture Notes Monograph Ser. , 14 , Inst. Math. Statist. (1990) |
| [a56] | "Encyclopedia of Statistical Sciences" S. Kotz (ed.) N.L. Johnson (ed.) , Wiley (1982/88) |
ANOVA. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=ANOVA&oldid=14171