A-system
A "countably-ramified" system of sets, i.e. a family  of subsets of a set
of subsets of a set 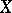 , indexed by all finite sequences of natural numbers. An
, indexed by all finite sequences of natural numbers. An  -system
-system  is called regular if
is called regular if 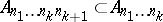 . A sequence
. A sequence 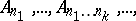 of elements of an
of elements of an 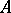 -system indexed by all segments of one and the same finite sequence of natural numbers is called a chain of this
-system indexed by all segments of one and the same finite sequence of natural numbers is called a chain of this 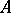 -system. The intersection of all elements of a chain is called its kernel, and the union of all kernels of all chains of an
-system. The intersection of all elements of a chain is called its kernel, and the union of all kernels of all chains of an  -system is called the kernel of this
-system is called the kernel of this 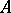 -system, or the result of the
-system, or the result of the 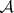 -operation applied to this
-operation applied to this  -system, or the
-system, or the  -set generated by this
-set generated by this 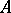 -system. Every
-system. Every 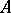 -system can be regularized without changing the kernel (it suffices to put
-system can be regularized without changing the kernel (it suffices to put 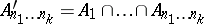 ). If
). If 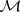 is a system of sets, then the kernels of the
is a system of sets, then the kernels of the 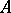 -system composed from the elements of
-system composed from the elements of 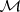 are called the
are called the 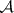 -sets generated by
-sets generated by 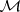 . The
. The 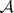 -sets generated by the closed sets of a topological space are called the
-sets generated by the closed sets of a topological space are called the 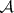 -sets of this space.
-sets of this space.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | K. Kuratowski, "Topology" , 1 , Acad. Press (1966) (Translated from French) |
Comments
The 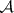 -operation is an important tool in descriptive set theory. It was introduced by M.Ya. Suslin, hence it is also known as the Suslin operation (also Souslin operation). In this connection, an
-operation is an important tool in descriptive set theory. It was introduced by M.Ya. Suslin, hence it is also known as the Suslin operation (also Souslin operation). In this connection, an 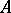 -system is also called a Suslin (Souslin) scheme. See also
-system is also called a Suslin (Souslin) scheme. See also  -operation;
-operation; 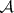 -set.
-set.
While [2] is the standard reference for classical results, a modern approach can be found in [a1].
References
| [a1] | J.P.R. Christensen, "Topology and Borel structure" , North-Holland (1974) |
A-system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=A-system&oldid=14440