Difference between revisions of "*-Autonomous category"
From Encyclopedia of Mathematics
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 19 formulas, 17 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Let $\mathcal{C}$ be a symmetric [[Closed monoidal category|closed monoidal category]] (cf. also [[Category|Category]]). A [[Functor|functor]] $( - ) ^ { * } : \cal C ^ { \operatorname{op} } \rightarrow C$ is a duality functor if there exists an isomorphism $d ( A , B ) : B ^ { A } \overset{\cong}{\rightarrow} A ^ { * } B ^ { * }$, natural in $A$ and $B$, such that for all objects $A , B , C \in \mathcal{C}$ the following diagram commutes: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130010/a1300108.png"/></td> </tr></table> | |
| − | + | where in the bottom arrow $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$. | |
| − | + | A category is $*$-autonomous if it is a symmetric monoidal closed category with a given duality functor. | |
| − | From a given symmetric monoidal closed category and an object in it (that serves as a dualizing object) one can construct a | + | It so happens that $*$-autonomous categories have real-life applications: they are models of (at least the finite part of) linear logic [[#References|[a2]]] and have uses in modelling processes. |
| + | |||
| + | An example of a $*$-autonomous category is the category $\mathcal{R} \text{el}$ of sets and relations; duality is given by $S ^ { * } = S$. In fact, $B ^ { A } \cong ( A ^ { * } \otimes B )$. | ||
| + | |||
| + | From a given symmetric monoidal closed category and an object in it (that serves as a dualizing object) one can construct a $*$-autonomous category (the so-called Chu construction, [[#References|[a3]]]). It can be viewed as a kind of generalized topology. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> M. Barr, "$*$-Autonomous categories" , ''Lecture Notes in Mathematics'' , '''752''' , Springer (1979)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> M. Barr, C. Wells, "Category theory for computing science" , Publ. CRM (1990)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> P.-H. Chu, "Constructing $*$-autonomous categories" M. Barr (ed.) , ''$*$-Autonomous categories'' , ''Lecture Notes in Mathematics'' , '''752''' , Springer (1979) pp. Appendix</td></tr></table> |
Latest revision as of 17:46, 1 July 2020
Let $\mathcal{C}$ be a symmetric closed monoidal category (cf. also Category). A functor $( - ) ^ { * } : \cal C ^ { \operatorname{op} } \rightarrow C$ is a duality functor if there exists an isomorphism $d ( A , B ) : B ^ { A } \overset{\cong}{\rightarrow} A ^ { * } B ^ { * }$, natural in $A$ and $B$, such that for all objects $A , B , C \in \mathcal{C}$ the following diagram commutes:
 |
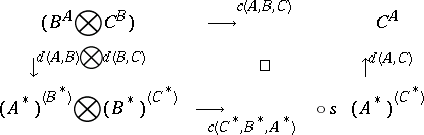where in the bottom arrow $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$.
A category is $*$-autonomous if it is a symmetric monoidal closed category with a given duality functor.
It so happens that $*$-autonomous categories have real-life applications: they are models of (at least the finite part of) linear logic [a2] and have uses in modelling processes.
An example of a $*$-autonomous category is the category $\mathcal{R} \text{el}$ of sets and relations; duality is given by $S ^ { * } = S$. In fact, $B ^ { A } \cong ( A ^ { * } \otimes B )$.
From a given symmetric monoidal closed category and an object in it (that serves as a dualizing object) one can construct a $*$-autonomous category (the so-called Chu construction, [a3]). It can be viewed as a kind of generalized topology.
References
| [a1] | M. Barr, "$*$-Autonomous categories" , Lecture Notes in Mathematics , 752 , Springer (1979) |
| [a2] | M. Barr, C. Wells, "Category theory for computing science" , Publ. CRM (1990) |
| [a3] | P.-H. Chu, "Constructing $*$-autonomous categories" M. Barr (ed.) , $*$-Autonomous categories , Lecture Notes in Mathematics , 752 , Springer (1979) pp. Appendix |
How to Cite This Entry:
*-Autonomous category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-Autonomous_category&oldid=12194
*-Autonomous category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=*-Autonomous_category&oldid=12194
This article was adapted from an original article by Michel Eytan (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article