Birch-Tate conjecture
Let 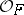 be the ring of integers of an algebraic number field
be the ring of integers of an algebraic number field 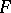 (cf. also Algebraic number). The Milnor
(cf. also Algebraic number). The Milnor 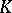 -group
-group 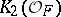 , which is also called the tame kernel of
, which is also called the tame kernel of 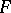 , is an Abelian group of finite order.
, is an Abelian group of finite order.
Let 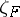 denote the Dedekind zeta-function of
denote the Dedekind zeta-function of 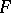 . If
. If 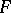 is totally real, then
is totally real, then 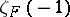 is a non-zero rational number, and the Birch–Tate conjecture is about a relationship between
is a non-zero rational number, and the Birch–Tate conjecture is about a relationship between 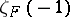 and the order of
and the order of 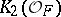 .
.
Specifically, let 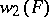 be the largest natural number
be the largest natural number 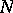 such that the Galois group of the cyclotomic extension over
such that the Galois group of the cyclotomic extension over 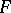 obtained by adjoining the
obtained by adjoining the 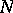 th roots of unity to
th roots of unity to 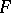 , is an elementary Abelian
, is an elementary Abelian  -group (cf.
-group (cf. 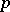 -group). Then
-group). Then 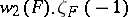 is a rational integer, and the Birch–Tate conjecture states that if
is a rational integer, and the Birch–Tate conjecture states that if 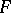 is a totally real number field, then
is a totally real number field, then
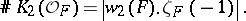 |
A numerical example is as follows. For 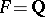 one has
one has 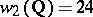 ,
, 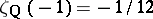 ; so it is predicted by the conjecture that the order of
; so it is predicted by the conjecture that the order of 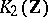 is
is  , which is correct.
, which is correct.
What is known for totally real number fields 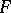 ?
?
By work on the main conjecture of Iwasawa theory [a6], the Birch–Tate conjecture was confirmed up to  -torsion for Abelian extensions
-torsion for Abelian extensions 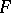 of
of 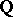 .
.
Subsequently, [a7], the Birch–Tate conjecture was confirmed up to  -torsion for arbitrary totally real number fields
-torsion for arbitrary totally real number fields 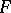 .
.
Moreover, [a7] (see the footnote on page 499) together with [a4], also the  -part of the Birch–Tate conjecture is confirmed for Abelian extensions
-part of the Birch–Tate conjecture is confirmed for Abelian extensions 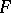 of
of 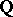 .
.
By the above, all that is left to be considered is the  -part of the Birch–Tate conjecture for non-Abelian extensions
-part of the Birch–Tate conjecture for non-Abelian extensions 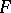 of
of 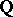 . In this regard, for extensions
. In this regard, for extensions 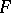 of
of 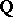 for which the
for which the  -primary subgroup of
-primary subgroup of 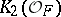 is elementary Abelian, the
is elementary Abelian, the  -part of the Birch–Tate conjecture has been confirmed [a3].
-part of the Birch–Tate conjecture has been confirmed [a3].
In addition, explicit examples of families of non-Abelian extensions 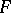 of
of 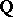 for which the
for which the  -part of the Birch–Tate conjecture holds, have been given in [a1], [a2].
-part of the Birch–Tate conjecture holds, have been given in [a1], [a2].
The Birch–Tate conjecture is related to the Lichtenbaum conjectures [a5] for totally real number fields 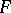 . For every odd natural number
. For every odd natural number 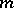 , the Lichtenbaum conjectures express, up to
, the Lichtenbaum conjectures express, up to  -torsion, the ratio of the orders of
-torsion, the ratio of the orders of 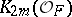 and
and 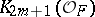 in terms of the value of the zeta-function
in terms of the value of the zeta-function 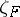 at
at 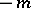 .
.
References
| [a1] | P.E. Conner, J. Hurrelbrink, "Class number parity" , Pure Math. , 8 , World Sci. (1988) |
| [a2] | J. Hurrelbrink, "Class numbers, units, and  " J.F. Jardine (ed.) V. Snaith (ed.) , Algebraic " J.F. Jardine (ed.) V. Snaith (ed.) , Algebraic 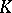 -theory: Connection with Geometry and Topology , NATO ASI Ser. C , 279 , Kluwer Acad. Publ. (1989) pp. 87–102 -theory: Connection with Geometry and Topology , NATO ASI Ser. C , 279 , Kluwer Acad. Publ. (1989) pp. 87–102 |
| [a3] | M. Kolster, "The structure of the  -Sylow subgroup of -Sylow subgroup of 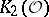 I" Comment. Math. Helv. , 61 (1986) pp. 376–388 I" Comment. Math. Helv. , 61 (1986) pp. 376–388 |
| [a4] | M. Kolster, "A relation between the  -primary parts of the main conjecture and the Birch–Tate conjecture" Canad. Math. Bull. , 32 : 2 (1989) pp. 248–251 -primary parts of the main conjecture and the Birch–Tate conjecture" Canad. Math. Bull. , 32 : 2 (1989) pp. 248–251 |
| [a5] | S. Lichtenbaum, "Values of zeta functions, étale cohomology, and algebraic 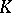 -theory" H. Bass (ed.) , Algebraic -theory" H. Bass (ed.) , Algebraic 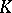 -theory II , Lecture Notes in Mathematics , 342 , Springer (1973) pp. 489–501 -theory II , Lecture Notes in Mathematics , 342 , Springer (1973) pp. 489–501 |
| [a6] | B. Mazur, A. Wiles, "Class fields of abelian extensions of 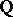 " Invent. Math. , 76 (1984) pp. 179–330 " Invent. Math. , 76 (1984) pp. 179–330 |
| [a7] | A. Wiles, "The Iwasawa conjecture for totally real fields" Ann. of Math. , 131 (1990) pp. 493–540 |
Birch-Tate conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Birch-Tate_conjecture&oldid=11217