Yang-Mills functional, geometry of the
The geometry of the Yang–Mills equations (cf. Yang–Mills field) led to deep purely mathematical insight, some of which is given below. For notations, see Yang–Mills functional.
A symplectic approach in terms of Yang–Mills theory for a bundle on a closed $2$-manifold enabled M.F. Atiyah and R. Bott [a1] to explain old results of M.S. Narasimhan and C.S. Seshadri on moduli spaces of stable holomorphic vector bundles on Riemann surfaces. Among others, Atiyah and Bott derived formulas for the Betti numbers of these moduli spaces which had been obtained earlier by G. Harder and Narasimhan by number-theoretical methods. These moduli spaces carry additional geometrical structures, such as symplectic or, more generally, Poisson or even Kähler structures; see, e.g., [a1] or [a5]. An analogous formalism led to gauge-theoretic equations (now called Hermite–Einstein equations) whose solutions might be expected to exist on stable bundles over higher-dimensional Kähler manifolds. Much research on the Narasimhan–Seshadri moduli spaces is still (1998) going on, e.g. on the ring structure of their real cohomology; see, e.g., [a6] for more details and references.
Spectacular results in the topology of $4$-manifolds have been obtained by S.K. Donaldson: Consider a principal $G$-bundle $\xi $ on an oriented Riemannian $4$-manifold $M$, for a compact Lie group $G$ with an invariant scalar product on its Lie algebra. The connections of interest are the so-called instantons, the solutions of the anti-self-dual Yang–Mills equation
\begin{equation*} ^ { * } F _ { A } = - F _ { A }. \end{equation*}
When $G$ is the circle group, the anti-self-duality equation is linear and the instantons are completely described by Hodge theory. When $G$ is $\operatorname{SU} ( 2 )$ (say), the equation is a non-linear partial differential equation. Its space of solutions, the moduli space of instantons modulo gauge transformations, is generically (that is, for a generic choice of the metric on $M$) a finite-dimensional smooth manifold which is usually non-compact. In 1981, Donaldson had the insight that the algebraic topology of this moduli space could be used to analyze the topology of the manifold $M$ itself. This came as a complete surprise, since there was no conceptual understanding of how and why instantons were related to the structure of $4$-manifolds. Donaldson first discovered restrictions on the intersection form of a compact $4$-manifold and deduced that certain topological $4$-manifolds do not support any differentiable structure at all. Later he defined differentiable invariants of large classes of manifolds, nowadays called Donaldson polynomials, which were successful in distinguishing non-diffeomorphic differentiable structures on $4$-manifolds. This prompted an entirely new research area. See [a3] for details.
In 1994, this research area was turned on its head by the introduction of a new kind of gauge theory, phrased in terms of the differential-geometric equation by N. Seiberg and E. Witten, which, in turn, had again originated from physics, more precisely, from supersymmetry considerations in quantum field theory. Some long-standing problems were solved. For example, P.B. Kronheimer and T.S. Mrowka solved the so-called Thom conjecture that algebraic curves should minimize the genus within a given homology class in $\mathbf{CP} ^ { 2 }$. Also, new and unexpected results were found, e.g. C. Taubes established the non-existence of symplectic structures on certain $4$-manifolds and linked Seiberg–Witten invariants of symplectic manifolds with Gromov invariants, as well as gave simpler new proofs for existing results. The Seiberg–Witten equations involve two entities, a $U ( 1 )$-connection and a spinor field, the most relevant notion being that of a 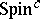 -structure on an oriented Riemannian $4$-manifold $M$. Associated with a
-structure on an oriented Riemannian $4$-manifold $M$. Associated with a 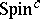 structure on $M$ are bundles $V _ { \pm }$ of positive and negative spinors, a complex determinant line bundle $L = \operatorname { det } ( V _ { \pm } )$ and, furthermore, a canonical mapping $\sigma$ from $V _ { + } \times V _ { + }$ to $\Lambda _ { + } ^ { 2 }$. The equations involve a connection $A$ and a positive spinor $\phi \in \Gamma ( V _ { + } )$ and read
structure on $M$ are bundles $V _ { \pm }$ of positive and negative spinors, a complex determinant line bundle $L = \operatorname { det } ( V _ { \pm } )$ and, furthermore, a canonical mapping $\sigma$ from $V _ { + } \times V _ { + }$ to $\Lambda _ { + } ^ { 2 }$. The equations involve a connection $A$ and a positive spinor $\phi \in \Gamma ( V _ { + } )$ and read
\begin{equation*} D _ { A } \phi = 0, \end{equation*}
\begin{equation*} F _ { A } ^ { + } = i \sigma ( \phi , \phi ); \end{equation*}
here, $D _ { A }$ is the Dirac operator $D _ { A } : \Gamma ( V _ { + } ) \rightarrow \Gamma ( V _ { - } )$ arising from composition of the covariant derivative with Clifford multiplication. The solutions of these equations (these are certain monopoles) are the absolute minima of a certain functional, much as the Yang–Mills instantons minimize the ordinary Yang–Mills functional. The moduli space of these monopoles modulo bundle automorphisms is generically a smooth manifold and it is always compact. The compactness makes these spaces much easier to handle than the instanton moduli spaces. See [a2] and [a7] for more details and references.
Many other aspects, for example links to Yang–Mills–Higgs bundles and Floer theory, have been omitted here; see, e.g., the cited references.
References
| [a1] | M.F. Atiyah, R. Bott, "The Yang–Mills equations over Riemann surfaces" Philos. Trans. R. Soc. London A , 308 (1982) pp. 523–615 |
| [a2] | S.K. Donaldson, "The Seiberg–Witten equations and $4$-manifold topology" Bull. Amer. Math. Soc. , 33 (1996) pp. 45–70 |
| [a3] | S.K. Donaldson, P.B. Kronheimer, "The geometry of four–manifolds" , Oxford Univ. Press (1991) |
| [a4] | N.J. Hitchin, "Book reviews. T. Petrie and J. Randall: Connections, definite forms, and four–manifolds; S.K. Donaldson and P.B. Kronheimer: The geometry of four-manifolds" Bull. London Math. Soc. , 25 (1993) pp. 499–502 |
| [a5] | J. Huebschmann, "Poisson geometry of certain moduli spaces" , Lectures 14th Winter School, Srni, Czeque Republic, Jan. 1994 Rend. Circ. Mat. Palermo, Ser. II , 39 (1996) pp. 15–35 |
| [a6] | J. Huebschmann, "Review on a paper by L. Jeffrey and F. Kirwan" Math. Reviews , 98e (1998) pp. 58088 |
| [a7] | D. Kotschik, "Gauge theory is dead! — long live gauge theory" Notices Amer. Math. Soc. , 42 (1995) pp. 335–338 |
Yang-Mills functional, geometry of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Yang-Mills_functional,_geometry_of_the&oldid=50726