Witt algebra
Let $ k $
be a field of characteristic $ p \neq 0 $.
Consider the $ k $-
algebra
$$ A _ {n} = k [ X _ {1} \dots X _ {n} ] / ( X _ {1} ^ {p} \dots X _ {n} ^ {p} ) . $$
Let $ V _ {n} $ be the algebra of $ k $- derivations of $ A _ {n} $. The algebra $ V _ {1} $ is known as the Witt algebra. The $ V _ {n} $( $ n \geq 2 $) are known as the split Jacobson–Witt algebras. The algebra $ V _ {n} $ is a simple Lie algebra, except when it is $ 2 $- dimensional. The dimension of $ V _ {n} $ is $ np ^ {n} $.
More generally one considers the $ k $- algebras
$$ A _ {n} ( \xi ) = k [ X _ {1} \dots X _ {n} ] / ( X _ {1} ^ {p} - \xi _ {1} \dots X _ {n} ^ {p} - \xi _ {n} ) , $$
and their algebras of derivations $ V _ {n} ( \xi ) $, the Jacobson–Witt algebras. The $ A _ {n} ( \xi ) $ and $ V _ {n} ( \xi ) $ are (obviously) $ k ^ \prime / k $- forms of $ A _ {n} $ and $ V _ {n} $, where $ k ^ \prime = k ( \xi _ {1} ^ {1/p} \dots \xi _ {n} ^ {1/p} ) $( cf. Form of an (algebraic) structure). Many simple Lie algebras in characteristic $ p $ arise as subalgebras of the $ V _ {n} $.
Let $ G $ be an additive group of functions on $ \{ 1 \dots m \} $ into $ k $ such that the only element $ f $ of $ G $ such that $ \sum f( i) g( i) = 0 $ for all $ g \in G $ is the zero element $ f = 0 $. For instance, $ G $ can be the set of all functions from $ \{ 1 \dots m \} $ to some additive subgroup of $ k $. If $ G $ is finite, it is of order $ p ^ {n} $ for some $ n $. Now, let $ V $ be a vector space over $ k $ with basis elements $ e _ {g} ^ {i} $, $ i = 1 \dots m $, $ g \in G $, and define a bilinear product on $ V $ by
$$ [ e _ {g} ^ {i} , e _ {h} ^ {j} ] = \ h( i) e _ {g+ h } ^ {j} - g( j) e _ {g+ h } ^ {i} . $$
There results a Lie algebra, called a generalized Witt algebra. If $ G $ is finite of order $ p ^ {n} $, the dimension of $ V $ is $ m p ^ {n} $, and $ V $ is a simple Lie algebra if $ m > 1 $ or $ p > 2 $.
If $ k $ is of characteristic zero, $ m = 1 $ and $ G $ is the additive subgroup $ \mathbf Z \subset k $, the same construction results in the Virasoro algebra $ [ e _ {g} , e _ {h} ] = ( h- g) e _ {g+} h $.
If $ k $ is of characteristic $ p $ and $ G $ is the group of all functions on $ \{ 1 \dots n \} $ with values in $ \mathbf Z / ( p) \subset k $, one recovers the Jacobson–Witt algebras $ V _ {n} $.
There are no isomorphisms between the Jacobson–Witt algebras $ V _ {n} $ and the classical Lie algebras in positive characteristic when $ \mathop{\rm char} ( k) \neq 2, 3 $. Several more classes of simple Lie algebras different from the classical ones and the $ V _ {n} $ are known, [a1].
The Witt algebra(s) described here should of course not be confused with the Witt ring of quadratic forms over a field, nor with the various rings of Witt vectors, cf. Witt vector.
References
| [a1] | G.B. Seligman, "Modular Lie algebras" , Springer (1967) MR0245627 Zbl 0189.03201 |
| [a2] | N. Jacobson, "Classes of restricted Lie algebras of characteristic 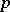 , II" Duke Math. J. , 10 (1943) pp. 107–121 , II" Duke Math. J. , 10 (1943) pp. 107–121 |
| [a3] | R. Ree, "On generalised Witt algebras" Trans. Amer. Math. Soc. , 83 (1956) pp. 510–546 |
Witt algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witt_algebra&oldid=49231