Wild sphere
From Encyclopedia of Mathematics
A closed manifold in Euclidean three-space $E^3$ obtained by a wild imbedding of the sphere $S^2$ in $E^3$. Thus, a wild sphere is the sum of two discs with a common boundary, which is a wild knot. The first example of a wild sphere is the so-called "horned sphere of Alexander", horned sphere or Alexander sphere (Fig. a); it bounds a domain which is not homeomorphic to $E^3$ (in the figure this is the interior of the cylinder without any interlinking handles and points forming their boundary). Fig. b shows a wild sphere in which the exterior domain alone is not homeomorphic to $E^3$.
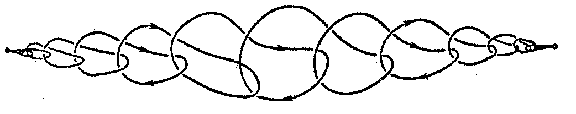
Figure: w097990a
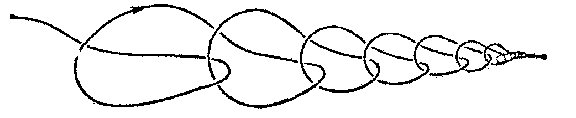
Figure: w097990b
References
| [1] | L.V. Keldysh, "Topological imbeddings in Euclidean space" Proc. Steklov Inst. Math. , 81 (1968) Trudy Mat. Inst. Akad. Nauk. SSSR , 81 (1966) |
| [a1] | R.H. Bing, "The geometric topology of $3$-manifolds" , Amer. Math. Soc. (1983) |
| [a2] | E.E. Moise, "Geometric topology in dimensions 2 and 3" , Springer (1977) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Wild sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_sphere&oldid=53888
Wild sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_sphere&oldid=53888
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article