Wiener-Itô decomposition
Itô–Wiener decomposition
An orthogonal decomposition of the Hilbert space of square-integrable functions on a Gaussian space. It was first proved in 1938 by N. Wiener [a6] in terms of homogeneous chaos (cf. also Wiener chaos decomposition). In 1951, K. Itô [a1] defined multiple Wiener integrals to interpret homogeneous chaos and gave a different proof of the decomposition theorem.
Take an abstract Wiener space $( H , B )$ [a3] (cf. also Wiener space, abstract). Let $\mu$ be the standard Gaussian measure on $B$. The abstract version of Wiener–Itô decomposition deals with a special orthogonal decomposition of the real Hilbert space $L ^ { 2 } ( \mu )$.
Each $h \in H$ defines a normal random variable $\tilde{h}$ on $B$ with mean $0$ and variance $| h | _ { H } ^ { 2 }$ [a3]. Let $F _ { 0 } = \mathbf{R}$. For $n \geq 1$, let $F _ { n }$ be the $L ^ { 2 } ( \mu )$-closure of the linear space spanned by $1$ and random variables of the form $\tilde { h } _ { 1 } \ldots \tilde { h } _ { k }$ with $k \leq n$ and $h _ { j } \in H$ for $1 \leq j \leq k$. Then $\{ F _ { n } \} _ { n = 0 } ^ { \infty }$ is an increasing sequence of closed subspaces of $L ^ { 2 } ( \mu )$. Let $G _ { 0 } = \mathbf{R}$ and, for $n \geq 1$, let $G_n$ be the orthogonal complement of $F _ { n-1 } $ in $F _ { n }$. The elements in $G_n$ are called homogeneous chaos of degree $n$. Obviously, the spaces $G_n$ are orthogonal. Moreover, the Hilbert space $L ^ { 2 } ( \mu )$ is the direct sum of $G_n$ for $n \geq 0$, namely, $L ^ { 2 } ( \mu ) = \sum _ { n = 0 } ^ { \infty } G _ { n }$.
Fix $n \geq 1$. To describe $G_n$ more precisely, let $P_n$ be the orthogonal projection of $L ^ { 2 } ( \mu )$ onto the space $G_n$. For $h _ { 1 } \otimes \ldots \otimes h _ { n } \in H ^ { \otimes n }$, define
\begin{equation*} \theta _ { n } ( h _ { 1 } \bigotimes \ldots \bigotimes h _ { n } ) = P _ { n } ( \tilde { h _ { 1 } } \ldots \tilde { h _ { n } } ). \end{equation*}
Then $\theta _ { n } ( h _ { 1 } \otimes \ldots \otimes h _ { n } ) = \theta _ { n } ( h _ { 1 } \otimes^\wedge \ldots \otimes^\wedge \sim h _ { n } )$ (where $\otimes\hat{}$ denotes the symmetric tensor product) and
\begin{equation*} \left\| \theta _ { n } ( h _ { 1 } \bigotimes \ldots \bigotimes h _ { n } ) \right\| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } \left| h _ { 1 } \widehat{\bigotimes} \ldots \widehat{\bigotimes} h _ { n } \right| _ { H ^{ \bigotimes n }}. \end{equation*}
Thus, $\theta _ { n }$ extends by continuity to a continuous linear operator from $H ^{\otimes n}$ into $G_n$ and is an isometric mapping (up to the constant $\sqrt { n ! }$) from $H ^ { \widehat{\otimes} n }$ into $G_n$. Actually, $\theta _ { n }$ is surjective and so for any $\varphi \in G _ { n }$, there exists a unique $f \in H ^ { \hat{\otimes} n }$ such that $\theta _ { n } ( f ) = \varphi$ and $\| \varphi \| _ { L ^ { 2 } ( \mu ) } = \sqrt { n ! } | f | _ { H ^ { \otimes n } }$. Therefore, for any $\varphi \in L ^ { 2 } ( \mu )$, there exists a unique sequence $\{ f _ { n } \} _ { n = 0 } ^ { \infty }$ with $f _ { n } \in H ^ { \widehat{ \otimes } n }$ such that
\begin{equation*} \varphi = \sum _ { n = 0 } ^ { \infty } \theta _ { n } ( f _ { n } ), \end{equation*}
\begin{equation*} \| \varphi \| _ { L ^ { 2 } ( \mu ) } ^ { 2 } = \sum _ { n = 0 } ^ { \infty } n ! | f _ { n } | ^ { 2 } _ { H ^ {\bigotimes n}}. \end{equation*}
This is the abstract version of the Wiener–Itô decomposition theorem [a2], [a4], [a5].
Let $\Gamma ( H ) = \sum _ { n = 0 } ^ { \infty } H ^ { \widehat{\otimes} n }$. Define a norm on $\Gamma ( H )$ by
\begin{equation*} \| ( f _ { 0 } , f _ { 1 } , \ldots ) \| _ { \Gamma ( H ) } = \left( \sum _ { n = 0 } ^ { \infty } n ! |f _ { n } | _ { H^{\bigotimes n} } ^ { 2 } \right) ^ { 1 / 2 }. \end{equation*}
The Hilbert space $\Gamma ( H )$ is called the Fock space of $H$ (cf. also Fock space). The spaces $\Gamma ( H )$ and $L ^ { 2 } ( \mu )$ are isomorphic under the unitary operator $\Theta$ defined by
\begin{equation*} \Theta ( f _ { 0 } , f _ { 1 } , \ldots ) = \sum _ { n = 0 } ^ { \infty } \theta _ { n } ( f _ { n } ). \end{equation*}
Let $\{ e _ { k } : k \geq 1 \}$ be an orthonormal basis (cf. also Orthogonal basis) for $H$. For any non-negative integers $n _ { 1 } , n _ { 2 } , \dots$ such that $n _ { 1 } + n _ { 2 } + \ldots = n$, define
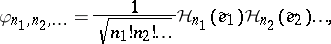 |
where $\mathcal{H} _ { k } ( x ) = ( - 1 ) ^ { n } e ^ { x ^ { 2 } / 2 } D _ { x } ^ { k } e ^ { - x ^ { 2 } / 2 }$ is the Hermite polynomial of degree $k$ (cf. also Hermite polynomials). The set $\{ \varphi _ { n _ { 1 } , n _ { 2 } , \ldots } : n _ { j } \geq 0 , n _ { 1 } + n _ { 2 } + \ldots = n \}$ is an orthonormal basis for the space $G_n$ of homogeneous chaos of degree $n$. Hence the set $\{ \varphi _ { n _ { 1 } , n _ { 2 } , \ldots } : n _ { j } \geq 0 , n _ { 1 } + n _ { 2 } + \ldots = n , n \geq 0 \}$ forms an orthonormal basis for $L ^ { 2 } ( \mu )$.
Consider the classical Wiener space $( C ^ { \prime } , C )$ [a3]. The Hilbert space $C ^ { \prime }$ is isomorphic to $L ^ { 2 } ( [ 0,1 ] )$ under the unitary operator $\iota( g ) = g ^ { \prime }$, $g \in C ^ { \prime }$. The standard Gaussian measure $\mu$ on $C$ is the Wiener measure and $B ( t , \omega ) = \omega ( t )$, $\omega \in C$, is a Brownian motion. For $g \in L ^ { 2 } ( [ 0,1 ] )$, the random variable $\widetilde{( \iota ^ { - 1 } g )}$ is exactly the Wiener integral $I ( g ) = \int _ { 0 } ^ { 1 } g ( t ) d B ( t )$. Let $g _ { j } \in L ^ { 2 } ( [ 0,1 ] )$, $1 \leq j \leq n$. The random variable
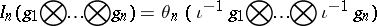 |
is a homogeneous chaos in the space $G_n$. The mapping $ { I } _ { n }$ extends by continuity to the space $L ^ { 2 } ( [ 0,1 ] ^ { n } )$. For $g \in L ^ { 2 } ( [ 0,1 ] ^ { n } )$,
\begin{equation*} I _ { n } ( g ) = \int _ { [ 0,1 ] ^ { n } } g ( t _ { 1 } , \ldots , t _ { n } ) d B ( t _ { 1 } ) \ldots d B ( t _ { n } ), \end{equation*}
where the right-hand side is a multiple Wiener integral of order $n$ as defined by Itô in [a1] and $\| I _ { n } ( g ) \| _ { L ^{ 2} ( \mu ) } = \sqrt { n ! } | \hat{g} | _ { L ^{ 2} ( [ 0,1 ] ^ { n } )}$ (where $\hat{g}$ is the symmetrization of $g$.) For any $\varphi \in L ^ { 2 } ( \mu )$ there exists a unique sequence $\{ g _ { n } \} _ { n = 0 } ^ { \infty }$ of symmetric functions $g _ { n } \in L ^ { 2 } ( [ 0,1 ] ^ { n } )$ such that
\begin{equation*} \varphi = \sum _ { n = 0 } ^ { \infty } I _ { n } ( g _ { n } ), \end{equation*}
\begin{equation*} \| \varphi \| _ { L ^ { 2 } ( \mu ) } ^ { 2 } = \sum _ { n = 0 } ^ { \infty } n ! | g _ { n } | _ { L^2 ( [ 0,1 ] ^ { n } ) } ^ { 2 } . \end{equation*}
This is the Wiener–Itô decomposition theorem in terms of multiple Wiener integrals. An orthonormal basis for $L ^ { 2 } ( \mu )$ is given by the set
\begin{equation*} \frac { 1 } { \sqrt { n _ { 1 } ! n _ { 2 } ! \ldots } }. \end{equation*}
\begin{equation*} .\mathcal{H} _ { n _ { 1 } } \left( \int _ { 0 } ^ { 1 } e _ { 1 } ( t ) d B ( t ) \right) \mathcal{H} _ { n _ { 2 } } \left( \int _ { 0 } ^ { 1 } e _ { 2 } ( t ) d B ( t ) \right) \ldots ,\; n _ { j } \geq 0 ,\; n _ { 1 } + n _ { 2 } + \ldots = n ,\; n \geq 0, \end{equation*}
where $\{ e _ { k } : k \geq 1 \}$ is an orthonormal basis for $L ^ { 2 } ( [ 0,1 ] )$ and the integrals are Wiener integrals.
References
| [a1] | K. Itô, "Multiple Wiener integral" J. Math. Soc. Japan , 3 (1951) pp. 157–169 |
| [a2] | G. Kallianpur, "Stochastic filtering theory" , Springer (1980) |
| [a3] | H.-H. Kuo, "Gaussian measures in Banach spaces" , Lecture Notes in Mathematics , 463 , Springer (1975) |
| [a4] | H.-H. Kuo, "White noise distribution theory" , CRC (1996) |
| [a5] | N. Obata, "White noise calculus and Fock space" , Lecture Notes in Mathematics , 1577 , Springer (1994) |
| [a6] | N. Wiener, "The homogeneous chaos" Amer. J. Math. , 60 (1938) pp. 897–936 |
Wiener-Itô decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wiener-It%C3%B4_decomposition&oldid=50614