Wall invariant
An element of the Wall group, representing the obstruction to the surgery of a bordism to a simple homotopy equivalence.
Let $ X $ be a finite Poincaré complex, $ \nu $ a fibre bundle over $ X $ and $ x = [( M, \phi , F )] \in \Omega ( X, \nu ) $ a bordism class, where $ m $ is the formal dimension of $ X $ and $ \phi : M \rightarrow X $ has degree 1. This mapping can always be represented by an $ [ m/2] $- connected mapping using a finite sequence of surgeries. Let $ \Lambda = Z [ \pi _ {1} ( X)] $ be a group ring and let $ \overline{ {}}\; $ be the involution on $ \Lambda $ given by the formula $ \overline{ {\sum _ {g} n ( g) g }}\; = \sum w ( g) n ( g) g ^ {-1} $, where $ w: \pi _ {1} ( X) \rightarrow \{ 1, - 1 \} $ is defined by the first Stiefel–Whitney class of $ \nu $. Put
$$ K ^ {*} ( M) = \ \mathop{\rm coker} ( \phi ^ {*} : H ^ {*} ( X) \rightarrow H ^ {*} ( M)), $$
$$ K _ {*} ( M) = \mathop{\rm ker} ( \phi _ {*} : H _ {*} ( M) \rightarrow H _ {*} ( X)) $$
(coefficients in $ \Lambda $). The involution is an anti-isomorphism and there is defined the Wall group $ U _ {n} ( \Lambda ) = L _ {n} ( \pi _ {1} ( X), w) $.
Suppose now that $ m = 2k \geq 4 $. Then in the stable free $ \Lambda $- module $ G = K _ {k} ( M) = \pi _ {k + 1 } ( \phi ) $ one can choose a basis, and Poincaré duality induces a simple isomorphism $ \lambda : G \rightarrow G ^ {*} = K ^ {k} ( M) $, where $ ( G, \lambda ) $ is a $ (- 1) ^ {k} $- form. One therefore obtains the class $ \Theta _ {2k} ( x) = [( G, \lambda )] \in L _ {2k} ( \pi _ {1} ( X), w) $.
Suppose next that $ m = 2k + 1 \geq 5 $. One can choose generators in $ \pi _ {k + 1 } ( \phi ) = K _ {k} ( M; \Lambda ) $ so that they represent the imbeddings $ f _ {i} : S ^ {k} \times D ^ {k + 1 } \rightarrow M $, with non-intersecting images, and these images are connected by paths with a base point. Put $ U = \cup _ {i} \mathop{\rm Im} f _ {i} $, $ M _ {0} = M \setminus \mathop{\rm Int} U $. Since $ \phi \circ f _ {i} \sim 0 $, one may replace $ \phi $ by a homotopy and suppose that $ \phi ( u) = * $. Because $ X $ is a Poincaré complex, one can replace $ X $ by a complex with a unique $ m $- cell, i.e. one has a Poincaré pair $ ( X _ {0} , S ^ {m + 1 } ) $ and $ X = X _ {0} \cup e ^ {m} $. By the choice of a suitable cellular approximation one obtains a mapping for the Poincaré triad of degree 1: $ \phi : ( M; M _ {0} , U) \rightarrow ( X; X _ {0} , e ^ {m} ) $. Consequently one has the diagram of exact sequences:
$$
Moreover, one has a non-degenerate pairing $ \lambda : K _ {k} ( \partial U) \times K _ {k} ( \partial U) \rightarrow \Lambda $, where $ H = ( K _ {k} ( \partial U), \lambda ) $ is a quadratic $ (- 1) ^ {k} $- form while $ K _ {k + 1 } ( U, \partial U) $ and $ K _ {k + 1 } ( M _ {0} , \partial U) $ define its Lagrange planes $ L $ and $ P $. Then $ \Theta _ {2k + 1 } ( x) = [( H; L, P)] \in U _ {2k + 1 } ( \Lambda ) = L _ {2k + 1 } ( \pi _ {1} ( x), w) $.
The elements $ \Theta _ {m} ( x) \in L _ {m} ( \pi _ {1} ( x), w) $ defined above are called the Wall invariants. An important property is the independence of $ \Theta ( x) $ on the choices in the construction and the equivalence of the equation $ \Theta ( x) = 0 $ to the representability of the class as a simple homotopy equivalence, cf. [1].
References
| [1] | C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970) |
| [2] | A.A. Ranicki, "The algebraic theory of surgery I" Proc. London Math. Soc. , 40 : 1 (1980) pp. 87–192 |
| [3] | S.P. Novikov, "Algebraic construction and properties of Hermitian analogs of 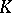 -theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes I" Math. USSR Izv. , 4 : 2 (1970) pp. 257–292 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 2 (1970) pp. 253–288 -theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes I" Math. USSR Izv. , 4 : 2 (1970) pp. 257–292 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 2 (1970) pp. 253–288 |
Wall invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wall_invariant&oldid=55144