User:Maximilian Janisch/latexlist/Algebraic Groups/Lie algebra, semi-simple
A Lie algebra that has no non-zero solvable ideals (see Lie algebra, solvable). Henceforth finite-dimensional semi-simple Lie algebras over a field $k$ of characteristic 0 are considered (for semi-simple Lie algebras over a field of non-zero characteristic see Lie algebra).
The fact that a finite-dimensional Lie algebra $8$ is semi-simple is equivalent to any of the following conditions:
1) $8$ does not contain non-zero Abelian ideals;
2) the Killing form of $8$ is non-singular (Cartan's criterion);
3) $8$ splits into the direct sum of non-Abelian simple ideals;
4) every finite-dimensional linear representation of $8$ is completely reducible (in other words: every finite-dimensional $8$-module is semi-simple);
5) the one-dimensional cohomology of $8$ with values in an arbitrary finite-dimensional $8$-module is trivial.
Any ideal and any quotient algebra of a semi-simple Lie algebra is also semi-simple. The decomposition of a semi-simple Lie algebra mentioned in condition 3) is unique. A special case of condition 5) is the following assertion: All derivations of a semi-simple Lie algebra are inner. The property of a Lie algebra of being semi-simple is preserved by both extensions and restrictions of the ground field.
Let $8$ be a semi-simple Lie algebra over an algebraically closed field $k$. The adjoint representation maps $8$ isomorphically onto the linear Lie algebra $g$, which is the Lie algebra of the algebraic group $g$ of all automorphisms of $8$ and is therefore an algebraic Lie algebra (cf. Lie algebra, algebraic). An element $X \in q$ is said to be semi-simple (nilpotent) if $\operatorname { ad } X$ is semi-simple (respectively, nilpotent). This property of an element $x$ is preserved by any homomorphism of $8$ into another semi-simple Lie algebra. The identity component $( \text { Aut } \mathfrak { g } ) ^ { 0 }$ coincides with the group of inner automorphisms of $8$, that is, it is generated by the automorphisms of the form $( \text { ad } X )$, $X \in q$.
In the study of semi-simple Lie algebras over an algebraically closed field $k$ an important role is played by the roots of a semi-simple Lie algebra, which are defined as follows. Let $h$ be a Cartan subalgebra of $8$. For a non-zero linear function $\alpha \in h ^ { * }$, let $\mathfrak { g } _ { Q }$ denote the linear subspace of $8$ given by the condition
\begin{equation} \mathfrak { g } _ { \alpha } = \{ X \in \mathfrak { g } : [ H , X ] = \alpha ( H ) X , H \in \mathfrak { h } \} \end{equation}
If $\mathfrak { g } _ { \alpha } \neq 0$, then $6$ is called a root of $8$ with respect to $h$. The set $2$ of all non-zero roots is called the root system, or system of roots, of $8$. One has the root decomposition
\begin{equation} \mathfrak { g } = \mathfrak { h } + \sum _ { \alpha \in \Sigma } \mathfrak { g } _ { \alpha } \end{equation}
The root system and the root decomposition of a semi-simple Lie algebra have the following properties:
a) $2$ generates $b ^ { x }$ and is a reduced root system in the abstract sense (in the linear hull of $2$ over the field of the real numbers). The system $2$ is irreducible if and only if $8$ is simple.
b) For any $\alpha \in \Sigma$,
\begin{equation} \mathfrak { g } _ { \alpha } = \operatorname { dim } [ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { - \alpha } ] = 1 \end{equation}
There is a unique element $H _ { \alpha } \in [ \mathfrak { g } _ { \alpha } , \mathfrak { g } - \alpha ]$ such that $\alpha ( H _ { \alpha } ) = 2$.
c) For every non-zero $X _ { \alpha } \in \mathfrak { g } _ { Q }$ there is a unique $Y _ { \alpha } \in \mathfrak { g } _ { - \alpha }$ such that $[ X _ { \alpha } , Y _ { \alpha } ] = H _ { \alpha }$, and
\begin{equation} [ H _ { \alpha } , X _ { \alpha } ] = 2 X _ { \alpha } \quad \text { and } \quad [ H _ { \alpha } , Y _ { \alpha } ] = - 2 Y _ { 0 } \end{equation}
Moreover,
\begin{equation} \beta ( H _ { \alpha } ) = \frac { 2 ( \alpha , \beta ) } { ( \alpha , \alpha ) } , \quad \alpha , \beta \in \Sigma \end{equation}
where $( , )$ is the scalar product induced by the Killing form.
d) If $\alpha , \beta \in \Sigma$ and $\alpha + \beta \neq 0$, then $\mathfrak { g } _ { Q }$ and $98$ are orthogonal with respect to the Killing form and $[ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { \beta } ] = \mathfrak { g } _ { \alpha + \beta }$.
A basis $\{ \alpha _ { 1 } , \dots , \alpha _ { n } \}$ of the root system $2$ is also called a system of simple roots of the algebra $8$. Let $\Sigma _ { + }$ be the system of positive roots with respect to the given basis and let $X - \alpha = Y _ { Q }$ $( \alpha \in \Sigma _ { + } )$. Then the elements
\begin{equation} H _ { \alpha _ { 1 } } , \ldots , H _ { \alpha _ { k } } , X _ { \alpha } \quad ( \alpha \in \Sigma ) \end{equation}
form a basis of $8$, called a Cartan basis. On the other hand, the elements
\begin{equation} X _ { \alpha _ { i } } , X _ { - \alpha _ { i } } \quad ( i = 1 , \ldots , n ) \end{equation}
form a system of generators of $8$, and the defining relations have the following form:
\begin{equation} [ [ X _ { \alpha _ { i } } , X _ { - } , _ { i } ] , X _ { \alpha _ { j } } ] = n ( i , j ) X _ { \alpha _ { j } } \end{equation}
\begin{equation} [ [ X _ { \alpha _ { i } } , X _ { - } \alpha _ { i } ] , X _ { - \alpha _ { j } } ] = - n ( i , j ) X _ { \alpha _ { j } } \end{equation}
\begin{equation} ( \text { ad } X _ { \alpha _ { i } } ) ^ { 1 - n ( i , j ) } X _ { \alpha _ { j } } = 0 \end{equation}
\begin{equation} ( \text { ad } X _ { - } \alpha _ { i } ) ^ { 1 - n ( i , j ) } X _ { - } \alpha _ { j } = 0 \end{equation}
Here $j = 1 , \ldots , n$ and
\begin{equation} n ( i , j ) = \alpha _ { j } ( H _ { i } ) = \frac { 2 ( \alpha _ { i } , \alpha _ { j } ) } { ( \alpha _ { j } , \alpha _ { j } ) } \end{equation}
Property d) implies that
\begin{equation} [ X _ { \alpha } , X _ { \beta } ] = \left\{ \begin{array} { l l } { N _ { \alpha , \beta } X _ { \alpha + \beta } } & { \text { if } \alpha + \beta \in \Sigma } \\ { 0 } & { \text { if } \alpha + \beta \notin \Sigma } \end{array} \right. \end{equation}
where $N _ { \alpha , \beta } \in k$. The elements $X _ { a }$ $( \alpha \in \Sigma _ { + } )$ can be chosen in such a way that
\begin{equation} N _ { \alpha , \beta } = - N _ { - \alpha , - \beta } \quad \text { and } \quad N _ { \alpha , \beta } = \pm ( p + 1 ) \end{equation}
where $D$ is the largest integer such that $\beta - p \alpha \in \Sigma$. The corresponding Cartan basis is called a Chevalley basis. The structure constants of $8$ in this basis are integers, which makes it possible to associate with $8$ Lie algebras and algebraic groups (see Chevalley group) over fields of arbitrary characteristic. If $k = C$, then the linear hull over $R$ of the vectors
\begin{equation} X _ { \alpha } - X _ { - \alpha } , \quad i ( X _ { \alpha } + X _ { - \alpha } ) \quad ( \alpha \in \Sigma _ { + } ) \end{equation}
is a compact real form of $8$.
A semi-simple Lie algebra is defined up to an isomorphism by its Cartan subalgebra and the corresponding root system. More precisely, if $91$ and $82$ are semi-simple Lie algebras over $k$, $b _ { 1 }$ and $52$ are their Cartan subalgebras and $\Sigma _ { 1 }$ and $\Sigma _ { 2 }$ are the corresponding root systems, then every isomorphism $\mathfrak { h } _ { 1 } \rightarrow \mathfrak { h } _ { 2 }$ that induces an isomorphism of the root systems $\Sigma _ { 1 }$ and $\Sigma _ { 2 }$ can be extended to an isomorphism $\mathfrak { g } _ { 1 } \rightarrow \mathfrak { g } 2$. On the other hand, any reduced root system can be realized as the root system of some semi-simple Lie algebra. Thus, the classification of semi-simple Lie algebras (respectively, simple non-Abelian Lie algebras) over an algebraically closed field $k$ essentially coincides with the classification of reduced root systems (respectively, irreducible reduced root systems).
Simple Lie algebras that correspond to root systems of types $4$–$\Omega$ are said to be classical and have the following form.
Type $A _ { n }$, $n \geq 1$. $g = s [ ( n + 1 , k )$, the algebra of linear transformations of the space $k ^ { n + 1 }$ with trace 0; $\operatorname { dim } \mathfrak { g } = n ( n + 2 )$.
Type $B _ { y }$, $n \geq 2$. $g = 50 ( 2 n + 1 , k )$, the algebra of linear transformations of the space $k ^ { 2 n + 1 }$ that are skew-symmetric with respect to a given non-singular symmetric bilinear form; $\operatorname { dim } \mathfrak { g } = n ( 2 n + 1 )$.
Type $C$, $n \geq 3$. $g = s p ( n , k )$, the algebra of linear transformations of the space $k ^ { 2 x }$ that are skew-symmetric with respect to a given non-singular skew-symmetric bilinear form; $\operatorname { dim } \mathfrak { g } = n ( 2 n + 1 )$.
Type $D _ { n }$, $n \geq 4$. $g = \operatorname { so } ( 2 n , k )$, the algebra of linear transformations of the space $k ^ { 2 x }$ that are skew-symmetric with respect to a given non-singular symmetric bilinear form; $\operatorname { dim } \mathfrak { g } = n ( 2 n - 1 )$.
The simple Lie algebras corresponding to the root systems of types $E _ { 0 }$, $E _ { 7 }$, $E _ { 8 }$, $F _ { 4 }$, $G$ are called special, or exceptional (see Lie algebra, exceptional).
The Cartan matrix of a semi-simple Lie algebra over an algebraically closed field also determines this algebra uniquely up to an isomorphism. The Cartan matrices of the simple Lie algebras have the following form:
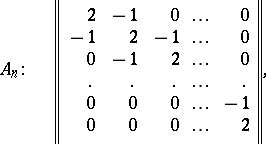 |
\begin{equation} \left\| \begin{array} { r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } \end{array} \right\| \end{equation}
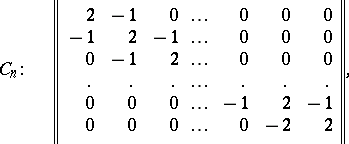 |
\begin{equation} \| \left. \begin{array} { r r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } & { - 1 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 2 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 0 } & { 2 } \end{array} \right. | \end{equation}
\begin{equation} \left\| \begin{array} { r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| \end{equation}
\begin{equation} \left\| \begin{array} { r r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| \end{equation}
\begin{equation} \left. \begin{array} { r l l l l l l l } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right. \end{equation}
\begin{equation} \left\| \begin{array} { r r r r } { 2 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 2 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| , \quad G _ { 2 } : \quad \left\| \begin{array} { r r } { 2 } & { - 1 } \\ { - 3 } & { 2 } \end{array} \right\| \end{equation}
The classification of split semi-simple Lie algebras over an arbitrary field $k$ of characteristic zero (a semi-simple Lie algebra $8$ is said to be split if it has a Cartan subalgebra $\mathfrak { h } \subset \mathfrak { g }$ such that all characteristic roots of the operators $\operatorname { ad } X$, $X \in \mathfrak { h }$, lie in $k$) goes in the same way as in the case of an algebraically closed field. Namely, to every irreducible reduced root system corresponds a unique split semi-simple Lie algebra. In particular, split semi-simple Lie algebras of types $4$–$\Omega$ have the form stated above, except that in the cases $B$ and $\Omega$ one must consider non-singular symmetric bilinear forms with Witt index $12$.
The problem of classifying arbitrary semi-simple Lie algebras over $k$ reduces to the following problem: To list, up to an isomorphism, all $k$-forms $90 \subset \mathfrak { g }$, that is, all $k$-subalgebras $90 \subset \mathfrak { g }$ such that $\mathfrak { g } = \mathfrak { g } 0 \otimes _ { k } K$. Here $K$ is an algebraically closed extension of $k$ and $8$ is a given semi-simple Lie algebra over $K$. The solution of this problem can also be obtained in terms of root systems (see Form of an algebraic group; Form of an (algebraic) structure). When $8$ is a classical simple Lie algebra over $k$ (other than $D _ { 4 }$), there is another method of classifying $k$-forms in $8$, based on an examination of simple associative algebras (see [3]).
When $k = R$ the classification of semi-simple Lie algebras goes as follows (see [6], [7]). Every simple non-Abelian Lie algebra over $R$ is either a simple Lie algebra over $m$ (regarded as an algebra over $R$), or the real form of a simple Lie algebra over $m$. The classification of real forms $80$ in a simple classical Lie algebra $8$ over $m$ is as follows:
I) Type $A _ { n }$: $g = s [ ( n + 1 , C )$, $n \geq 1$. $A _ { 1 }$: $go = s [ ( n + 1 , R )$. $A _ { I l }$: $t + 1 = 2 m$ is even, $90 = \operatorname { su } ^ { x } ( 2 n )$, the subalgebra of elements of $si ( 2 m , C )$ that preserve a certain quaternion structure. $A _ { U }$: $\mathfrak { g } 0 = \mathfrak { s u } ( p , n + 1 - p )$, the subalgebra of elements of $sl ( n + 1 , C )$ that are skew-symmetric with respect to a non-singular Hermitian form of positive index $D$, $0 \leq p \leq ( n + 1 ) / 2$
II) Type $B _ { y }$: $g = \operatorname { so } ( 2 n + 1 , C )$, $n \geq 2$. $B _ { 1 }$: $\mathfrak { g } 0 = \mathfrak { s o } ( p , 2 n + 1 - p )$, the algebra of a linear transformations of the space $R ^ { 2 x + 1 }$ that are skew-symmetric with respect to a non-singular symmetric bilinear form of positive index $D$, $0 \leq p \leq n$.
III) Type $C$: $\mathfrak { g } = \mathfrak { s p } ( n , C )$, $n \geq 3$. $C _ { 1 }$: $\mathfrak { g } 0 = \mathfrak { s p } ( n , R )$, the algebra of linear transformations of the space $R ^ { 2 x }$ that are skew-symmetric with respect to a non-singular skew-symmetric bilinear form. $C _ { I }$: $go = sp ( p , n - p )$, $0 \leq p \leq n / 2$, the subalgebra of $\operatorname { su } ( 2 p , 2 ( n - p ) )$ consisting of transformations that preserve a certain quaternion structure.
IV) Type $D _ { n }$: $g = \operatorname { so } ( 2 n , C )$, $n \geq 4$. $D _ { 1 }$: $\mathfrak { g } 0 = \mathfrak { s o } ( p , 2 n - p )$, the algebra of linear transformations of the space $R ^ { 2 x }$ that are skew-symmetric with respect to a non-singular bilinear symmetric form of positive index $D$, $0 \leq p \leq n$. $D _ { U }$: 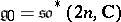 , the subalgebra of $\operatorname { so } ( 2 n , C )$ consisting of transformations that preserve a certain quaternion structure.
, the subalgebra of $\operatorname { so } ( 2 n , C )$ consisting of transformations that preserve a certain quaternion structure.
Semi-simple Lie algebras over the field $m$ were first considered in papers by W. Killing , who gave a classification of them, although in his proofs there were gaps, which were filled by E. Cartan [2]. In the papers of Killing and Cartan the roots of a Lie algebra appeared as the characteristic roots of the operator $\operatorname { ad } X$. Cartan also gave a classification of real semi-simple Lie algebras by establishing a deep connection between these algebras and globally symmetric Riemannian spaces (cf. Globally symmetric Riemannian space).
References
| [1a] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen I" Math. Ann. , 31 (1888) pp. 252–290 Zbl 20.0368.03 |
| [1b] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen II" Math. Ann. , 33 (1889) pp. 1–48 Zbl 20.0368.03 |
| [1c] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen III" Math. Ann. , 34 (1889) pp. 57–122 Zbl 21.0376.01 |
| [1d] | W. Killing, "Die Zusammensetzung der stetigen endlichen Transformationsgruppen IV" Math. Ann. , 36 (1890) pp. 161–189 MR1510618 |
| [2] | E. Cartan, "Sur la structure des groupes de transformations finis et continues" , Oeuvres complètes , 1 , Gauthier-Villars (1952) pp. 137–287 |
| [3] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) MR0148716 MR0143793 Zbl 0121.27504 Zbl 0109.26201 |
| [4] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [5] | R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1967) MR0476871 MR0466335 Zbl 0307.22001 Zbl 1196.22001 |
| [6] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) MR0514561 Zbl 0451.53038 |
| [7] | S. Araki, "On root systems and an infinitesimal classification of irreducible symmetric spaces" Osaka J. Math. , 13 (1962) pp. 1–34 MR0153782 Zbl 0123.03002 |
Comments
The defining relations, mentioned above, $( ad X _ { \alpha _ { i } } ) ^ { 1 - n ( i , j ) } ( X _ { \alpha _ { j } } ) = 0$, are known as the Serre relations.
It is customary to encode the information contained in the Cartan matrices $A _ { n }$–$G$ by means of the so-called Dynkin diagrams.'
|
The rules for recovering the Cartan matrix from the corresponding Dynkin diagram (also called Dynkin graph occasionally) are as follows. Number the vertices, e.g.,
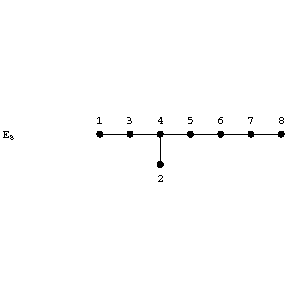
Figure: l058510a
On the diagonal of the Cartan matrix all elements are equal to 2. If nodes $i$ and $i$ are not directly linked, then the matrix entries $\alpha _ { j i } = \alpha _ { i j } = 0$. If two nodes $i$, $i$ are directly linked by a single edge, then $a _ { j } = - 1 = \alpha _ { j }$. If two nodes $i$, $i$ are directly linked by a double, respectively triple, edge and the arrow points from $i$ to $i$, then $a _ { j } = - 2$, $a _ { j i } = - 1$, respectively $a _ { j } = - 3$, $a _ { j i } = - 1$.
References
| [a1] | I.B. Frenkel, V.G. Kac, "Basic representations of affine Lie algebras and dual resonance models" Invent. Math. , 62 (1980) pp. 23–66 MR0595581 Zbl 0493.17010 |
| [a2] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) MR0682756 Zbl 0319.17002 |
| [a3] | J.-P. Serre, "Algèbres de Lie semi-simples complexes" , Benjamin (1966) MR0215886 Zbl 0144.02105 |
| [a4] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 MR0323842 Zbl 0254.17004 |
Maximilian Janisch/latexlist/Algebraic Groups/Lie algebra, semi-simple. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Lie_algebra,_semi-simple&oldid=44025