Universal behaviour in dynamical systems
In the late 1970's, P. Coullet and C. Tresser [a6] and M. Feigenbaum
independently found striking, unexpected features of the transition from simple to chaotic dynamics in one-dimensional dynamical systems (cf. also Routes to chaos). By the example of the family of quadratic mappings $ f _ \mu ( x)= 1- \mu x ^ {2} $ acting (for $ 0 \leq \mu \leq 2 $) on the interval $ x \in [- 1, 1] $, the period-doubling scenario is recalled here. For $ \mu = 2 $, $ f _ \mu $ has periodic points of every (least) period. Let $ \mu _ {i } $ be the infimum of parameter values $ \mu $ for which $ f _ \mu $ has a periodic orbit of least period $ 2 ^ {i } $. Then
$$ 0 < \mu _ {0} < \mu _ {1} < \dots , $$
and
$$ \sup \mu _ {i } = \mu _ \infty \sim 1.401155 \dots . $$
For $ \mu _ {i } < \mu \leq \mu _ {i+ 1 } $, the dynamics of $ f _ \mu $ is described by statements i)–iii) below.
i) $ f _ \mu $ has precisely one periodic orbit $ \Lambda _ {j} $ of (least) period $ 2 ^ {j} $ for each $ j= 0 \dots i $, and no other periodic orbits;
ii) any pair of adjacent points in $ \Lambda _ {i } $ is separated by a unique point in $ \cap _ {j< i } \Lambda _ {j} $;
iii) with the exception of the (countably many) orbits which land on some $ \Lambda _ {j} $, $ j< i $, and stay there, every $ f _ \mu $- orbit tends asymptotically to $ \Lambda _ {i } $.
For $ \mu = \mu _ \infty $( when $ f _ \mu $ is sometimes called the Feigenbaum mapping), statement i) holds, but with $ j $ ranging over all non-negative integers, and ii) holds for each $ i= 0, 1,\dots $; furthermore, the following analogue of iii) holds:
iv) (for $ \mu = \mu _ \infty $) the closure of the orbit of the turning point $ 0 $ is a Cantor set $ \Lambda _ \infty $, which is the asymptotic limit of every orbit not landing on one of the periodic orbits $ \Lambda _ {i } $, $ i= 0, 1,\dots $. The restricted mapping $ f _ \mu \mid _ {\Lambda _ \infty } $ is a minimal homeomorphism (the "adding machine for chaos in a dynamical systemadding machine" ).
Finally, $ \mu = \mu _ \infty $ is the threshold of "chaos" , in the following sense:
v) for $ \mu > \mu _ \infty $, $ f _ \mu $ has infinitely many distinct periodic orbits, and positive topological entropy.
Many features of this "topological" , or combinatorial picture were understood by early researchers in this area, specifically P.J. Myrberg [a12] and N. Metropolis, M.L. Stein and P.R. Stein [a13]. They recognized as well that the combinatorial structure of the periodic orbits $ \Lambda _ {j} $ is rigidly determined by the fact that $ f _ \mu $ is unimodal (cf. [a14]). In essence, the statements above can be formulated for any family of unimodal mappings (cf. ). In fact, the (weak) monotonicity of the $ \mu _ {i } $' s, together with the fact that if $ \mu < \mu _ \infty $, then $ f _ \mu $ must have periodic orbits of least period $ 2 ^ {j} $ for $ j= 0 \dots i $( some $ i $) and no others, follows for any family of continuous mappings on the line from Sharkovskii's theorem [a16], [a2]; recent work has yielded a more general understanding of the combinatorial structure of periodic orbits for continuous mappings in dimension $ 1 $( cf. [a1]).
Coullet, Tresser and Feigenbaum added to the topological picture described above a number of analytic and geometric features:
vi) the convergence $ \mu _ {i } \uparrow \mu _ \infty $ is asymptotically geometric:
$$ \lim\limits _ {i \rightarrow \infty } \ \frac{\mu _ \infty - \mu _ {i } }{\mu _ \infty - \mu _ {i+ 1 } } = \delta \sim 4.669 \dots ; $$
vii) the periodic orbits scale: let $ \Lambda _ {i } ^ {*} $ denote the orbit $ \Lambda _ {i } $ for $ \mu = \mu _ {i+ 1 } $; then
$$ \lim\limits _ {i \rightarrow \infty } \ \frac{ \mathop{\rm dist} ( 0, \Lambda _ {i } ^ {*} ) }{ \mathop{\rm dist} ( 0, \Lambda _ {i+ 1 } ^ {*} ) } = \alpha \sim \ 2.5029 \dots . $$
These statements, formulated for the particular family $ f _ \mu $ of quadratic mappings, are technically interesting, but not so striking. However, they observed that v)–vii) hold for a very broad class of unimodal one-parameter families, subject only to trivial "fullness" conditions (essentially that $ f _ {0} $ has only finitely many periodic orbits while $ f _ {2} $ has positive entropy) and smoothness (essentially that $ ( x, \mu ) \rightarrow f _ \mu ( x) $ is $ C ^ {2} $ and each $ f _ \mu $ has a non-degenerate critical point). And, sensationally, the constants $ \delta $ and $ \alpha $ are independent of the family $ f _ \mu $.
In [a6] and
these assertions were reduced, using ideas from renormalization theory, to certain technical conjectures concerning a doubling operator $ {\mathcal R} $ acting on an appropriate function space. O. Lanford
(cf. also [a3], [a5]) gave a rigorous, computer-assisted proof of the basic conjecture, that $ {\mathcal R} $ has a saddle-type fixed point with one characteristic multiplier $ \delta \sim 4.669 \dots $( the same as in vi)) and stable manifold of codimension $ 1 $. D. Sullivan [a17] showed the uniqueness of this fixed point in the space of "quadratic-like" mappings. The final conjecture, concerning transversality of the stable manifold with certain bifurcation submanifolds, remains unproved. Recently, Sullivan , introducing a number of new ideas, has circumvented this difficulty and provided a rather complete theory of universal features for families of $ C ^ {2} $ unimodal mappings. In particular, the asymptotic geometry of the Cantor set $ \Lambda _ \infty $( for $ \mu = \mu _ \infty $) and of analogous sets appearing at other "threshold" parameter values (the "infinitely renormalizable mappings of bounded type" ) is universal; for example, the set $ \Lambda _ \infty $ always has Hausdorff dimension $ 0.538045 $. Full expositions of this theory are provided in [a18] and [a7].
These ideas have been applied as well to circle diffeomorphisms [a10],
and area-preserving planar diffeomorphisms [a4], .
References
| [a1] | Ll. Alsedà, J. Llibre, M. Misiurewicz, "Combinatorial dynamics and entropy in one dimension" (to appear) |
| [a2] | L. Block, J. Guckenheimer, M. Misiurewicz, L.-S. Young, "Periodic points and topological entropy of one dimensional maps" Z. Nitecki (ed.) C. Robinson (ed.) , Global theory of dynamical systems (Proc. Northwestern Univ., 1979) , Lect. notes in math. , 819 , Springer (1980) pp. 18–34 MR0591173 Zbl 0447.58028 |
| [a3] | M. Campanino, H. Epstein, D. Ruelle, "On the existence of Feigenbaum's fixed point" Comm. Math. Phys. , 79 (1981) pp. 261–302 MR612250 |
| [a4] | P. Collet, J.-P. Eckmann, H. Koch, "On universality for area-preserving maps of the plane" Physica , 3D (1981) pp. 457–467 MR0631180 Zbl 1194.37050 |
| [a5] | P. Collet, J.-P. Eckmann, O. Lanford, "Universal properties of maps on an interval" Comm. Math. Phys. , 76 (1980) pp. 211–254 MR0588048 Zbl 0455.58024 |
| [a6] | P. Coullet, C. Tresser, "Itérations d'endomorphismes et groupe de rénormalisation" J. Phys. , C5 (1978) pp. 25–28 MR0512110 |
| [a7] | W. de Mello, S. van Strien, "One-dimensional dynamics" (to appear) |
| [a8a] | M. Feigenbaum, "Quantitative universality for a class of non-linear transformations" J. Stat. Phys. , 19 (1978) pp. 25–52 MR501179 |
| [a8b] | M. Feigenbaum, "The universal metric properties of a non-linear transformation" J. Stat. Phys. , 21 (1979) pp. 669–706 MR555919 |
| [a9a] | L. Jonker, D. Rand, "Bifurcations in one dimension" Invent. Math. , 62 (1981) pp. 347–365 MR0608525 MR0604832 Zbl 0475.58015 |
| [a9b] | L. Jonker, D. Rand, "Bifurcations in one dimension" Invent. Math. , 63 (1981) pp. 1–16 MR0608525 MR0604832 Zbl 0475.58015 |
| [a10] | L. Jonker, D. Rand, "Universal properties of maps of the circle with  -singularities" Comm. Math. Phys. , 90 (1983) pp. 273–292 MR714439 -singularities" Comm. Math. Phys. , 90 (1983) pp. 273–292 MR714439 |
| [a11a] | O. Lanford, "A computer-assisted proof of the Feigenbaum conjectures" Bull. Amer. Math. Soc. , 6 (1982) pp. 427–434 MR0648529 Zbl 0487.58017 |
| [a11b] | O.E. Lanford, "Computer assisted proofs in analysis" A.M. Gleason (ed.) , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 1385–1394 MR0934342 Zbl 0676.65039 |
| [a12] | P.J. Myrberg, "Sur l'iteration des polynomes réels quadratiques" J. Math. Pures Appl. , 41 (1962) pp. 339–351 MR0161968 Zbl 0106.04703 |
| [a13] | N. Metropolis, M.L. Stein, P.R. Stein, "On finite limit sets for transformations on the unit interval" J. Comb. Theory , 15A (1973) pp. 25–44 MR0316636 Zbl 0259.26003 |
| [a14] | W. Thurston, "On iterated maps of the interval" J.C. Alexander (ed.) , Dynamical Systems (Proc. Maryland, 1986–7) , Lect. notes in math. , 1342 , Springer (1988) pp. 465–563 MR0970571 Zbl 0664.58015 |
| [a15a] | D. Rand, "Universality and renormalization in dynamical systems" T. Bedford (ed.) J. W. Swift (ed.) , New directions in dynamical systems , Cambridge Univ. Press (1987) pp. 1–56 |
| [a15b] | D. Rand, "Global phase space universality, smooth conjugacies and renormalisation: the 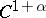 case." Nonlinearity , 1 (1988) pp. 181–202 MR928952 case." Nonlinearity , 1 (1988) pp. 181–202 MR928952 |
| [a16] | A.N. Sharkovskii, "Coexistence of cycles of a continuous map of the line into itself" Ukrain. Mat. Zh. , 16 (1964) pp. 61–71 (In Russian) MR1415876 MR1361914 |
| [a17] | D. Sullivan, "Quasiconformal homeomorphisms in dynamics, topology and geometry" A.M. Gleason (ed.) , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 1216–1228 MR0934326 Zbl 0698.58030 |
| [a18] | D. Sullivan, "Bounds, quadratic differentials, and renormalization conjectures" , Centennial Publ. , 2 , Amer. Math. Soc. (1991) MR1184622 Zbl 0936.37016 |
Universal behaviour in dynamical systems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universal_behaviour_in_dynamical_systems&oldid=49089