Thom spectrum
A spectrum of spaces, equivalent to the spectrum associated to a certain structure series (cf. $ ( B, \phi ) $-
structure).
Let $ ( B _ {n} , \phi _ {n} , g _ {n} ) $ be a structure series, and let $ \xi _ {n} $ be the bundle over $ B _ {n} $ induced by the mapping $ \phi _ {n} : B _ {n} \rightarrow \mathop{\rm BO} _ {n} $. Let $ T _ {n} $ be the Thom space of $ \xi _ {n} $. The mapping $ g _ {n} $ induces a mapping $ S _ {n} : ST _ {n} \rightarrow T _ {n + 1 } $, where $ S $ is suspension and $ ST \xi _ {n} = T( \xi _ {n} \oplus \theta ) $( $ \theta $ is the one-dimensional trivial bundle). One obtains a spectrum of spaces $ \{ T \xi _ {n} \} = T ( B, \phi , g) $, associated with the structure series $ ( B _ {n} , \phi _ {n} , g _ {n} ) $, and a Thom spectrum is any spectrum that is (homotopy) equivalent to a spectrum of the form $ T ( B, \phi , g) $. It represents $ ( B, \phi ) $- cobordism theory. Thus, the series of classical Lie groups $ O _ {k} $, $ \mathop{\rm SO} _ {k} $, $ U _ {k} $, and $ \mathop{\rm Sp} _ {k} $ lead to the Thom spectra $ \mathop{\rm TBO} $, $ \mathop{\rm TBSO} $, $ \mathop{\rm TBU} $, and $ \mathop{\rm TBSp} $.
Let $ \beta _ {n} $ be Artin's braid group on $ n $ strings (cf. Braid theory). The homomorphism $ \beta _ {n} \rightarrow S _ {n} \subset O _ {n} $, where $ S _ {n} $ is the symmetric group, yields a mapping $ B \beta _ {n} \rightarrow \mathop{\rm BO} _ {n} $ such that a structure series arises ( $ \beta _ {n} $ is canonically imbedded in $ \beta _ {n + 1 } $). The corresponding Thom spectrum is equivalent to the Eilenberg–MacLane spectrum $ K ( \mathbf Z /2) = \{ K ( \mathbf Z /2, n) \} $, so that $ K ( \mathbf Z /2) $ is a Thom spectrum (cf. [1], [2]). Analogously, $ K ( \mathbf Z ) $ is a Thom spectrum, but using sphere bundles, [3].
References
| [1] | M. Mahowold, "A new infinite family in 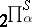 " Topology , 16 (1977) pp. 249–256 " Topology , 16 (1977) pp. 249–256 |
| [2] | S. Priddy, " as a Thom spectrum" Proc. Amer. Math. Soc. , 70 : 2 (1978) pp. 207–208 as a Thom spectrum" Proc. Amer. Math. Soc. , 70 : 2 (1978) pp. 207–208 |
| [3] | M. Mahowold, "Ring spectra which are Thom complexes" Duke Math. J. , 46 : 3 (1979) pp. 549–559 |
Thom spectrum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thom_spectrum&oldid=48972