Tangent, curve of the
The graph of the function $g=\tan x$ (Fig.a). The curve of the tangent is a periodic curve with period $T=\pi$ and asymptotes $x=(k+1/2)\pi$, $k\in\mathbf Z$. While $x$ varies from $-\pi/2$ to $+\pi/2$, $y$ grows monotonically from $-\infty$ to $+\infty$; thus, the curve of the tangent is composed of infinitely many separate congruent curves obtained from one another by translation over $k\pi$ along the $x$-axis. The points of intersection with the $x$-axis are $(k\pi,0)$. These are also the points of inflection, with inclination angle $\pi/4$ to the $x$-axis.
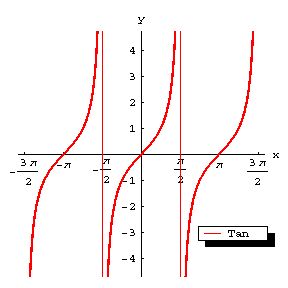
Figure: t092130a
The curve of the tangent reflected mirror-like in the $x$-axis and translated to the left over $\pi/2$ (Fig.b) becomes the graph of the function $y=\operatorname{cotan}x=-\tan(\pi/2+x)$ (cf. Cotangent); its asymptotes are $x=k\pi$; its intersections with the $x$-axis are $((k+1/2)\pi,0)$ and these points are also the points of inflection, with inclination angle $\pi/4$ with respect to the $x$-axis.
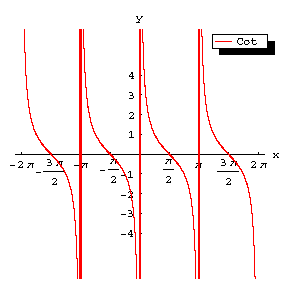
Figure: t092130b
Tangent, curve of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent,_curve_of_the&oldid=33317