Talk:Elementary matrix
Issue
This definition excludes the row-switching elementary matrix[1]:
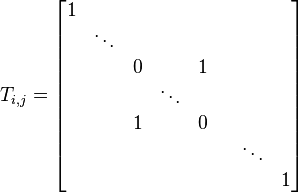
Proof
The matrix above (marked T) has more than one off-diagonal element added to it.
In addition, at least one diagonal element has been modified.
Therefore, by the definition on the Elementary matrix page, T is not an elementary matrix.
Alternative definition (example)
Wikipedia defines elementary matrix in the following manner:
In mathematics, an elementary matrix is a matrix which differs from the identity matrix by one single elementary row operation.[2]
Although this definition requires elementary row operations to be defined, the matrix that matches the Row-switch operation is "elementary", by this definition.
References
--Ben Paradise (talk) 14:24, 20 March 2015 (CET)
Comments
- Thank you. Probably you are right. But, being not an algebraist, I am not sure: maybe different (non-equivalent) definitions are in use? Boris Tsirelson (talk) 19:13, 20 March 2015 (CET)
- Thanks for the reply! I also noticed that the same issue exists for Row-multiplying transformations.
- Theorems regarding the connection between elementary row operations and elementary matrices are based on this definition.
- Pending review by an Algebraist. --Ben Paradise (talk) 19:49, 20 March 2015 (CET)
- In fact, there are different traditions. Introductory linear algebra textbooks tend to use the definition of elementary matrices as given in WP, in particular in the context of "elementary row and column transformations". In [1, p. 131] three types are given, which could be represented as follows:
$$ \text{Type I:} \quad \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \qquad \text{Type II:} \quad\begin{pmatrix} 1 & 0 \\ 0 & a \end{pmatrix},\ a\ne 0, \qquad \text{Type III:}\quad\begin{pmatrix} 1 & a \\ 0 & 1 \end{pmatrix} $$
- In books related to group theory [2, p. 23] or K-theory [3, p. 25], the definition as given here in EoM is used (just Type III).
- One significant difference is that matrices of Type I, II have determinant $\ne 1$, while those of Type III always have determinant $1$. All these matrices generate the "General Linear Group", while Type III matrices generate what is called the "Elementary Group", which, over fields, is the group of all matrices with determinant $1$.
- In [4, p. 363], elementary matrices are defined to be just those of Type II and III, which also makes sense, since Type I can be obtained as a product of Type II, III (hence the former isn't quite as "elementary"):
$$ \begin{pmatrix} 1 & a \\ 0 & 1\end{pmatrix} \begin{pmatrix} 1 & 0 \\ -a & 1\end{pmatrix} \begin{pmatrix} 1 & a \\ 0 & 1\end{pmatrix} \begin{pmatrix}-a & 0 \\ 0 & 1\end{pmatrix} = \begin{pmatrix} 0 & a \\ -a^{-1} & 0\end{pmatrix} \begin{pmatrix}-a & 0 \\ 0 & 1\end{pmatrix} = \begin{pmatrix} 0 & a \\ 1 & 0\end{pmatrix}. $$
- May be we should augment our definition by saying that the definition depends on the respective author (and context).
- In fact the situation is a bit confusing, even WP is not quite consistent: On their page [1] it is said at one place that the elementary group $E(A)$ is the group of "elementary matrices", which of course is not so according to their definitions.
- [1] Meyer, Carl D, Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), (2004) ISBN 978-0-89871-454-8
- [2] A.J. Hahn, O.T. O'Meara The classical groups and K-Theory, Grundlehren, Springer (1989)
- [3] J. Milnor, Introduction to algebraic K-theory, Annals of Math Studies 71, Princeton University Press (1971)
- [4] A.G. Kurosh, "Higher algebra", MIR (1972) (Translated from Russian)
- --Ulf Rehmann (talk) 01:03, 26 March 2015 (CET)
- I see. Yes, it would be nice to mention this in the article. In fact, I did so in Measurable space#On terminology and Measure space#On terminology. Is there a better place for such clarifications than an encyclopedia? Boris Tsirelson (talk) 08:05, 26 March 2015 (CET)
- Yes, I will do so, after checking where in EoM the terms "elementary matrix|matrices" are used. E.g., the page Equivalent matrices distinguishes carefully and explicitly between permutation matrices, elementary matrices (in our sense), and diagonal matrices. The other EoM pages linking to this page describe content for which our definition is the adequate one (and the other would be misleading). --Ulf Rehmann (talk) 10:19, 26 March 2015 (CET)
- I see. Yes, it would be nice to mention this in the article. In fact, I did so in Measurable space#On terminology and Measure space#On terminology. Is there a better place for such clarifications than an encyclopedia? Boris Tsirelson (talk) 08:05, 26 March 2015 (CET)
Elementary matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_matrix&oldid=36365