System of parameters of a module over a local ring
Let $( A , \mathfrak m )$ be an $r$-dimensional Noetherian ring (cf. also the section "Dimension of an associative algebra" in Dimension). Then there exists an $\mathfrak{m}$-primary ideal generated by $r$ elements (cf., e.g., [a1], p. 98, [a2], p. 27). If $x _ { 1 } , \dots , x _ { r }$ generate such an $\mathfrak{m}$-primary ideal, they are said to be a system of parameters of $A$. The terminology comes from the situation that $( A , \mathfrak m )$ is the local ring of functions at a (singular) point on an algebraic variety. The system of parameters $x _ { 1 } , \dots , x _ { r }$ is a regular system of parameters if $x _ { 1 } , \dots , x _ { r }$ generate $\mathfrak{m}$, and in that case $( A , \mathfrak m )$ is a regular local ring.
More generally, if $M$ is a finitely-generated $A$-module of dimension $s$, then there are $y _ { 1 } , \dots , y _ { s } \in \mathfrak { m }$ such that $M / ( y _ { 1 } , \ldots , y _ { s } ) M$ is of finite length; in that case $y _ { 1 } , \dots , y _ { s }$ is called a system of parameters of $M$.
The ideal $( y _ { 1 } , \dots , y _ { s } )$ is called a parameter ideal.
For a semi-local ring $A$ with maximal ideals $m _ { 1 } , \dots , m _ { r }$, an ideal $\frak a$ is called an ideal of definition if
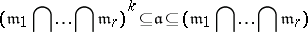 |
for some natural number $k$. If $A$ is of dimension $d$, then any set of $d$ elements that generates an ideal of definition is a system of parameters of $A$, [a3], Sect. 4.9.
References
| [a1] | H. Matsumura, "Commutative ring theory" , Cambridge Univ. Press (1989) |
| [a2] | M. Nagata, "Local rings" , Interscience (1962) |
| [a3] | D.G. Nothcott, "Lessons on rings, modules, and multiplicities" , Cambridge Univ. Press (1968) |
System of parameters of a module over a local ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=System_of_parameters_of_a_module_over_a_local_ring&oldid=50755