Symmetry
An involutory orthogonal transformation that changes the orientation (an involutory transformation is a transformation that, when applied twice, yields the identity). For example, a reflection with respect to a plane $ \alpha $
in space (or with respect to a straight line $ a $
in a plane) is a symmetry under which every point $ M $
is mapped to a point $ M ^ \prime $
such that the segment $ MM ^ \prime $
is perpendicular to the plane $ \alpha $(
the line $ a $)
and is bisected by it. $ \alpha $(
$ a $)
is called the plane (axis) of the symmetry (see ). Any orthogonal transformation, or isometry, is the composite of a finite number of reflections.
Symmetry is the following property of a geometrical figure $ \Phi $: $ \Phi $ is mapped onto itself under the action of some group $ G $ of transformations, called the group of symmetries of $ \Phi $. Thus, symmetry reflects a certain regularity of the shape of a figure, namely, its invariance under the action of transformations in $ G $. If, for example, $ \Phi $ is a plane figure such that rotation about some point $ O $ through an angle of $ 360 \circ /n $, where $ n $ is an integer, maps it onto itself, then $ \Phi $ possesses a symmetry of order $ n $, and $ O $ is called the centre of the symmetry (see Fig. b). Here $ G $ is the cyclic group of order $ n $. A circle has symmetry of infinite order (since it is mapped onto itself by a rotation through any angle).
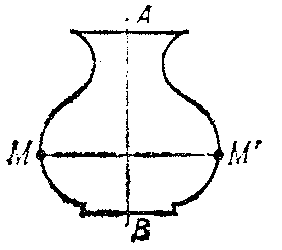
Figure: s091760a
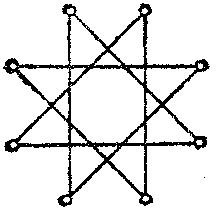
Figure: s091760b
Other simple forms of spatial symmetry are as follows.
a) A symmetry of order $ n $ about a straight line. Here the figure is mapped onto itself by a rotation about some straight line (the axis of symmetry) through an angle of $ 360 \circ /n $. For example, if a plane figure is symmetric with respect to a straight line $ AB $, then in space it has this straight line as an axis of symmetry of order 2. A cube has the line $ AB $ as an axis of symmetry of order 3, and the line $ CD $ as an axis of symmetry of order 4 (see Fig. c). In general, regular and semi-regular polyhedra are symmetric about several lines (see Fig. d). The position, number and orders of axes of symmetry play a fundamental role in crystallography.
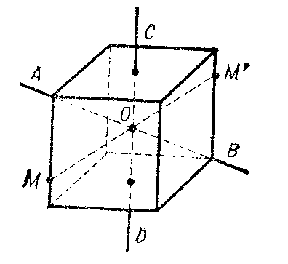
Figure: s091760c
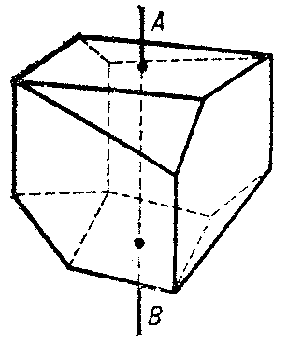
Figure: s091760d
b) Translational symmetry. Here a figure is mapped onto itself by translation along a certain straight line (the axis of the translation) over some interval. A figure with a unique axis of translation and one plane of symmetry may have infinitely-many planes of symmetry (since any translation is a composite of two reflections) perpendicular to the axis of translation (see Fig. e). Figures having several axes of translation play an important role in the study of crystalline lattices.

Figure: s091760e
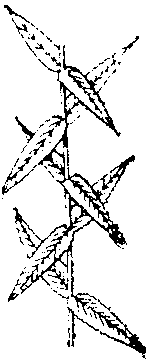
Figure: s091760f
Symmetries composed of reflections and rotations (which exhaust the simple symmetries of bounded figures) and also of translations are of interest and are a topic of study in various fields of the natural sciences, art, etc. For example, a twist or helical symmetry, composed of rotation through some angle about an axis and translation along that axis, is observed in the arrangement of leaves in plants (see Fig. f). Symmetry is widely propagated as one of the ways of constructing embroideries and ornaments (planar figures possessing one or several translational symmetries in combination with reflections, see Fig. g, Fig. h).

Figure: s091760g

Figure: s091760h
References
| [1] | A.V. Shubnikov, V.A. Koptsik, "Symmetry: in science and art" , Plenum (1974) (Translated from Russian) |
| [2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1959) |
| [3] | H. Weyl, "Symmetry" , Princeton Univ. Press (1952) (Translated from German) |
Comments
Quite generally, let $ G $ be a group acting on a set $ X $( e.g., $ G $ can be the group of Euclidean motions of $ \mathbf R ^ {n} $ and $ X $ can be some set of geometrical figures in $ \mathbf R ^ {n} $ closed under Euclidean motions). For each $ x \in X $ the isotropy subgroup $ G _ {x} = \{ g \in G : gx= x \} $ is the symmetry group of $ x $.
The statement that translational symmetry with a unique axis of translation implies symmetry with respect to planes is not correct in general.
References
| [a1] | D. Schattschneider, "Visions of symmetry" , Freeman (1990) |
| [a2] | B. Grünbaum, G.C. Shephard, "Tilings and patterns" , Freeman (1986) |
| [a3] | H.S.M. Coxeter, "Regular polytopes" , Macmillan (1963) |
Symmetry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetry&oldid=48930