Surface of the second order
A set of points in the three-dimensional real or complex space whose coordinates in a Cartesian coordinate system satisfy an algebraic equation of degree two:
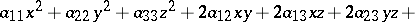 | (*) |
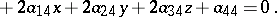 |
Equation (*) need not define a real geometric image, and in such cases one says that (*) defines an imaginary second-order surface. Depending on the coefficients in the general equation (*), one may transform it by parallel translation and rotation in the coordinate system to one of the 17 canonical forms given below, each of which corresponds to a certain class of surfaces. Precisely, the non-singular irreducible surfaces:
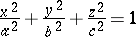 (an ellipsoid),
(an ellipsoid),
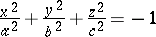 (an imaginary ellipsoid),
(an imaginary ellipsoid),
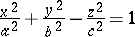 (a one-sheet hyperboloid),
(a one-sheet hyperboloid),
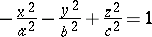 (a two-sheet hyperboloid),
(a two-sheet hyperboloid),
 ,
, 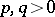 (an elliptic paraboloid),
(an elliptic paraboloid),
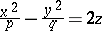 ,
, 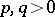 (a hyperbolic paraboloid);
(a hyperbolic paraboloid);
the singular irreducible surfaces: the cylindrical surfaces (cf. Cylindrical surface (cylinder)) —
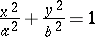 (an elliptic cylinder),
(an elliptic cylinder),
 (an imaginary elliptic cylinder),
(an imaginary elliptic cylinder),
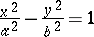 (a hyperbolic cylinder),
(a hyperbolic cylinder),
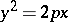 (a parabolic cylinder);
(a parabolic cylinder);
the conical surfaces (cf. Conical surface) —
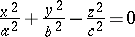 (a conical surface),
(a conical surface),
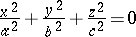 (an imaginary conical surface);
(an imaginary conical surface);
the singular reducible surfaces:
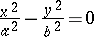 (a pair of intersecting planes),
(a pair of intersecting planes),
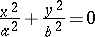 (a pair of imaginary intersecting planes),
(a pair of imaginary intersecting planes),
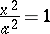 (a pair of parallel planes),
(a pair of parallel planes),
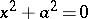 (a pair of imaginary parallel planes),
(a pair of imaginary parallel planes),
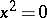 (a pair of coincident planes).
(a pair of coincident planes).
A second-order surface having a unique centre of symmetry (the centre of the surface) is called a central surface. The coordinates of the centre are defined as the solution to the system
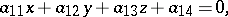 |
 |
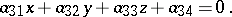 |
A second-order surface without a centre of symmetry or with an indeterminate centre is called a non-central surface.
One can examine second-order surfaces without reducing the general equation to a canonical form by the joint consideration of the so-called basic invariants of second-order surfaces. These are expressions made up from the coefficients of (*) whose values do not alter under parallel translation and rotation of the coordinate system:
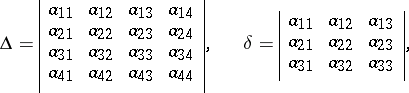 |
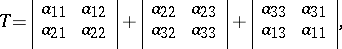 |
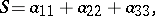 |
together with the semi-invariants 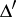 and
and 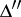 , which are invariant under rotation of the coordinate system:
, which are invariant under rotation of the coordinate system:
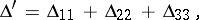 |
where 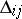 is the algebraic complement of
is the algebraic complement of 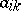 in
in 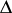 , and
, and
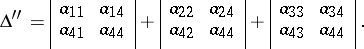 |
'
<tbody> </tbody>
|
The invariants, in general, define a second-order surface up to a motion in Euclidean space; if corresponding invariants for two surfaces are equal, these surfaces may be brought to coincide by a motion. In other words, these surfaces are equivalent in relation to the group of spatial motions (are metrically equivalent).'
<tbody> </tbody>
|
There is a classification of second-order surfaces from the point of view of other transformation groups. For example, with respect to the group of affine transformations, equivalence applies for any two surfaces defined by equations of the same canonical form, e.g. two similar second-order surfaces are equivalent.
The relationships between the various affine classes of second-order surfaces enable one to establish a classification from the point of view of projective geometry. Here one takes as equivalent those surfaces that can be mapped onto another by means of projective transformations. For example, ellipsoids, elliptic paraboloids and two-sheet hyperboloids are real oval surfaces from the point of view of projective geometry. Their projective equivalence manifests itself in that there is a certain system of projective coordinates in which the equations for these surfaces are identical in form:
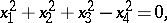 |
i.e. the corresponding quadratic forms 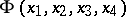 have identical rank
have identical rank
and identical signature . Their affine difference appears in the type of the line of intersection with the improper plane: an ellipsoid intersects it in an imaginary oval, a hyperboloid in a real oval and an elliptic paraboloid in a pair of imaginary intersecting straight lines. In all, there are eight projective equivalence classes for second-order surfaces:
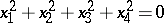 (an imaginary oval surface),
(an imaginary oval surface),
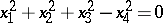 (a real oval surface),
(a real oval surface),
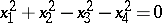 (an annular surface),
(an annular surface),
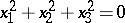 (an imaginary conical surface),
(an imaginary conical surface),
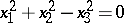 (a real conical surface),
(a real conical surface),
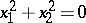 (a pair of imaginary planes),
(a pair of imaginary planes),
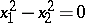 (a pair of real planes),
(a pair of real planes),
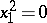 (a pair of coincident planes).
(a pair of coincident planes).
For references see Second-order curve.
Comments
Similar classifications are possible over other fields, such as 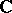 , finite fields and
, finite fields and 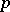 -adic fields.
-adic fields.
References
| [a1] | M. Berger, "Geometry" , II , Springer (1987) MR0903026 MR0895392 MR0882916 MR0882541 Zbl 0619.53001 Zbl 0606.51001 Zbl 0606.00020 |
| [a2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) MR0046650 Zbl 0047.38806 |
| [a3] | R.W. Brink, "Analytic geometry" , Appleton-Century (1935) MR1523468 Zbl 61.1393.02 |
| [a4] | A.V. Pogorelov, "Geometry" , Moscow (1987) (In Russian) MR1440529 MR0804808 MR0760631 MR0467543 MR0346714 MR0268787 MR0244909 MR0239488 MR1534647 MR0203551 MR0203550 MR1530777 MR0121692 MR0114163 MR0097836 Zbl 0907.51005 Zbl 0606.53003 Zbl 0521.53001 Zbl 0391.53001 Zbl 0311.53067 Zbl 0172.46401 Zbl 0141.36702 Zbl 0084.17702 |
| [a5] | A.V. Pogorelov, "Analytical geometry" , Moscow (1980) (In Russian) |
Surface of the second order. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Surface_of_the_second_order&oldid=24131
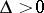
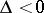
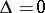
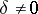
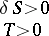
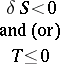
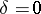
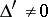
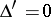
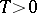
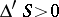 )
)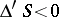 )
)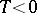
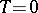
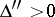 )
)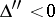 )
)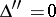 )
)