Sprouts
2020 Mathematics Subject Classification: Primary: 91A05 [MSN][ZBL]
Rules
Sprouts is a 2-person paper-and-pencil game created by J.H.Conway and M.S.Paterson in 1967 [G1]. It starts with $n$ points on a sheet of paper. The two players alternate with making moves. Each move consists of drawing a line between two points $a$ and $b$ ($a=b$ is a valid choice) and of adding a new point anywhere on the new line with exception of the endpoints. Planarity of the graph must be maintained, i.e. the line must not intersect another line or itself or cross one of the points already existing. The number of lines incident to a point is limited by three, whereby drawing a line from a point $p$ to itself is counted as two lines ending at $p$. In the normal version of Sprouts, the player making the last valid move wins; in the misère version, the player making the last valid move loses.

|
|
|
|
|
|
|
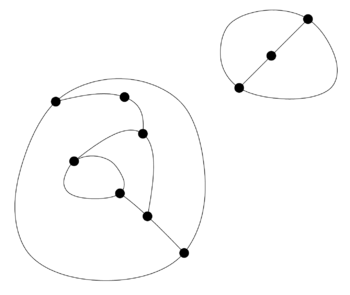
|
|
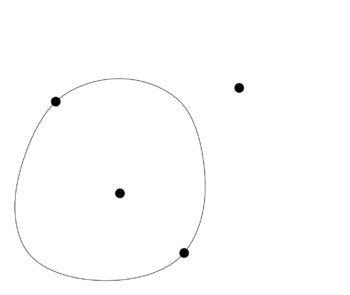
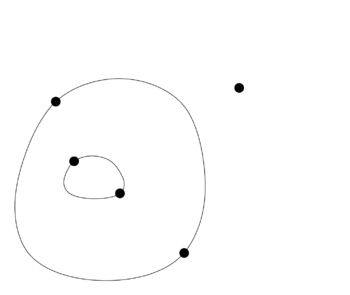
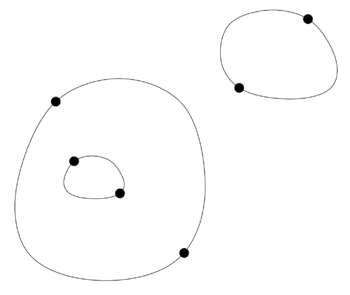
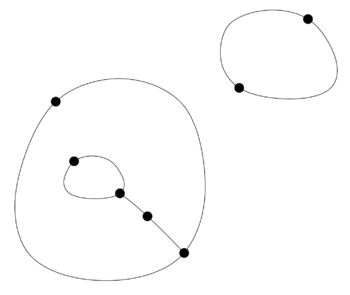
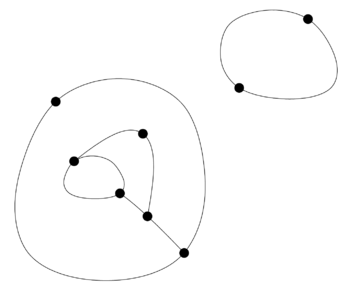
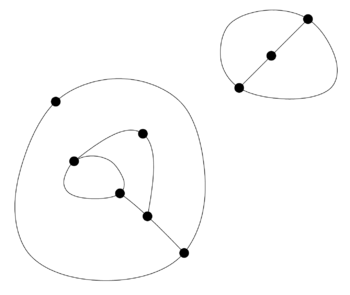
Example: Game of Sprouts starting with 3 points (with the second player as winner in the normal version). | |
Formal Representation
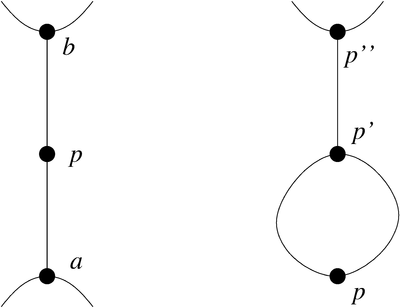
A Sprouts position can be formalized quite naturally as topological graph $\bar G=(\bar V,\bar E)$ embedded in the plane ${{\mathbb{R}}}^2$. The starting position of an $n$-points game is a planar graph $\bar G_0=(\bar V_0,\bar E_0)$ with $\bar V_0=\{p_1,\ldots,p_n\}$ and $\bar E=\emptyset$. A move in a position $\bar G_i=(\bar V_i,\bar E_i)$ consists of connecting two points $a,b\in \bar V$ with a line and placing a point $q$ on this line. The new line has to preserve planarity and consists of two edges $e_1,e_2$ (modelled as Jordan curves) with endpoints $a,q$ and $q,b$, respectively. The execution of this move gives a new graph [FL1] $\bar G_{i+1}=(\bar V_{i+1},\bar E_{i+1})$ with $\bar V_{i+1}:=\bar V_i\cup \{q\}$ and with $\bar E_{i+1}:= \bar E_i\cup \{e_1,e_2\}$.
The representation as topological graph is far too detailed, if only the outcome of a game is of interest. One possible option to abstract from irrelevant information --- like the precise shape of the edges --- is to consider equivalence classes of Sprouts positions with respect to homeomorphisms, because the gaming aspects of Sprouts positions --- (non)existence of valid moves --- are invariant under homeomorphisms [DHKR]: For two positions $A, B$ being homeomorphic to each other, all moves executed in the position $A$ can be transferred to the position $B$ and vice versa.
The elements of an equivalence class can be characterized at a purely combinatorical level by describing their node-, edge-, and face-structure. Such a description may consist of
- A set $V$ of nodes.
- A set $E$ of edges.
- A set $F$ of faces.
- A set $O$ giving for each node $v\in V$ the order of edges incident to $v$
- A set $B$ giving for each face $f\in F$ the subsets of nodes and edges contained in its boundary.
Equivalent descriptions are known and used in programs analyzing Sprouts.
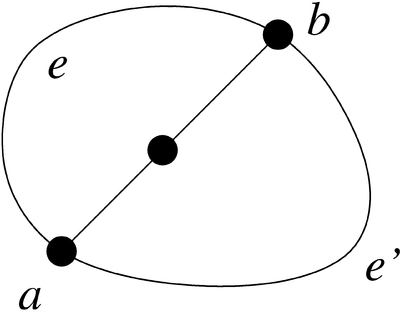
|
| The representation of edges by their endpoints only will not suffice, because there may be more than one edge in a Sprouts position with the same endpoints. |
Length of a Sprouts game
Maximum length of a game
A node is said to have $k$ lives, $k\le 3$, if its degree is $3-k$ [Pr]. A node is called dead, if it has no lives left. Otherwise, it is called alive. In a final position [L], nodes still alive have only one life; otherwise it would be possible to make another move (draw a line connecting this point with itself). A new point introduced in a move has already two lines incident to it and thus only one life remaining.
A Sprouts game starting with $n$ points has a total number of $3n$ lives at the beginning. Each move reduces the total number of lives in the position by 1, since the connecting line uses up two lives, whereas the new node adds one life. If only 1 life remaines, a valid move is not possible anymore. Thus a Sprouts game with $n$ initial points can not have more than $3n-1$ moves [C].
Minimum length of a game
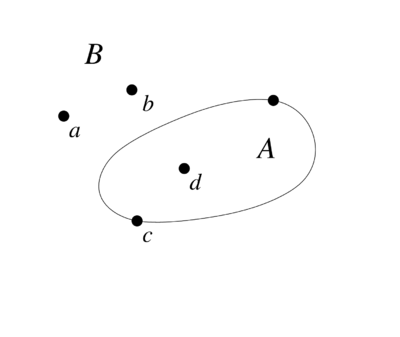
Two nodes of a topological graph are called topological neighbors, if they can be connected with an edge preserving planarity. In a final position, the topological neighbors of a node $p$ still alive are dead. Otherwise it would be possible to make another move according to the rules of the game. For $p$ at least two (dead) topological neighbours must exist [L].
If a game starts with $n$ nodes and ends after $m$ moves, the final position consists of exactly $n+m$ nodes. This node set consists of $s$ nodes still alive, $s'$ dead nodes being topological neighbors of nodes still alive and $s''$ dead nodes, which are no topological neighbor of a node still alive. This leads to the equation $n+m=s+s'+s''$. Since each of the $s$ points has exactly one life, it holds $s=3n-m$. Furthermore, the inequalities $s'\ge 2s= 2(3n-m)$ and $s''\ge 0$ will hold. This leads to $n+m \ge 3n-m+6n-2m$ and thus $m\ge 2n$, i.e. a Sprouts game will have at least $2n$ moves [C],[L].
Gaming Aspects
Game Strategy
As stated above, the maximum number of moves in a Sprouts game starting with $n$ nodes equals $3n-1$. The term '$-1$' results from the one node still being alive at the end of the game. More generally, the number $m$ of moves of a Sprouts game is equal to $3n$ minus the number of nodes still being alive in the final position. This leads immediately to an important conclusion: The creation of nodes, which remain alive but are not connectable with other living nodes anymore, controls the number of moves in a Sprouts game. Each player can create such a node $p$ by separating it from other parts of the position using a closed curve. The node $p$ is thus excluded from further play making it dead effectively. Since according to the winning condition the outcome of a game of Sprouts depends on the number of moves [BCG], this approach will also control the game itself. It was used as starting point for the development of winning strategies for specific values of $n$ [FL2]. Nevertheless no general winning strategy has been developed so far.
Game Tree
Sprouts is a finite game. Thus a winning strategy exists for one of the two players. Which player can enforce the win, is still an open question in the general, however. Lacking suitable other techniques, its discussion relies on a construction of the game tree. For $n\le 7$ initial nodes this was done by hand (for $n=7$ look at [FL2]); for games with $n>7$ computer support seems to be mandatory [AJS],[J],[LV1],[LV4].
The algorithmical construction of the game tree is based on a discrete and finite representation of Sprouts positions like the one given in the section formalization. To enable an efficient computation, redundant information sill contained in the description (e.g. renaming of nodes, edges, faces or mirroring a position at a face boundary according to the Jordan curve theorem) has to be minimized. Another important technique for reducing the necessary computation effort is the decomposition of a Sprouts position in independent subpositions whenever possible [LV5]. Despite of all efforts, the question, whether a Sprouts position can continue for more than $k$ moves, remains NP-complete. The same holds for the analogous question, whether a Sprouts position can end in fewer than $k$ moves [BS]. Thus, only small values of $n$ have been checked up to now ($n\le 44$ as of 2011). Tables of the known results can be found here [1]. It is conjectured [AJS] that the first player wins for $n=3,4,5\bmod 6$.
The misère version is analyzed in a similar way. It is conjectured, that here the first player wins for $n=0,4,5\bmod 6$ except for $n=1,4$. Outcomes are only known up to $n=20$, however. The fewer number of data points results from difficulties in the mathematical and computational handling of misère games [Pl],[LV3].
Variants
Brussels Sprouts
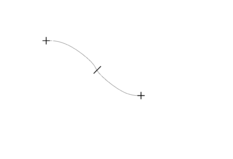
This version of Sprouts uses crosses instead of points [BCG],[CG],[G2]. Each line connecting two crosses (or a cross with itself) must start and end at a free arm of a cross. Anywhere on the new line a cross-bar is added, giving one new free arm at each side of the line. The cross-bar represents a new cross (with two opposing arms used up by the line just drawn).
|
|
|
|
|
|
|
|
|
|
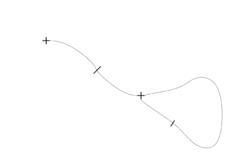
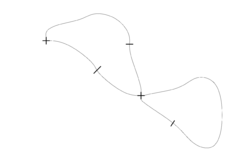
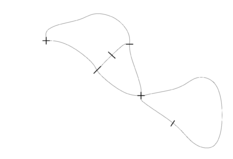
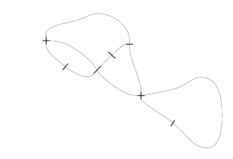
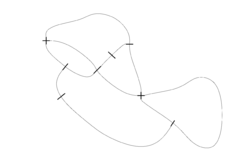
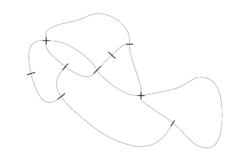
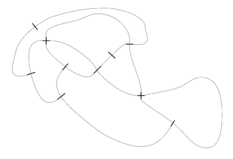
Example: Game of Brussels Sprouts starting with 2 points | ||
The termination of Brussels Sprouts is not obvious, because a move does not change the total number of free arms (two arms are used up, and two new free arms are introduced). However, it can be shown that a game starting with $n$ crosses ends always after $m=5n-2$ moves. To see this, apply the Euler Theorem. It holds:
- The number $v$ of nodes is equal to $n+m$ (Each move adds one cross, i.e. a node).
- The number $e$ of edges is equal to $2m$ (Each move adds two edges).
- The number $f$ of faces is equal to $4n$ (In a final position, each face contains one free arm. A move does not change the total number of free arms. Thus, the number of faces is equal to the number of free arms at the beginning. And at the beginning each cross has 4 free arms).
- The number of connection components is equal to one (Otherwise, it would exist a face $F$ containing nodes --- i.e. crosses --- of two connection components $X, Y$ in its boundary. For both $X$ and $Y$ there must exist at least one such cross with a free arm accessible from $F$. Thus, a move is possible connecting these free arms belonging to $X$ and $Y$ with a line across $F$. This is a contradiction to the assumption that we consider a final position).
For a planar graph, it holds $v-e+f=2$ and thus $n+m-2m+4n=5n-m=2$.
Due to the fixed number of moves (independent from the play), Brussels Sprouts is uninteresting from the gaming perspective. A player only has the freedom to create new separated regions by a closed curve; the rules ('add a cross-bar on the line newly drawn') determine the number of new lives in- and outside of the region to be exactly one. Sprouts, in the contrary, offers the additional freedom to use the single new life added by a new point either inside or outside of a separate region.
Analogous to Sprouts, Brussels Sprouts can be generalized to be played on orientable compact surfaces. On non-orientable compact surfaces, a 'real' game results in this way [CC], whereby winning strategies have been found for some special cases [Gi]. Another interesting option is to make the addition of a new cross in a move optional.
Stars-and-Stripes, also called Cloves
This version of Sprouts is similar to Brussels Sprouts, but stars with $2, 3, 4, \ldots$ arms are allowed in the starting position instead of only crosses with particularly 4 arms [BCG]. In a move, always a 4-arm star (stripe) is added. Winning strategies for special cases are presented in [CC].
Black-and-white Sprouts, also called Weeds
In this version, the player has the choice to add a new dot on the new line drawn in a move or not. It exists a winning strategy for the first player according to [2].
Sprouts on compact surfaces
The game of Sprouts played on a sphere is equivalent to the play on a plane, because the plane is homeomorphic to a punctured sphere. All other compact surfaces can be represented on the plane using the fundamental polygon. In this way, start positions with up to $n=14$ points on orientable compact surfaces with a genus $g\le 9$ were analyzed [LV2]. The results lead to the conjecture that the first player wins for $n=3,4,5\bmod 6$ (as in the plane), independent from $g$. For nonorientable compact surfaces, the resulting pattern (start positions with $n\le 14$ on nonorientable compact surfaces with $g\le 8$ were analyzed) shows a higher complexity. Tables of the known results (for both normal and misère play) can be found on [3].
An interesting theoretical result in this respect is the following: For a given $n$ it suffices to solve the game for compact surfaces up to a certain limiting genus, if one wants to formulate a winning strategy for compact surfaces of arbitrary genus.
Sorokins Game
Sprouts is played on a sheet of paper, considering a specific embedding of the developing graph. Sorokins game instead is played with the constraint, that the developing graph must remain embeddable in the plane. In other words, graphs admissable in Sorokins game are planar (and have nodes with degree $\le 3$).
Antwerp Sprouts
Antwerp Sprouts is played with colored points. For the rules of two different versions, see [4].
Another generalization
A move in Sprouts consists of adding a new point and connecting it with the already existing points using 2 edges. A possible generalization is to use always $q$ edges, $q\ge 2$, instead of specifically $q=2$, and allow graphs of maximum degree $p$ (see [5]). For e.g. $p=4$, $q=3$ this results in games with at most $2n-1$ moves. Correspondigly, the choice $p=5$, $q=3$ leads to games with at most $5n-2$ moves.
References
| [AJS] | D. Applegate, G. Jacobson, and D. Sleator, " Computer analysis of Sprouts", Carnegie Mellon University Computer Science Technical Report No. CMU-CS-91-144, May 1991 |
| [BS] | L. Baird III, D. Schweitzer, "Complexity of the Game of Sprouts", FCS'10 (6th International Conference on Foundations of Computer Science), Las Vegas 2010 |
| [BCG] | E. Berkelamp, J. Conway, R. Guy, "Winning Ways for your Mathematical Plays", vol. 2, Academic Press, London, 1982, chapter 17, pp. 564-568 |
| [CC] | G. Cairns, K. Chartarrayawadee, "Brussels Sprouts and Cloves", Mathematics Magazine 80(2007) February pp.46-58 |
| [C] | M. Copper, "Graph theory and the game of Sprouts", American Mathematical Monthly 100(1993)478-482 |
| [DHKR] | J. Draeger, S. Hahndel, G. Koestler, P. Rosmanith, "Sprouts: Formalisierung eines topologischen Spiels", Technical Report TUM-I9015, Technische Universität München 1990 |
| [FL1] | R. Focardi, F. Luccio, "A new analysis technique for the Sprouts Game", FUN 2001 (2nd Convegno International Conference on Fun with Algorithms), Isola d’Elba 2001, Ed. Carleton Scientific, pp. 117-132 |
| [FL2] | R. Focardi, F. Luccio, "A modular approach to Sprouts", Discrete Applied Mathematics 144 (2004)303-319 |
| [G1] | M. Gardner, "Mathematical games: of sprouts and brussels sprouts, games with a topological flavor", Scientific American 217(1967), July 112-115 |
| [G2] | M. Gardner, "Sprouts and Brussels Sprouts", in M. Gardener, "Mathematical Carnival", Mathematical Association of America 1989 |
| [Gi] | P.J. Giblin, Graphs, surfaces and homology, Second edition, Chapman \& Hall, London, 1981. |
| [J] | Josh Jordan |
| [L] | T.K. Lam, "Connected sprouts", American Mathematical Monthly 104(1997) February 116-119 |
| [LV1] | J. Lemoine, S. Viennot, "A further computer analysis of sprouts", draft, 2007 |
| [LV2] | J. Lemoine, S. Viennot, "Sprouts games on compact surfaces", arXiv:0812.0081v2 [math.CO] 2 Mar 2009 |
| [LV3] | J. Lemoine, S. Viennot, "Analysis of misère Sprouts game with reduced canonical trees", arXiv:0908.4407v1 [math.CO] 30 Aug 2009 |
| [LV4] | J. Lemoine, S. Viennot, "Computer analysis of Sprouts with nimbers", arXiv:1008.2320v1 [math.CO] 13 Aug 2010 |
| [LV5] | J. Lemoine, S. Viennot, "Nimbers are inevitable", arXiv:1011.5841v1 [math.CO] 26 Nov 2010 |
| [Pl] | T. Plambeck, "Advances in Losing", arXiv:math/0603027v1 [math.CO] 1 Mar 2006 |
| [Pr] | G. Pritchett, "The game of Sprouts", Two-Year College Mathematics Journal 7(1976) December 21-25 |
Sprouts. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sprouts&oldid=51614