Spline approximation
The approximate representation of a function, or the approximate reconstruction of a function in a given class from incomplete information (for example, from its values on a set of points), using splines (cf. Spline).
As in the classical theory of approximation of functions, one studies linear methods of spline approximation (including spline interpolation), best methods, and also approximations by classes of non-linear splines, such as splines with variable knots.
Best approximation by splines.
This involves questions of existence and uniqueness, as well as characteristic properties of a spline of best approximation (see Element of best approximation), along with the order of approximation, and asymptotic and exact upper bounds for the deviation of splines from a given class of functions. Splines with fixed knots do not form a Chebyshev system; accordingly, a spline of best approximation need not be unique in $ C [ a , b ] $, and the characteristic properties of splines of best approximation are more complex than the characteristic properties of the polynomial of best approximation (see [8]). However, in $ L [ a , b ] $, for the subclass of continuous functions, splines of best approximation do have uniqueness properties in the case when they are tied together from smooth functions to form a Chebyshev system on $ [ a , b ] $( see [2]). Splines with fixed smoothness properties but with non-fixed knots (where it is assumed, however, that the number of knots does not exceed a given number) do not form a closed set, and so splines of best approximation need not exist in this case. The order of approximation can be characterized by the following result [6]:
$$ \tag{1 } \| f ^ { ( i) } ( x) - S _ {m , \Delta _ {n} } ^ {(} i) ( x) \| _ {L _ {p} [ a , b ] } \leq $$
$$ \leq \ c \| \Delta _ {n} \| ^ {1 - p ^ {-} 1 + q ^ {-} 1 } \omega _ {m-} i ( f ^ { ( i+ 1) } , \| \Delta _ {n} \| ) _ {q} , $$
$$ 1 \leq p \leq q \leq \infty , $$
where $ S _ {m ; \Delta _ {n} } ( x) $ is a polynomial spline of degree $ m $ with knots at the points of the partition
$$ \Delta _ {n} : a = x _ {0} ^ {(} n) \leq \ x _ {1} ^ {(} n) < \dots < x _ {n} ^ {(} n) = b , $$
$$ \| \Delta _ {n} \| = \max _ {0 \leq i \leq n - 1 } ( x _ {i+} 1 - x _ {i} ) , $$
$ \omega _ {k} ( f , \delta ) _ {q} $ is the modulus of smoothness of order $ k $ in $ L _ {q} [ a , b ] $( cf. Smoothness, modulus of), and $ f $ is a function with absolutely-continuous $ ( l - 1 ) $- st derivative and with $ l $- th derivative in $ L _ {q} $( $ 1 \leq l \leq m $), $ i = 0 \dots l - 1 $. When $ 1 \leq q \leq p \leq \infty $, one can replace $ i $ by $ i - 1 $ in (1) and remove the constant $ \| \Delta _ {n} \| ^ {1 - p ^ {-} 1 + q ^ {-} 1 } $. Weaker analogues of (1) have been obtained for multi-dimensional splines. For example, if $ f \in W _ {2} ^ {k} ( \Omega ) $( a Sobolev space), $ S _ {n} ^ {k} $ is the set of splines (of degree at most $ k $ in every variable) with uniform knots and width $ h $, and if the domain $ \Omega $ satisfies the strict cone condition (see Imbedding theorems), then
$$ \inf _ {S \in S _ {h} ^ {k} } \ \| f - S \| _ {W _ {2} ^ {j} ( \Omega ) } \leq c \cdot h ^ {k-} j \| f \| _ {W _ {2} ^ {k} ( \Omega ) } ,\ \ 0 \leq j \leq k . $$
For the uniform partition $ ( \| \Delta _ {n} \| = 1 / n ) $ and the class $ W _ {q} ^ {m+} 1 $, the order of the right-hand side of (1) equals $ n ^ {p ^ {-} 1 - q ^ {-} 1 - m - 1 + i } $ when $ 1 \leq p \leq q \leq \infty $. If one considers approximation by splines of degree $ m $, of smoothness $ m - 1 $, with variable knots, the number of which does not exceed $ n $, then it can be shown [7] that at the expense of the choice of knots, the order of approximation is equal to $ n ^ {- m - 1 + i } $. For the best uniform approximation of some classes of periodic functions by polynomial splines with uniform knots there is a series of final results. For example, for the class $ \widetilde{W} {} ^ {r} H _ \omega $, where $ \omega ( \delta ) $ is the convex modulus of continuity, the least upper bound of the deviation from splines of degree $ r $ has been determined [4]; it coincides with the corresponding width of this class. Best approximation by splines with further restrictions on higher derivatives has also been studied [6]. The problem of best approximation of the special function $ ( b - t ) ^ {r} $ arises naturally (see Monospline) in the study of best quadrature formulas.
Linear methods of approximation by splines.
These methods were studied before problems of best approximation by splines, and attention has centred on approximation by interpolation splines (cf. Interpolation spline; see [1], [3], [5]). These often give the same order of approximation as splines of best approximation, which is one of the advantages over interpolation by polynomials. Thus, if a function has a continuous $ r $- th derivative on $ ( - \infty , \infty ) $, then one has the following estimate [6] for the approximation by polynomial interpolation splines $ S _ {n} ( x , h ) $ of degree $ n \geq r $ with uniform interpolation knots $ x _ {i} = i h $, $ i = 0 , \pm 1 , \pm 2 \dots $ and uniform spline knots:
$$ \| f ^ { ( i) } ( x) - S _ {n} ^ {(} i) ( x , h ) \| _ {C ( - \infty , \infty ) } \leq $$
$$ \leq \ c \cdot \omega _ {r+} 1- i ( f ^ { ( i) } , h ) ,\ i = 0 \dots r. $$
In the study of interpolation splines with arbitrary knots, one selects as parameter of approximation the maximal distance between the interpolation knots (usually, interpolation knots and spline knots are closely related). In applications, the most widely-used splines are the polynomial interpolation splines $ S _ {3} ( x) $ of degree three, the cubic splines. This is related to the fact that the construction of such splines can usually be reduced to the solution of a system of linear equations with a tri-diagonal matrix having a dominant main diagonal. The solution of such a system can easily be performed on a computer. If, in addition, the function $ f $ has a continuous $ k $- th derivative on $ [ a , b ] $( $ 0 \leq k \leq 3 $), then one has the following estimates:
$$ \| f ^ { ( i) } ( x) - S _ {3} ^ {(} i) ( x) \| _ {C [ a , b ] } \leq $$
$$ \leq \ c \| \Delta _ {n} \| ^ {k-} i \omega ( f ^ { ( k) } , \| \Delta _ {n} \| ) ,\ 0 \leq i \leq k , $$
where the $ x _ {i} ^ {(} n) $ are the interpolation knots. When $ k = 1 $ or $ 2 $, the constant $ c > 0 $ does not depend on $ f $ or on the partition $ \Delta _ {n} $. When $ k = 0 $ or $ k = 3 $, further restrictions are imposed on the sequence of partitions $ \Delta _ {n} $. Analogous results hold for multi-dimensional cubic splines, and also for splines of higher degree.
Interpolation splines of odd degree have several extremal properties. For example, consider the class of functions having an absolutely-continuous $ ( m - 1 ) $- st derivative on $ [ a , b ] $, an $ m $- th derivative in $ L _ {2} [ a , b ] $, and pre-assigned values $ y _ {i} $ at points $ x _ {i} $, $ a < x _ {0} < \dots < x _ {n} < b $. Among these, the function whose $ m $- th derivative has smallest $ L _ {2} $- norm on $ [ a , b ] $ is the polynomial spline $ S _ {2m-} 1 ( x) $ with knots $ x _ {i} $, which takes values $ y _ {i} $ at the points $ x _ {i} $, has a continuous $ ( 2 m - 2 ) $- nd derivative on $ [ a , b ] $, and coincides on $ [ a , x _ {0} ] $ and $ [ x _ {n} , b ] $ with polynomials of degree at most $ m - 1 $. This property has served as a basis for numerous generalizations of splines. For some classes of functions, the least upper bound of the deviation from interpolation splines coincides with that for splines of best approximation. This assertion holds, for example, for the class $ \widetilde{W} {} ^ {r} H _ \omega $ when $ \omega ( \delta ) = \delta $.
Splines play an important role in the problem of smoothing ([3], [5]) grid functions given with some error. They are used to construct bases [5] and orthonormal bases [9] with bounded Lebesgue constants.
Methods of spline approximation are closely connected with the numerical solution of partial differential equations by the finite-element method, which is based on the Ritz method with a special choice of basis functions. In this method, one chooses piecewise-polynomial functions (i.e. splines, cf. Spline) as basis functions. For example, let $ \Omega $ be a bounded domain in $ \mathbf R ^ {2} $ which can be decomposed into a finite number of right-triangular subdomains $ T _ {i} $, $ 1 \leq i \leq N $. For a fixed $ i $ the polynomial
$$ P _ {i} ( x _ {1} , x _ {2} ) = \alpha _ {1} + \alpha _ {2} x _ {1} + \alpha _ {3} x _ {2} + \alpha _ {4} x _ {1} ^ {2} + \alpha _ {5} x _ {1} x _ {2} + \alpha _ {6} x _ {2} ^ {2} $$
is defined by the conditions
$$ P _ {i} ( p _ {ij} ) = f ( p _ {ij} ) ,\ \ P _ {i} ( q _ {ij} ) = f ( q _ {ij} ) ,\ \ j = 1 , 2 , 3 , $$
where the function $ f ( p) $ is continuous on $ \overline \Omega \; $, $ p _ {ij} $ are the vertices of the triangle $ T _ {i} $ and $ q _ {ij} $ are the mid-points of its sides. Let $ S ( p) = P _ {i} ( p) $ for $ p \in T _ {i} $, $ i = 0 \dots N $. If $ f \in W _ {2} ^ {3} ( \Omega ) $, then
$$ \| f - S \| _ {W _ {2} ^ {j} ( \Omega ) } \leq c h ^ {3-} j \| f \| _ {W _ {2} ^ {3} ( \Omega ) } ,\ \ j = 0 , 1 , $$
where $ h $ is the length of a side of $ T _ {i} $ and $ c $ is an absolute constant.
References
| [1] | J.H. Ahlberg, E.N. Nilson, J.F. Walsh, "Theory of splines and their applications" , Acad. Press (1967) |
| [2] | P.V. Galkin, "The uniqueness of the element of best mean approximation to a continuous function using splines with fixed nodes" Math. Notes , 15 : 1 (1974) pp. 3–8 Mat. Zametki , 15 : 1 (1974) pp. 3–14 |
| [3] | V.L. Miroshnichenko, "Methods of spline functions" , Moscow (1980) |
| [4] | N.P. Korneichuk, "On uniform approximation of periodic functions by subspaces of finite dimension" Soviet Math. Dokl. , 14 : 6 (1973) pp. 1736–1741 Dokl. Akad. Nauk SSSR , 213 : 3 (1973) pp. 525–528 |
| [5] | S.B. Stechkin, Yu.N. Subbotin, "Splines in numerical mathematics" , Moscow (1976) (In Russian) |
| [6] | Yu.N. Subbotin, "Extremal functional interpolation and approximation by splines" Math. Notes , 16 : 5 (1974) pp. 1097–1103 Mat. Zametki , 16 : 5 (1974) pp. 843–854 |
| [7] | Yu.N. Subbotin, N.I. Chernych, "Order of the best spline approximations of some classes of functions" Math. Notes , 7 (1970) pp. 20–26 Mat. Zametki , 7 : 1 (1970) pp. 31–42 |
| [8] | L.L. Schumaker, "Uniform approximation by Tchebycheffian spline functions" J. Math. and Mech. , 18 (1968) pp. 369–377 |
| [9] | Z. Ciesielski, J. Domsta, "Construction of an orthonormal basis in 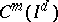 and and 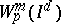 " Studia Math. , 41 (1972) pp. 211–224 " Studia Math. , 41 (1972) pp. 211–224 |
Comments
References
| [a1] | T.N.E. Greville (ed.) , Theory and application of spline functions , Acad. Press (1969) |
| [a2] | I.J. Schoenberg (ed.) , Approximations with special emphasis on spline functions , Acad. Press (1969) |
| [a3] | P.M. Prenter, "Splines and variational methods" , Wiley (1975) |
| [a4] | C. de Boor, "A practical guide to splines" , Springer (1978) |
| [a5] | Z. Cieselski, "Spline bases in function spaces" Z. Cieselski (ed.) J. Musielak (ed.) , Approximation theory , Reidel (1975) pp. 49–54 |
| [a6] | K. Böhmer (ed.) G. Meinardus (ed.) W. Schempp (ed.) , Spline-Funktionen , B.I. Wissenschaftsverlag Mannheim (1974) |
Spline approximation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spline_approximation&oldid=48783