Sine
One of the trigonometric functions:
$$y=\sin x.$$
The domain of definition is the whole real line and the range of values is the interval $[-1,1]$. The sine is an odd periodic function of period $2\pi$. Sine and cosine are connected by the formula
$$\sin^2x+\cos^2x=1.$$
Sine and cosecant are connected by the formula
$$\sin x=\frac{1}{\operatorname{cosec}x}.$$
The derivative of sine is:
$$(\sin x)'=\cos x.$$
The indefinite integral of sine is:
$$\int\sin(x)\,dx=-\cos x+C.$$
Sine has the following power series representation:
$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\dotsb,\qquad-\infty<x<\infty.$$
The function inverse to sine is called arcsine.
The sine and cosine of a complex argument $z$ are related to the exponential function by Euler's formulas:
$$e^{iz}=\cos z+i\sin z,\\\sin z=\frac{e^{iz}-e^{-iz}}{2i},$$
and if $z=ix$ is pure imaginary, then
$$\sin ix=-\sinh x,$$
where $\sinh x$ is the hyperbolic sine.
Comments
Of course, $\sin x$ can be defined by the Euler formulas or by its power series. A visual definition runs as follows. Consider the unit circle with centre at the origin $O$ in a rectangular coordinate system and with a rotating radius vector $OP$. Let $x$ be the angle between $OA$ and $OP$ (being reckoned positive in the counter-clockwise direction) and let $P'$ be the projection of $P$ on $OA$. Then $\sin x$ is defined as the ratio $(PP')/(OP)$, $\cos x$ as the ratio $(OP')/(OP)$ and $\tan x$ as the ratio $(PP')/(OP')$.
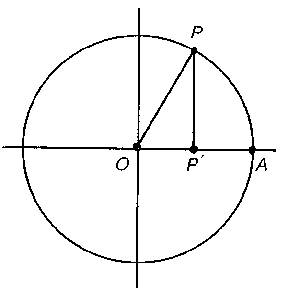
Figure: s085480a
Another, analytical, approach starts with the function $\phi$ defined on the closed interval $[-1,1]$ by $\phi(x)=\int_0^xdt/\sqrt{1-t^2}$. For $x=\pm1$ this integral is improper, but convergent. It is easy to see that $\phi$ is monotone increasing and continuous on the closed interval $[-1,1]$ and differentiable on the open interval $(-1,1)$, and has values in $[-\pi/2,\pi/2]$. So it has an inverse function, defined on $[-\pi/2,\pi/2]$, with values in $[-1,1]$. This function is called $\sin x$, and it can be proved that the domain of definition of this function can be continued to the whole real axis. The function $\phi$ is called arcsine.
The graph of $\sin x$ is the sinusoid (see also Trigonometric functions).
References
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) pp. §4.3 |
Sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sine&oldid=44643