Semi-cubic parabola
From Encyclopedia of Mathematics
2020 Mathematics Subject Classification: Primary: 53A04 [MSN][ZBL]
A third-order algebraic curve in the plane whose equation in Cartesian coordinates is
$$y=ax^{3/2}.$$
The origin is a cusp (see Fig.). The length of the arc from the origin equals
$$l=\frac{1}{27a^2}[(4+9a^2x)^{2/3}-8];$$
and the curvature equals
$$k=\frac{6a}{\sqrt x(4+9a^2x)^{3/2}}.$$
A semi-cubic parabola is sometimes called a Neil parabola, after W. Neil who found its arc length in 1657.
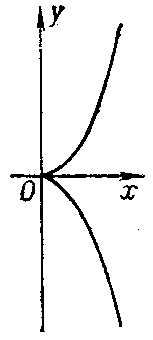
Figure: s084040a
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
How to Cite This Entry:
Semi-cubic parabola. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-cubic_parabola&oldid=43172
Semi-cubic parabola. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-cubic_parabola&oldid=43172
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article