Sector in the theory of ordinary differential equations
An open curvilinear sector $ S $
with vertex at an isolated singular point $ O $
of an autonomous system of second-order ordinary differential equations
$$ \tag{* } \dot{x} = f ( x),\ \ x \in \mathbf R ^ {2} , $$
$ f \in C ( G) $, where $ G $ is the domain of uniqueness, that satisfies the following four conditions: 1) each lateral boundary of $ S $ is a $ TO $- curve of the system (*) (i.e. a semi-trajectory that approaches $ O $ as $ | t | \rightarrow + \infty $, and touches a certain direction at $ O $); 2) the outer boundary of $ S $ is a simple parametric arc (the homeomorphic image of a closed interval); 3) $ \overline{S}\; \setminus \{ 0 \} $ does not contain singular points of (*). The fourth condition is one of the following three: 4a) all trajectories of the system (*) that start in $ S $ leave this sector for both increasing and decreasing $ t $; such a sector is called a hyperbolic sector, or a saddle sector (Fig. a); 4b) all trajectories of (*) that start in $ S $ sufficiently near $ O $ do not leave $ S $ but approach $ O $ as $ t $ increases, and as $ t $ decreases they leave $ S $( or vice-versa); such a sector is called a parabolic sector or an open node sector (Fig. b); or 4c) all the trajectories of (*) that start in $ S $ sufficiently near $ O $ do not leave $ S $ as $ t $ increases or decreases but approach $ O $, forming together with $ O $ closed curves (loops), and for any two loops one encloses the other; such a sector is called an elliptic sector or a closed node sector (Fig. c).

Figure: s083770a

Figure: s083770b

Figure: s083770c
For any analytic system (*) with $ TO $- curves, a disc $ Q $ of sufficiently small radius and centre at $ O $ can always be divided into a finite number of sectors of a specific form: $ h $ hyperbolic, $ p $ parabolic and $ e $ elliptic ones (see [1] and [2]). The Frommer method can be used to exhibit all these sectors, to determine the type of each, and to establish the rules of their succession in a circuit about $ O $ along the boundary of $ Q $( and thereby to show the topological structure of the arrangement of the trajectories of (*) in a neighbourhood of $ O $). There are a priori estimates from above for $ h $, $ p $ and $ e $ in terms of the order of smallness of the norm $ \| f ( x) \| $ as $ x \rightarrow 0 $( see [1], [4], [5]).
Sometimes (see, for example, [3]) the notion of a "sector" is defined more freely: In hyperbolic and parabolic sectors loops are allowed that cover a set without limit points on the rear boundary of a sector, and in elliptic sectors, loops that do not contain one another. Here the first sentence of the previous paragraph remains valid also for a system (*) of general form, and the Poincaré index $ i $ of the singular point $ O $ of (*) is expressed by Bendixson's formula
$$ i = 1 + \frac{e - h }{2} . $$
References
| [1] | I. Bendixson, "Sur des courbes définiés par des équations différentielles" Acta Math. , 24 (1901) pp. 1–88 |
| [2] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Qualitative theory of second-order dynamic systems" , Wiley (1973) (Translated from Russian) |
| [3] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [4] | A.N. Berlinskii, "On the structure of the neighborhood of a singular point of a two-dimensional autonomous system" Soviet Math. Dokl. , 10 : 4 (1969) pp. 882–885 Dokl. Akad. Nauk SSSR , 187 : 3 (1969) pp. 502–505 |
| [5] | M.E. Sagalovich, "Classes of local topological structures of an equilibrium state" Diff. Equations , 15 : 2 (1979) pp. 253–255 Differentsial'nye Urnveniya , 15 : 2 (1979) pp. 360–362 |
Comments
The lateral boundaries are sometimes called base solutions.
A Frommer sector, or Frommer normal domain, is a circular sector
$$ N = \ \{ {( r, \phi ) } : {0 < r \leq \delta ,\ | \phi - \phi _ {0} | \leq \epsilon } \} $$
with vertex at an isolated point $ O $( $ x = x _ {0} $) of the system
(see 1)) with lateral boundary $ OA $ and $ OB $, $ \phi _ {A} = \phi _ {0} - \epsilon $, $ \phi _ {B} = \phi _ {0} + \epsilon $, and with the rear boundary $ AB $ satisfying the following conditions (here $ r $ and $ \phi $ are polar coordinates in the $ x $- plane with pole at $ O $, and $ \delta , \epsilon , \phi _ {0} \in \mathbf R $):
A) $ \phi = \phi _ {0} $ is an exceptional direction of the system
at $ O $, that is, there is a sequence $ x _ {k} = x _ {0} + ( r _ {k} \cos \phi _ {k} , r _ {k} \sin \phi _ {k} ) $, $ k = 1 \dots $ $ r _ {k} \rightarrow 0 $, $ \phi _ {k} \rightarrow \phi _ {0} $ as $ k \rightarrow + \infty $, such that if $ \alpha ( x) $ is the angle between the directions of the vectors $ f ( x) $ and $ x - x _ {0} $, then $ \mathop{\rm tan} \alpha ( x _ {k} ) \rightarrow 0 $ as $ k \rightarrow + \infty $, and this direction is unique in $ N $;
B) $ \mathop{\rm tan} \alpha ( x) \neq 0 $ for any $ x \in OA \cup OB $;
C) $ \alpha ( x) \neq \pi /2 $ for any $ x \in N $.
Suppose that the angle $ \alpha ( x) $ is measured from the vector $ x - x _ {0} $ and has the sign of the reference direction. A sector $ N $ is called a Frommer normal domain of the first type (notation: $ N _ {1} $) if $ \mathop{\rm tan} \alpha ( x) < 0 $ for $ x \in OA $ and $ \mathop{\rm tan} \alpha ( x) > 0 $ for $ x \in OB $; a normal domain of the second type (notation: $ N _ {2} $) if $ \mathop{\rm tan} \alpha ( x) > 0 $ on $ OA $ and $ \mathop{\rm tan} \alpha ( x) < 0 $ on $ OB $; and a normal domain of the third type $ ( N _ {3} ) $ if $ \mathop{\rm tan} \alpha ( x) $ has one and the same sign on $ OA $ and on $ OB $. These domains were introduced by M. Frommer [1].
The trajectories of the system
in Frommer normal domains behave as follows. The domain $ N _ {1} $ is covered by $ O $- curves of the system (Fig. d). They form an open pencil (cf. Sheaf 2)), that is, a family of $ O $- curves of the same type that depends continuously on a parameter which varies over an open interval. In the domain $ N _ {2} $ there is either a) a unique $ O $- curve (Fig. e), or b) infinitely many $ O $- curves (a closed pencil; cf. Fig. f). In the domain $ N _ {3} $, either a) there are infinitely many $ O $- curves (a semi-open pencil; Fig. g) or b) there are no $ O $- curves (Fig. h).
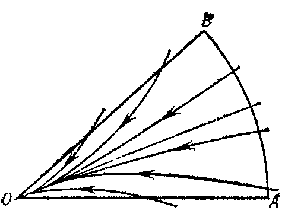
Figure: s083770d
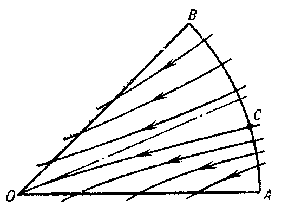
Figure: s083770e
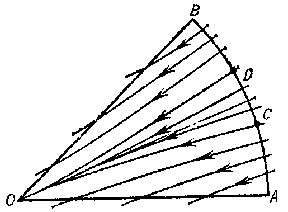
Figure: s083770f
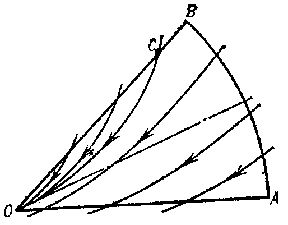
Figure: s083770g

Figure: s083770h
In a normal domain $ N $ of any type the $ O $- curves tend to $ O $ along the direction $ \phi = \phi _ {0} $ as $ t \rightarrow + \infty $( or $ t \rightarrow - \infty $), and with decreasing (increasing) $ t $ they leave the domain $ N $; all other trajectories leave $ N $ for both increasing and decreasing $ t $. The problems of distinguishing between the cases a) and b) for domains $ N _ {2} $ and $ N _ {3} $ are called, respectively, the first and second distinction problems of Frommer.
If a system
has at $ O $ a finite number $ (> 0) $ of exceptional directions, each of which can be included in a normal domain $ N $, and if for all domains $ N _ {2} $ and $ N _ {3} $ Frommer's distinction problems are solvable, then the topological structure of the arrangement of the trajectories of the system in a neighbourhood of $ O $ is completely explained, because the sectors with vertex $ O $ that are positioned between normal domains are, sufficiently close to $ O $, entirely intersected by the trajectories of the system (as in Fig. h). Such a situation holds, for example, when
$$ f ( x) = P ( x) + p ( x),\ \ P = ( P _ {1} , P _ {2} ), $$
where $ P _ {1} $ and $ P _ {2} $ are forms of degree $ n \geq 1 $ in the components $ x _ {1} , x _ {2} $ of the vector $ x $,
$$ p ( x) = o ( \| x \| ^ {n} ) \ \ \textrm{ as } \| x \| \rightarrow 0, $$
and when the following conditions are fulfilled: The form $ x _ {1} P _ {2} ( x) - x _ {2} P _ {1} ( x) $ has real linear factors, the forms $ P _ {1} $ and $ P _ {2} $ do not have common real linear factors, and $ p \in C ^ {n + 1 } $. Here situation a) holds in each of the domains $ N _ {2} $, $ N _ {3} $.
Analogues of Frommer normal domains have been introduced for systems of the form
of order $ \geq 3 $.
References
| [1] | M. Frommer, "Die Integralkurven einer gewöhnlichen Differentialgleichung erster Ordnung in der Umgebung rationaler Unbestimtheitsstellen" Math. Ann. , 99 (1928) pp. 222–272 |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [3] | A.F. Andreev, "A uniqueness theorem for a normal region of Frommer's second type" Soviet Math. Dokl. , 3 : 1 (1962) pp. 132–135 Dokl. Akad. Nauk SSSR , 142 : 4 (1962) pp. 754–757 |
| [4] | A.F. Andreev, "Strengthening of the uniqueness theorem for an 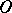 -curve in -curve in 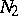 " Soviet Math. Dokl. , 3 : 5 (1962) pp. 1215–1216 Dokl. Akad. Nauk SSSR , 146 : 1 (1962) pp. 9–10 " Soviet Math. Dokl. , 3 : 5 (1962) pp. 1215–1216 Dokl. Akad. Nauk SSSR , 146 : 1 (1962) pp. 9–10 |
Sector in the theory of ordinary differential equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sector_in_the_theory_of_ordinary_differential_equations&oldid=48642