Search algorithm
on a graph, graph search
An algorithm that tries to find all nodes in a network or graph that satisfy a given property. Such algorithms are also used, e.g., to optimize a function on a graph or network or on a set which can easily be turned into a graph, such as $ \{ 0,1 \} ^ {n} $. (Two $ 0 $- $ 1 $ vectors of length $ n $ are joined if an only if they differ in precisely one coordinate, yielding a hypercube.) Thus, these are definite relations and similarities between graph search and search theory as a systematic optimization technique (of enumeration type) [a3]. See [a4] for a very complete overview of global optimization (from the search point of view, including random search).
Two of the most often used search techniques in graphs or networks are depth-first search and breadth-first search. Let $ \Gamma = ( V,E ) $ be a finite oriented graph (cf. Graph, oriented). For each $ v \in V $, let $ A ( v ) $ be the set of edges (arcs) issuing from $ v $. For instance, in Fig.a1, $ A ( 1 ) = \{ ( 1,2 ) , ( 1,4 ) \} $, $ A ( 3 ) = \{ ( 3,6 ) \} $, $ A ( 7 ) = \emptyset $.
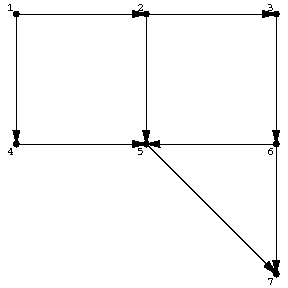
Figure: s110070a
It is assumed that the sets $ A ( v ) $, $ v \in V $, are given some fixed total order (cf. also Totally ordered set) for all $ v $. The following algorithm picks out all nodes in $ \Gamma $ that are reachable from a source node $ s $ by means of a directed path. These nodes will be marked. Central to the algorithm is a certain list $ L $, which can be seen as a sort of wave front indicating the boundary of the spreading blob of marked points:
unmark all points;
mark the source node $ s $;
set $ L = \{ s \} $;
as long as $ L $ is non-empty, run the following iterative procedure:
choose a node $ i \in L $;
select the first oriented edge $ ( i,j ) \in A ( i ) $ that runs (from $ i $) to an unmarked node $ j $( if any);
mark the node $ j $;
define the function $ { \mathop{\rm revp} } $ on $ j $ as $ { \mathop{\rm revp} } ( j ) = i $;
add $ j $ to $ L $;
if there is no $ ( i,j ) \in A ( i ) $ that runs to an unmarked node $ j $, remove $ i $ from $ L $.
stop when $ L $ is empty.
The algorithm does not yet specify how to select a node from $ L $. If $ L $ is treated as a queue, i.e., the node selected is the one that has been longest in $ L $( first-in-first-out) the result is breadth-first search. On the other hand, if $ L $ is treated as a stack, i.e., the node selected is the one that was last added to $ L $( last-in-first-out) the result is depth-first search.
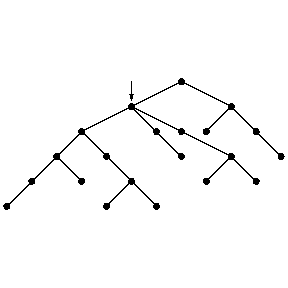
Figure: s110070b
For an oriented tree as in Fig.a2 (downwards oriented), starting at the indicated node, breadth-first search will first pick the three children of the node indicated (in some order) and then will proceed to the next layer. Depth-first search will first pick a maximal downward chain (maximal in the sense that it ends at a leaf, not necessarily maximal in length) and then go back to another child of the last branching node in that chain.
The order which is used on the edge sets $ A ( v ) $ also matters, but not as much.
The edges picked out by the function $ { \mathop{\rm revp} } $( reverse path), i.e., the edges $ ( { \mathop{\rm revp} } ( j ) ,j ) $ form an oriented tree comprising the reachable nodes from the source node $ s $.
The results of the algorithm in four cases are given below for the case of Fig.a1.
<tbody> </tbody>
|
There is an obvious analogous search algorithm for non-oriented graphs. These algorithms run in $ O ( \# V + \# E ) $ time.
References
| [a1] | R.K. Ahuja, T.L. Magnanti, J.B. Orlin, "Network flows" G.L. Nemhauser (ed.) A.H.G. Rinnooy Kan (ed.) M.J. Todd (ed.) , Optimization , North-Holland (1991) pp. 211–370 |
| [a2] | H.M. Salkin, "Integer programming" , Addison-Wesley (1975) |
| [a3] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982) |
| [a4] | A.A. Zhigljavsky, "Theory of global random search" , Kluwer Acad. Publ. (1991) (In Russian) |
Search algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Search_algorithm&oldid=48636