Saddle-node bifurcation
Consider an autonomous system of ordinary differential equations depending on a parameter
$$ \tag{a1 } {\dot{x} } = f ( x, \alpha ) , \quad x \in \mathbf R ^ {n} , \alpha \in \mathbf R ^ {1} , $$
where $ f $ is a smooth function. Suppose that at $ \alpha = 0 $ the system (a1) has an equilibrium (cf. also Equilibrium position) $ x = 0 $ with a simple eigenvalue $ \lambda _ {1} = 0 $( cf. also Eigen value) of its Jacobian matrix $ A = f _ {x} ( 0,0 ) $. Then, generically, two equilibria collide, form a saddle node singular point, and disappear when $ \alpha $ passes through $ \alpha = 0 $. This phenomenon is called the saddle-node (or fold) bifurcation [a1], [a2], [a4]. It is characterized by one bifurcation condition $ \lambda _ {1} = 0 $( has codimension one) and appears generically in one-parameter families.
To formulate relevant facts more precisely, first consider a smooth differential equation
$$ \tag{a2 } {\dot{x} } = f ( x, \alpha ) , \quad x \in \mathbf R ^ {1} , \alpha \in \mathbf R ^ {1} , $$
that has at $ \alpha = 0 $ the equilibrium $ x = 0 $ with $ \lambda _ {1} = f _ {x} ( 0,0 ) = 0 $. If the following non-degeneracy (genericity) conditions hold:
1) $ a = ( {1 / 2 } ) f _ {xx } ( 0,0 ) \neq 0 $;
2) $ f _ \alpha ( 0,0 ) \neq 0 $, then (a2) is locally topologically equivalent (cf. Equivalence of dynamical systems) near the origin to the normal form
$$ \tag{a3 } {\dot{y} } = \beta + \sigma y ^ {2} , \quad y \in \mathbf R ^ {1} , \beta \in \mathbf R ^ {1} , $$
where $ \sigma = { \mathop{\rm sign} } a = \pm 1 $, [a2], [a6]. The system (a3) has two equilibria (one stable and one unstable) $ y _ {1,2 } = \pm \sqrt {- \sigma \beta } $ for $ \sigma \beta < 0 $ and no equilibria for $ \sigma \beta > 0 $.
In the $ n $- dimensional case, the Jacobian matrix $ A $ evaluated at the equilibrium $ x = 0 $ has a simple eigenvalue $ \lambda _ {1} = 0 $, as well as $ n _ {s} $ eigenvalues with $ { \mathop{\rm Re} } \lambda _ {j} < 0 $, and $ n _ {u} $ eigenvalues with $ { \mathop{\rm Re} } \lambda _ {j} > 0 $( $ n _ {s} + n _ {u} + 1 = n $). According to the centre manifold theorem (cf. Centre manifold; [a5], [a3], [a7]), there is an invariant one-dimensional centre manifold $ {\mathcal M} _ \alpha $ near the origin, the restriction of (a1) to which has the form (a2). Moreover, [a2], under the non-degeneracy conditions 1) and 2), the system (a1) is locally topologically equivalent (cf. Equivalence of dynamical systems) near the origin to the suspension of the normal form (a3) by the standard saddle:
$$ \tag{a4 } \left \{ \begin{array}{l} { {\dot{y} } = \beta + \sigma y ^ {2} , \ y \in \mathbf R ^ {1} , \beta \in \mathbf R ^ {1} , } \\ { {\dot{y} } _ {s} = - y _ {s} , \ y _ {s} \in \mathbf R ^ {n _ {s} } , } \\ { {\dot{y} } _ {u} = + y _ {u} , \ y _ {u} \in \mathbf R ^ {n _ {u} } . } \end{array} \right . $$
Fig.a1 shows the phase portraits of the system (a4) in the planar case, when $ n = 2 $, $ n _ {s} = 1 $, $ n _ {u} = 0 $, and $ \sigma = 1 $.
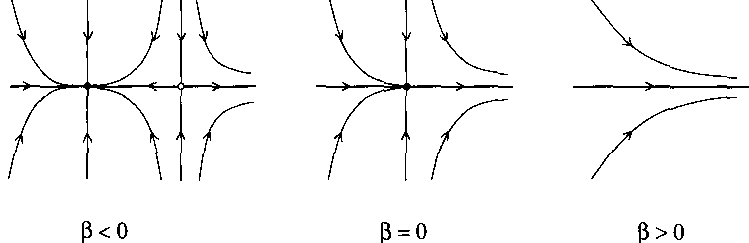
Figure: s110010a
Saddle-node (fold) bifurcation on the plane
The coefficient $ a $ can be computed (to within a scalar multiple) in terms of the right-hand sides of (a1), given two eigenvectors $ v,w \in \mathbf R ^ {n} $ corresponding to the zero eigenvalue of $ A $ and of its transpose $ A ^ {T} $, respectively:
$$ Av = A ^ {T} w = 0, \quad \left \langle {w,v } \right \rangle = 1, $$
where $ \langle {w,v } \rangle = \sum _ {i = 1 } ^ {n} w _ {i} v _ {i} $ is the inner product in $ \mathbf R ^ {n} $. Namely [a6],
$$ a = { \frac{1}{2} } \left . { \frac{d ^ {2} }{d \tau ^ {2} } } \left \langle {w,f ( \tau v,0 ) } \right \rangle \right | _ {\tau = 0 } . $$
For discrete-time dynamical systems, similar results are valid concerning bifurcations of fixed points with a simple eigenvalue $ \mu _ {1} = 1 $ of the Jacobian matrix [a2], [a8], [a6].
References
| [a1] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Theory of bifurcations of dynamical systems on a plane" , Israel Program Sci. Transl. (1971) (In Russian) |
| [a2] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Grundlehren math. Wiss. , 250 , Springer (1983) (In Russian) |
| [a3] | J. Carr, "Applications of center manifold theory" , Springer (1981) |
| [a4] | J. Guckenheimer, Ph. Holmes, "Nonlinear oscillations, dynamical systems and bifurcations of vector fields" , Springer (1983) MR0709768 Zbl 0515.34001 |
| [a5] | A. Kelley, "The stable, center stable, center, center unstable and unstable manifolds" J. Diff. Eq. , 3 (1967) pp. 546–570 MR0221044 |
| [a6] | Yu.A. Kuznetsov, "Elements of applied bifurcation theory" , Springer (1995) MR1344214 Zbl 0829.58029 |
| [a7] | A. Vanderbauwhede, "Centre manifolds, normal forms and elementary bifurcations" Dynamics Reported , 2 (1989) pp. 89–169 MR1000977 Zbl 0677.58001 |
| [a8] | D.C. Whitley, "Discrete dynamical systems in dimensions one and two" Bull. London Math. Soc. , 15 (1983) pp. 177–217 MR0697119 Zbl 0513.58033 |
Saddle-node bifurcation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Saddle-node_bifurcation&oldid=48601