Riemann-Roch theorem
A theorem expressing the Euler characteristic $ \chi ( {\mathcal E} ) $
of a locally free sheaf $ {\mathcal E} $
on an algebraic or analytic variety $ X $
in terms of the characteristic Chern classes of $ {\mathcal E} $
and $ X $ (cf. Chern class). It can be used to calculate the dimension of the space of sections of $ {\mathcal E} $ (the Riemann–Roch problem).
The classical Riemann–Roch theorem relates to the case of non-singular algebraic curves $ X $ and states that for any divisor $ D $ on $ X $,
$$ \tag{1 } l( D) - l( K _ {X} - D) = \mathop{\rm deg} D - g + 1, $$
where $ l( D) = \mathop{\rm dim} H ^ {0} ( X, {\mathcal O} _ {X} ( D)) $ is the dimension of the space of functions $ f \in k( x) $ for which $ ( f ) + D \geq 0 $, $ K _ {X} $ is the canonical divisor and $ g $ is the genus of $ X $. In the middle of the 19th century B. Riemann used analytic methods to obtain the inequality
$$ l( D) \geq \mathop{\rm deg} D - g + 1. $$
The equality (1) was proved by E. Roch.
The Riemann–Roch theorem for curves is the one-dimensional case of the more general Riemann–Roch–Hirzebruch–Grothendieck theorem. Let $ X $ be a non-singular projective variety of dimension $ n $, and let $ H ^ {. } X $ be an appropriate cohomology theory: either $ H ^ {. } X = H ^ {. } ( X, \mathbf Q ) $ are singular cohomology spaces when the basic field $ k = \mathbf C $, or $ H ^ {. } X = A( X) \otimes \mathbf Q $ where $ A( x) $ is a Chow ring, or $ H ^ {. } X $ is the ring associated to the Grothendieck ring $ K ^ {0} ( X) $ (see [2], [7]). Let $ {\mathcal E} $ be a locally free sheaf of rank $ r $ on $ X $. Universal polynomials for $ {\mathcal E} $ with rational coefficients, $ \mathop{\rm ch} (-) $ and $ \mathop{\rm td} (-) $, in the Chern classes $ c _ {i} ( {\mathcal E} ) \in H ^ {. } X $ of $ {\mathcal E} $ are defined in the following way. The factorization
$$ c _ {t} ( E) = c _ {0} ( {\mathcal E} ) + \dots + c _ {r} ( {\mathcal E} ) t ^ {r} = \ \prod _ { i= 1} ^ { r } ( 1 + a _ {i} t) $$
is examined for the Chern polynomial, where the $ a _ {i} $ are formal symbols. The exponential Chern character is defined by the formula
$$ \mathop{\rm ch} ( {\mathcal E} ) = \sum _ { i= 1} ^ { r } e ^ {a _ {i} } \ \left ( e ^ {x} = 1 + x + \frac{1}{2!} x ^ {2} + \dots \right ) , $$
and, accordingly, the Todd class is defined as
$$ \mathop{\rm td} ( {\mathcal E} ) = \prod _ { i= 1} ^ { r } \frac{a _ {i} }{1 - e ^ {- a _ {i} } } ; $$
$ \mathop{\rm ch} ( {\mathcal E} ) $ and $ \mathop{\rm td} ( {\mathcal E} ) $ are symmetric functions in the $ a _ {i} $ and they can be written as polynomials in $ c _ {i} ( {\mathcal E} ) $.
The Riemann–Roch–Hirzebruch theorem: If $ X $ is a non-singular projective variety or a compact complex variety of dimension $ n $ and if $ {\mathcal E} $ is a vector bundle of rank $ r $ on $ X $, then
$$ \chi ( {\mathcal E} ) = \mathop{\rm deg} ( \mathop{\rm ch} ( {\mathcal E} ) \mathop{\rm td} ( {\mathcal T} _ {X} )) _ {n} , $$
where $ {\mathcal T} _ {X} $ is the tangent sheaf on $ X $ and $ \mathop{\rm deg} ( \cdot ) _ {n} $ denotes the component of degree $ n $ in $ H ^ {. } X $. This theorem was proved by F. Hirzebruch in the case of the ground field $ \mathbf C $. When $ n = 2 $ and the invertible sheaf $ {\mathcal E} = {\mathcal O} _ {X} ( D) $, it leads to the equation
$$ \chi ( {\mathcal O} _ {X} ( D)) = \frac{1}{2} D( D - K _ {X} ) + \frac{1}{12} ( K _ {X} ^ {2} + c _ {2} ), $$
where $ c _ {2} = c _ {2} ( X) $ is the second Chern class of the surface $ X $ and $ K _ {X} $ is its canonical class. In particular, when $ D = 0 $ Noether's formula is obtained:
$$ \chi ( {\mathcal O} _ {X} ) = 1 + p _ {a} = \frac{1}{12} ( K _ {X} ^ {2} + c _ {2} ). $$
For three-dimensional varieties $ ( n= 3) $ the theorem leads to
$$ \chi ( {\mathcal O} _ {X} ( D)) = \frac{1}{6} D ^ {3} - \frac{1}{4} D ^ {2} K _ {X} + \frac{1}{12} D( K _ {X} ^ {2} + c _ {2} ) - \frac{1}{24} K _ {X} c _ {2} . $$
In particular, when $ D = 0 $,
$$ \chi ( {\mathcal O} _ {X} ) = - \frac{1}{24} K _ {X} c _ {2} . $$
In 1957, A. Grothendieck generalized the Riemann–Roch–Hirzebruch theorem to the case of a morphism of non-singular varieties over an arbitrary algebraically closed field (see [1]). Let $ K _ {0} X $ and $ K ^ {0} X $ be the Grothendieck groups of the coherent and locally free sheafs on $ X $, respectively (cf. Grothendieck group). The functor $ K _ {0} X $ is a covariant functor from the category of schemes and proper morphisms into the category of Abelian groups. In this case, for a proper morphism $ f: X \rightarrow Y $ the morphism $ f: K _ {0} X \rightarrow K _ {0} Y $ is defined by the formula
$$ f _ {!} ( {\mathcal F}) = \sum (- 1) ^ {i} R ^ {i} f _ {*} ( {\mathcal F} ), $$
where $ {\mathcal F} $ is an arbitrary coherent sheaf on $ X $ and $ K ^ {0} X $ is a covariant functor into the category of rings. For regular schemes with an ample sheaf, the groups $ K _ {0} X $ and $ K ^ {0} X $ coincide and are denoted by $ K( X) $. The Chern character $ \mathop{\rm ch} : K( X) \rightarrow H ^ {. } X $ is a homomorphism of rings; $ H ^ {. } X $ is also a covariant functor: The Gizin homomorphism $ f _ {*} : H ^ {. } X \rightarrow H ^ {. } Y $ is defined. When $ H ^ {. } X = H ^ {. } ( X, \mathbf Q ) $, the homomorphism $ f _ {*} $ is obtained from $ f _ {*} $ for homology spaces using Poincaré duality. The theorem as generalized by Grothendieck expresses the measure of deviation from commutativity of the homomorphisms $ f _ {!} $ and $ \mathop{\rm ch} $.
The Riemann–Roch–Hirzebruch–Grothendieck theorem: Let $ f : X \rightarrow Y $ be a smooth projective morphism of non-singular projective varieties; then for any $ x \in K( X) $ the equation
$$ \mathop{\rm ch} ( f _ {!} ( x)) = f _ {*} ( \mathop{\rm ch} ( x) \mathop{\rm td} ( {\mathcal T} _ {f} )) $$
in $ H ^ {. } X $ is true, where $ {\mathcal T} _ {f} = {\mathcal T} _ {X} - f ^ { * } ( {\mathcal T} _ {Y} ) \in K _ {X} $ (the relative tangent sheaf of the morphism $ f $).
When $ Y $ is a point, this theorem reduces to the Riemann–Roch–Hirzebruch theorem. There are generalizations (see [5], [6], [7]) when $ Y $ is a Noetherian scheme with an ample invertible sheaf, when $ f $ is a projective morphism whose fibres are locally complete intersections, and also to the case of singular quasi-projective varieties.
Several versions of the Riemann–Roch theorem are closely connected with the index problem for elliptic operators (see Index formulas). For example, the Riemann–Roch–Hirzebruch theorem for compact complex varieties is a particular case of the Atiyah–Singer index theorem.
References
| [1] | A. Borel, J.-P. Serre, "La théorème de Riemann–Roch" Bull. Soc. Math. France , 86 (1958) pp. 97–136 |
| [2] | Yu.I. Manin, "Lectures on the 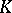 -functor in algebraic geometry" Russian Math. Surveys , 24 : 5 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 MR265355 -functor in algebraic geometry" Russian Math. Surveys , 24 : 5 (1969) pp. 1–89 Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 3–86 MR265355 |
| [3] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
| [4] | F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) MR1335917 MR0202713 Zbl 0376.14001 |
| [5] | P. Baum, W. Fulton, R. MacPherson, "Riemann–Roch for singular varieties" Publ. Math. IHES , 45 (1975) pp. 101–145 |
| [6] | P. Baum, W. Fulton, R. MacPherson, "Riemann–Roch for topological 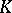 -theory and singular varieties" Acta Math. , 143 : 3–4 (1979) pp. 155–192 -theory and singular varieties" Acta Math. , 143 : 3–4 (1979) pp. 155–192 |
| [7] | "Théorie des intersections et théorème de Riemann–Roch" P. Berthelot (ed.) et al. (ed.) , Sem. Geom. Alg. 6 , Lect. notes in math. , 225 , Springer (1971) |
Comments
There are analogues of the Riemann–Roch theorem in algebraic number theory and arithmetic algebraic geometry.
References
| [a1] | S. Lang, "Algebraic number theory" , Addison-Wesley (1970) MR0282947 Zbl 0211.38404 |
| [a2] | K. Szpiro, "Sem. sur les pinceaux arithmétiques: La conjecture de Mordell" Astérisque , 127 (1985) |
Riemann–Roch theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann%E2%80%93Roch_theorem&oldid=22984