Representation of a Lie algebra
in a vector space $ V $
A homomorphism $ \rho $ of a Lie algebra $ L $ over a field $ k $ into the algebra $ \mathfrak g \mathfrak l ( V) $ of all linear transformations of $ V $ over $ k $. Two representations $ \rho _ {1} : L \rightarrow \mathfrak g \mathfrak l ( V _ {1} ) $ and $ \rho _ {2} : L \rightarrow \mathfrak g \mathfrak l ( V _ {2} ) $ are called equivalent (or isomorphic) if there is an isomorphism $ \alpha : V _ {1} \rightarrow V _ {2} $ for which
$$ \alpha ( \rho _ {1} ( l) v _ {1} ) = \ \rho _ {2} ( l) \alpha ( v _ {1} ) $$
for arbitrary $ l \in L $, $ v _ {1} \in V _ {1} $. A representation $ \rho $ in $ V $ is called finite-dimensional if $ \mathop{\rm dim} V < \infty $, and irreducible if there are no subspaces in $ V $, distinct from the null subspace and all of $ V $, that are invariant under all operators $ \rho ( l) $, $ l \in L $.
For given representations $ \rho _ {1} : L \rightarrow \mathfrak g \mathfrak l ( V _ {1} ) $ and $ \rho _ {2} : L \rightarrow \mathfrak g \mathfrak l ( V _ {2} ) $ one constructs the representations $ \rho _ {1} \oplus \rho _ {2} $( the direct sum) and $ \rho _ {1} \otimes \rho _ {2} $( the tensor product) of $ L $ into $ V _ {1} \oplus V _ {2} $ and $ V _ {1} \otimes V _ {2} $, by putting
$$ ( \rho _ {1} \oplus \rho _ {2} ) ( l) ( v _ {1} , v _ {2} ) = \ ( \rho _ {1} ( l) v _ {1} ,\ \rho _ {2} ( l) v _ {2} ), $$
$$ ( \rho _ {1} \otimes \rho _ {2} ) ( l) v _ {1} \otimes v _ {2} = \rho _ {1} ( l) v _ {1} \otimes v _ {2} + v _ {1} \otimes \rho _ {2} ( l) v _ {2} , $$
where $ v _ {1} \in V _ {1} $, $ v _ {2} \in V _ {2} $, $ l \in L $. If $ \rho $ is a representation of $ L $ in $ V $, then the formula
$$ \langle \rho ^ {*} ( l) u , v \rangle = - \langle u , \rho ( l) v \rangle $$
defines a representation $ \rho ^ {*} $ of $ L $ in the space dual to $ V $; it is called the contragredient representation with respect to $ \rho $.
Every representation of $ L $ can be uniquely extended to a representation of the universal enveloping algebra $ U ( L) $; this gives an isomorphism between the category of representations of $ L $ and the category of modules over $ U ( L) $. In particular, to a representation $ \rho $ of $ L $ corresponds the ideal $ \mathop{\rm ker} \widetilde \rho $ in $ U ( L) $— the kernel of the extension $ \widetilde \rho $. If $ \rho $ is irreducible, $ \mathop{\rm ker} \widetilde \rho $ is a primitive ideal. Conversely, every primitive ideal in $ U ( L) $ can be obtained in this manner from an (in general, non-unique) irreducible representation $ \rho $ of $ L $. The study of the space $ \mathop{\rm Prim} U ( L) $ of primitive ideals, endowed with the Jacobson topology, is an essential part of the representation theory of Lie algebras. It has been studied completely in case $ L $ is a finite-dimensional solvable algebra and $ k $ is an algebraically closed field of characteristic zero (cf. [2]).
Finite-dimensional representations of finite-dimensional Lie algebras over an algebraically closed field of characteristic zero have been studied most extensively [6], [3], [5]. When the field is $ \mathbf R $ or $ \mathbf C $, these representations are in one-to-one correspondence with the analytic finite-dimensional representations of the corresponding simply-connected (complex or real) Lie group. In this case every representation of a solvable Lie algebra contains a one-dimensional invariant subspace (cf. Lie theorem). Any representation of a semi-simple Lie algebra is totally reduced, i.e. is isomorphic to a direct sum of irreducible representations. The irreducible representations of a semi-simple Lie algebra have been completely classified: the classes of isomorphic representations correspond one-to-one to the dominant weights; here, a weight, i.e. an element of the dual space $ H ^ \star $ of a Cartan subalgebra $ H $ of $ L $, is called dominant if its values on a canonical basis $ h _ {1} \dots h _ {r} $ of $ H $ are non-negative integers (cf. Cartan theorem on the highest weight vector). For a description of the structure of an irreducible representation by its corresponding dominant weight (its highest weight) see Multiplicity of a weight; Character formula.
An arbitrary element (not necessarily a dominant weight) $ \lambda \in H ^ {*} $ also determines an irreducible linear representation of a semi-simple Lie algebra $ L $ with highest weight $ \lambda $. This representation is, however, infinite-dimensional (cf. Representation with a highest weight vector). The corresponding $ U ( L) $- modules are called Verma modules (cf. [2]). A complete classification of the irreducible infinite-dimensional representations of semi-simple Lie algebras has not yet been obtained (1991).
If $ k $ is an algebraically closed field of characteristic $ p > 0 $, then irreducible representations of a finite-dimensional Lie algebra $ L $ are always finite-dimensional and their dimensions are bounded by a constant depending on $ n = \mathop{\rm dim} L $. If the algebra $ L $ has a $ p $- structure (cf. Lie $ p $- algebra), then the constant is $ p ^ {( n - r)/2 } $, where $ r $ is the minimum possible dimension of an annihilator of a linear form on $ L $ in the co-adjoint representation [4]. The following construction is used for the description of the set of irreducible representations in this case. Let $ Z ( L) $ be the centre of $ U ( L) $ and let $ M _ {L} $ be the affine algebraic variety (of dimension $ \mathop{\rm dim} M _ {L} = n $) whose algebra of regular functions coincides with $ Z ( L) $( a Zassenhaus variety). The mapping $ \rho \mapsto \mathop{\rm ker} ( \rho \mid _ {Z( L) } ) $ makes it possible to assign a point on the Zassenhaus variety to each irreducible representation. The mapping thus obtained is surjective, the pre-image of any point of $ M _ {L} $ is finite and for the points of an open everywhere-dense subset this pre-image consists of one element [7]. A complete description of all irreducible representations has been obtained for nilpotent Lie algebras (cf. [8]) and certain individual examples (cf. [9], [10]). Most varied results have also been obtained for special types of representations.
References
| [1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [2] | J. Dixmier, "Enveloping algebras" , North-Holland (1977) (Translated from French) |
| [3] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [4] | A.A. Mil'ner, "Maximal degree of irreducible Lie algebra representations over a field of positive characteristic" Funct. Anal. Appl. , 14 : 2 (1980) pp. 136–137 Funkts. Anal. i Prilozhen. , 14 : 2 (1980) pp. 67–68 |
| [5] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [6] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Secr. Math. Univ. Paris (1955) |
| [7] | H. Zassenhaus, "The representations of Lie algebras of prime characteristic" Proc. Glasgow Math. Assoc. , 2 (1954) pp. 1–36 |
| [8] | B.Yu. Veisfeiler, V.G. Kats, "Irreducible representations of Lie 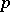 -algebras" Funct. Anal. Appl. , 5 : 2 (1971) pp. 111–117 Funkts. Anal. i Prilozhen. , 5 : 2 (1971) pp. 28–36 -algebras" Funct. Anal. Appl. , 5 : 2 (1971) pp. 111–117 Funkts. Anal. i Prilozhen. , 5 : 2 (1971) pp. 28–36 |
| [9] | J.C. Jantzen, "Zur Charakterformel gewisser Darstellungen halbeinfacher Gruppen und Lie-Algebren" Math. Z. , 140 : 1 (1974) pp. 127–149 |
| [10] | A.N. Rudakov, "On the representation of the classical Lie algebras in characteristic 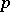 " Math. USSR Izv. , 4 (1970) pp. 741–749 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 4 (1970) pp. 735–743 " Math. USSR Izv. , 4 (1970) pp. 741–749 Izv. Akad. Nauk SSSR Ser. Mat. , 34 : 4 (1970) pp. 735–743 |
Comments
For a study of Prim $ U( L) $ for semi-simple $ L $, see [a2].
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) |
| [a2] | J.C. Jantzen, "Einhüllende Algebren halbeinfacher Lie-Algebren" , Springer (1983) |
Representation of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Representation_of_a_Lie_algebra&oldid=48518