Reliability and inspection of control systems
problems in the reliability of control systems
A branch of the theory of control systems that studies control systems subject to noise.
Let $ \mathfrak U = \{ U \} $ be a class of control systems and suppose there is a source of noise, or of faults, the effect of which on a control system $ U $ is to convert it into control systems $ U _ {1} \dots U _ {r} $ of some class $ \mathfrak U ^ \prime $. If it is assumed that the source of noise may also preserve the control system unchanged, e.g. $ U _ {1} = U $, then $ \mathfrak U \subseteq \mathfrak U ^ \prime $. Suppose that each control system in $ \mathfrak U ^ \prime $ is uniquely determined by its scheme $ \Sigma $; then the action of the source of noise reduces to its action on $ \Sigma $. A source of failures subjects the scheme to a transformation, manifested in one of the following ways: a) a disruption in the operation of the elements, i.e. changes in the elements; b) a change in the connections among the elements; etc. As a result, the original scheme $ \Sigma $ of $ U $ moves into "faulty" states $ \Sigma _ {1} \dots \Sigma _ {r} $, where $ \Sigma _ {1} = \Sigma $, defining control systems $ U _ {1} \dots U _ {r} $, respectively. Associated with these schemes one has corresponding functions $ \phi _ {1} \dots \phi _ {r} $, called failure functions (note that $ \phi _ {1} = \phi $ characterizes the performance of the original control system $ U $). The source of failure is usually characterized additionally either by an error-probability distribution or by restrictions on the possible number of elementary failures.
Reliability problems are considered mainly for three classes of control systems: diagrams of functional elements, contact schemes and automata (cf. Automaton; Contact scheme; Diagram of functional elements).
Let $ \mathfrak U $ be a class of diagrams of functional elements, the latter belonging to a given basis $ B $, where $ B = B _ {1} \cup B _ {2} $ and $ B _ {1} = \{ F _ {1} \dots F _ {s} \} $. If the failure source affects only the elements of the diagram, it converts elements $ F _ {i} $ in $ B _ {1} $, $ i = 1 \dots s $, into elements with the same number of inputs as $ F _ {i} $, but with a possibly different performance; the elements of $ B _ {2} $ remain unchanged. Thus, $ B _ {1} $ consists of unreliable elements and $ B _ {2} $ of reliable ones. In this case the source of failure can be described in terms of the failure probabilities $ p _ {1} \dots p _ {s} $ of the elements $ F _ {1} \dots F _ {s} $, respectively. For example, $ B _ {1} $ might consist of $ \mathop{\rm NO} $- elements, $ \textrm{ AND } $- elements and $ \mathop{\rm OR} $- elements, and $ B _ {2} $ of voting elements, implementing the functions $ \overline{x}\; $, $ x _ {1} $ and $ x _ {2} $, $ x _ {1} \lor x _ {2} $, and $ h ( x _ {1} , x _ {2} , x _ {3} ) = x _ {1} x _ {2} \lor x _ {1} x _ {3} \lor x _ {2} x _ {3} $, respectively. It may be assumed here that $ p _ {1} = p _ {2} = p _ {3} = p $ is the (common) failure probability of the elements of $ B _ {1} $.
When $ \mathfrak U $ is a class of contact schemes, one considers a failure source in which the elementary failures are either short-circuited or broken contacts. In this context one assumes in addition that in a contact scheme implementing functions of $ n $ variables there may occur at most $ m ( n) $ elementary failures.
The problems that arise in connection with the reliability and inspection of such systems may be divided into three types.
I. Design of reliable schemes of unreliable elements.
This branch of the theory has been developed for two classes of systems: contact schemes and diagrams of functional elements. For the latter, $ \Sigma $ is characterized by a certain probability $ p $ of cases in which it functions incorrectly. Here there are two basic questions.
1) What properties must the basis $ B $ have so that it should be possible, for any Boolean function $ f ( x _ {1} \dots x _ {n} ) $ and any $ \epsilon > 0 $, to design a diagram realizing $ f $ and such that the probability $ p $ of faulty performance be less than $ \epsilon $? In other words, it is desired that any Boolean function should be realizable by an arbitrarily reliable diagram.
It has been established that there are bases in which, for any function, there is an arbitrarily reliable diagram realizing it. An example is the basis $ B $( see above): $ B _ {1} $ consists of $ \mathop{\rm NO} $- elements, $ \textrm{ AND } $- elements and $ \mathop{\rm OR} $- elements with failure probability $ p < 1/3 $, and $ B _ {2} $ consists of an absolutely-reliable voting element. Necessary and sufficient conditions have been determined in terms of $ B $ under which arbitrarily reliable diagrams can be designed for all Boolean functions.
2) To devise a method for the synthesis of minimal (or in some sense almost minimal) diagrams realizing Boolean functions, of unreliability not exceeding a preassigned value $ \epsilon $. It turns out (e.g. for the above-described basis, with $ p < 1/9 $) that a method can be devised for synthesizing diagrams which, for the majority of Boolean functions and a given $ \epsilon $, yields asymptotically (in $ n $) minimal diagrams. In particular, for the Shannon function $ L ( n, \epsilon ) $, expressing the minimum number of elements in $ B $( see previous example) sufficient for the realization of any Boolean function of $ n $ variables with unreliability at most $ \epsilon $, one has the following asymptotic relationship:
$$ L ( n, \epsilon ) \sim \ { \frac{1}{2} } \frac{2 ^ {n} }{n} . $$
II. Design of self-correcting schemes.
This direction has been most thoroughly studied for two classes of systems — contact schemes and diagrams of functional elements. In this context the failure source is characterized by constraints on the number of elementary breakdowns. It is assumed that within the limits of the discussion no further changes occur in the scheme. A scheme $ \Sigma $ realizing a function $ \Phi $ is said to be self-correcting relative to a given failure source if $ \Phi _ {i} = \Phi $, $ i = 1 \dots r $. In other words, a self-correcting scheme functions correctly, regardless of the effect of the failure source. For example, the contact scheme of Fig. a, which realizes the function $ x _ {1} x _ {2} \lor x _ {1} x _ {3} \lor x _ {2} x _ {3} $, is self-correcting for a source that produces at most one broken contact.

Figure: r081170a
The major problems in this area are: 1) to clarify the conditions under which self-correcting schemes exist; and 2) to work out methods for the synthesis of minimal (or in some sense almost minimal) self-correcting schemes. Below the solution to these problems in the case of contact schemes with a failure source producing at most $ m ( n) $ short-circuited and broken contracts is given.
It turns out that for any Boolean function $ f ( x _ {1} \dots x _ {n} ) $ one can design a self-correcting scheme relative to this failure source. This can be done by taking any contact scheme $ \Sigma $ that realizes $ f $, replacing therein every contact $ x ^ \sigma $ by a subscheme consisting of $ m + 1 $ identical blocks connected in series, each of which consists of $ m + 1 $ copies of the given contact $ x ^ \sigma $ connected in parallel. This scheme is known as a trivial self-correcting scheme. Its complexity is $ ( m + 1) ^ {2} $ times that of the original scheme. The example of Fig. a shows that there also exist non-trivial self-correcting schemes.
The problem of designing self-correcting schemes is a special case of the synthesis problem for control systems with additional conditions. The main result here is that for most Boolean functions $ f ( x _ {1} \dots x _ {n} ) $ one can design a self-correcting scheme (relative to some class of sources) whose complexity asymptotically approaches (as $ n \rightarrow \infty $) the complexity of a minimal scheme realizing $ f $ but not being self-correcting. It has been shown that, subject to certain restrictions on the order of increase of $ m ( n) $, the Shannon function satisfies the following asymptotic relationship:
$$ L _ {m} ( n) \sim \ \frac{2 ^ {n} }{n} . $$
III. Inspection of control systems.
This area has been most thoroughly investigated for three classes of systems: contact schemes, diagrams of functional elements and automata. The consideration of inspection problems for control systems pre-supposes the following: 1) the presence of a failure source that, having affected the control system, maintains the latter in its failed state for some time, during which it produces no further failures; 2) a specification of the desired objective of the inspection; the latter is defined as the detection of some property of the control system. E.g., to determine whether the system is functioning correctly or not (checking problem), or, if the system has failed, to detect the source of the failure (diagnostics problem); and 3) a specification of the means of inspection. Inspection may be carried out with or without intervention in the scheme — for example, replacement of elements by standard elements, interchanging blocks of the same type, using additional check-points in the scheme, etc. The means of inspection also include some procedure for extracting information about the controlled object. These are experiments falling into two categories — unconditional and conditional. In unconditional experiments, the signal sequences fed to the input of the controlled device are pre-determined and are independent of the sequence at its output. In conditional experiments each successive symbol in the input sequence can be selected depending on the symbols appearing at the output at the previous instant of time.
A set of experiments that permits the detection of a given property is called a test. Since there are usually a great number of different tests detecting any desired property, one introduces a complexity measure in the set of tests and aims to find a test of minimum complexity. The main problem here is how to devise minimal or near-minimal tests for each property. This is part of a more general problem — the construction of compact algorithms for the recognition of various properties.
To illustrate this, consider the solution of these problems for contact schemes and diagrams of functional elements, assuming no interference in the scheme. The starting point here is the sequence of failure functions $ \Phi _ {1} \dots \Phi _ {r} $ of the scheme $ \Sigma $ realizing $ \Phi $, where $ \Phi _ {1} = \Phi $. It may happen that $ \Phi _ {i} = \Phi _ {j} $ for some pairs $ ( i, j) $, meaning that the $ i $- th and $ j $- th failures are indistinguishable. Thus, the set of functions $ \{ \Phi _ {i} \} $ is partitioned into equivalence classes $ \phi _ {1} \dots \phi _ {l} $ such that $ \Phi _ {i} $ and $ \Phi _ {j} $ belong to the same class if and only if $ \Phi _ {i} = \Phi _ {j} $; it is assumed that $ \Phi _ {1} $ is in the class $ \phi _ {1} $. Failures producing functions of the same class are indistinguishable. The classes $ \phi _ {1} \dots \phi _ {l} $ yield a table of failure functions.
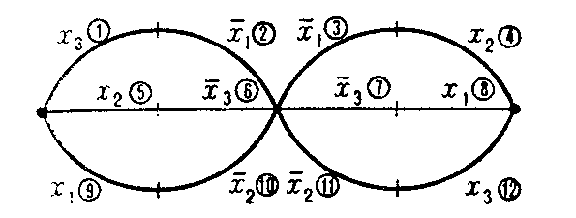
Figure: r081170b
Example. The contact scheme of Fig. bimplements the function
$$ \Phi = \ \overline{x}\; _ {1} x _ {2} x _ {3} \lor \overline{x}\; _ {1} \overline{x}\; _ {2} x _ {3} \lor \overline{x}\; _ {1} x _ {2} \overline{x}\; _ {3} \lor x _ {1} x _ {2} \overline{x}\; _ {3} \lor x _ {1} \overline{x}\; _ {2} \overline{x}\; _ {3} \lor x _ {1} \overline{x}\; _ {2} x _ {3} , $$
and the failure source produces at most one broken contact. Here $ \Phi _ {1} = \Phi _ {2} $, $ \Phi _ {3} = \Phi _ {4} $, $ \Phi _ {5} = \Phi _ {6} $, $ \Phi _ {7} = \Phi _ {8} $, $ \Phi _ {9} = \Phi _ {10} $, and $ \Phi _ {11} = \Phi _ {12} $. Thus there are seven classes: $ \phi _ {1} = \{ \Phi \} $, $ \phi _ {2} = \{ \Phi _ {1} , \Phi _ {2} \} \dots \phi _ {7} = \{ \Phi _ {11} , \Phi _ {12} \} $, generating the failure function table illustrated below. The property to be detected is usually specified in terms of a subset $ \mathfrak N $ of pairs $ ( i, j) $, denoting the indices of the classes of failure functions that one wishes to distinguish. For example, if $ \mathfrak N = \{ ( 1, i) \} $, $ i = 1 \dots l $, the property is distinguishability of the correctly-operating scheme from any failed stated (checking problem). If $ \mathfrak N = \{ ( i, j) \} $, $ i \neq j $, $ 1 \leq i, j \leq l $, one wishes to know how to distinguish each state from any other state (diagnostics problem). Finally, if $ \mathfrak N = \{ ( i, j) \} $, $ 1 \leq i \leq l _ {0} < j \leq l $,
one has the problem of "block" diagnostics, i.e. to identify the part of the scheme containing the failed element.
<tbody> </tbody>
|
Let $ \{ e _ {1} \dots e _ {k} \} $ be the set of sequences on which the functions $ \phi _ {1} \dots \phi _ {l} $ are defined. A set of sequences $ T = \{ e \} $ selected from $ \{ e _ {1} \dots e _ {k} \} $ is called a test for the given failure function table relative to the subset $ \mathfrak N $ if, for any pair $ ( i, j) $ in $ \mathfrak N $, there is a sequence $ e $ in $ T $ such that $ \phi _ {i} ( e) \neq \phi _ {j} ( e) $. A test $ T $ is said to be minimal if it contains the minimum possible number of sequences. A test is called a dead-end test if removal of any sequence $ e $ from $ T $ results in a subset of sequences that is not a test. The entire set $ \{ e _ {1} \dots e _ {k} \} $ is a (trivial) test. A minimal test is a dead-end test. The problem of finding a minimal test is motivated by the need to reduce the inspection time.
There exists an algorithm for the determination of all dead-end tests (hence also of minimal tests). Let $ \{ e _ {1} ^ {ij} \dots e _ {\nu ( i, j) } ^ {ij} \} $ be the set of all sequences on which $ \phi _ {i} $ and $ \phi _ {j} $ are different. Multiplying out in the expression
$$ \& _ {( i, j) \in \mathfrak R } ( e _ {1} ^ {ij} \lor \dots \lor e _ {\nu ( i, j) } ^ {ij} ) $$
according to the rules of Boolean algebra and then deleting "absorbed" terms by using the relation $ A \& B \lor A = A $, the remaining expression will correspond to a dead-end test. Thus, considering the above example, with regard to the checking problem
$$ \mathfrak R = \ \{ ( 1, 2), ( 1, 3) \dots ( 1, 7) \} , $$
the algorithm yields
$$ ( e _ {1} \lor e _ {2} ) \ ( e _ {2} \lor e _ {3} ) \ ( e _ {3} \lor e _ {4} ) \ ( e _ {4} \lor e _ {5} ) \ ( e _ {5} \lor e _ {6} ) \ ( e _ {6} \lor e _ {1} ) = $$
$$ = \ ( e _ {2} \lor e _ {1} e _ {3} ) ( e _ {4} \lor e _ {3} e _ {5} ) ( e _ {6} \lor e _ {1} e _ {5} ) = $$
$$ = \ e _ {1} e _ {3} e _ {5} \lor e _ {2} e _ {4} e _ {6} \lor e _ {1} e _ {2} e _ {4} e _ {5} \ \lor e _ {1} e _ {3} e _ {4} e _ {6} \lor e _ {2} e _ {3} e _ {5} e _ {6} . $$
There are five dead-end tests: $ T _ {1} = \{ e _ {1} , e _ {3} , e _ {5} \} $, $ T _ {2} = \{ e _ {2} , e _ {4} , e _ {6} \} $, $ T _ {3} = \{ e _ {1} , e _ {2} , e _ {4} , e _ {5} \} $, $ T _ {4} = \{ e _ {1} , e _ {3} , e _ {4} , e _ {6} \} $, $ T _ {5} = \{ e _ {2} , e _ {3} , e _ {5} , e _ {6} \} $; of these, $ T _ {1} $ and $ T _ {2} $ are minimal. This algorithm may be used to detect errors in the assembling of component elements. With slight modifications, it is also applicable to the design of short dead-end experiments for automata. Its efficiency drops sharply as the failure function table increases in size. To improve its efficiency one must take into consideration such factors as the structure of the table and further information as to the structure of the scheme itself. Several methods have been devised to this end. Other aspects of the reliability and inspection of control systems are elaborated in probability theory.
References
| [1] | I.A. Chegis, S.V. Yablonskii, "Logical means for controlling the functioning of electric systems" Trudy Mat. Inst. Steklov. , 51 (1958) pp. 270–360 (In Russian) |
| [2] | N.A. Solov'ev, "Tests" , Novosibirsk (1978) (In Russian) |
| [3] | Yu.G. Potapov, S.V. Yablonskii, "On the synthesis of self-correcting relay circuits" Soviet Phys. Dokl. , 5 (1961) pp. 932–935 Dokl. Akad. Nauk SSSR , 134 : 3 (1960) pp. 544–547 |
| [4] | J. von Neumann, "Probabilistic logics and the synthesis of reliable organisms from unreliable components" , Automata studies , Princeton Univ. Press (1956) pp. 43–98 |
| [5] | E.F. Moore, C.E. Shannon, "Reliable circuits using less reliable relays I, II" J. Franklin Inst. , 262 (1956) pp. 198–208; 281–297 |
Reliability and inspection of control systems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reliability_and_inspection_of_control_systems&oldid=48505