Racah-Wigner coefficients
The mathematical entities known as $ 3n - j $
coefficients enter mathematics and physics in describing the reduction of the $ ( n + 1 ) $-
fold Kronecker product of the unitary irreducible representations of the unitary unimodular group $ { \mathop{\rm SU}\nolimits} ( 2 ) $,
the group of $ ( 2 \times2 ) $
unitary unimodular matrices, into unitary irreducible representations of $ { \mathop{\rm SU}\nolimits} ( 2 ) $.
This reduction has the form:
$$ \tag{a1} C ^{T} [ D ^ {j _ 1} ( U ) \times \dots \times D ^ {j _{n} + 1} ( U ) ] C = $$
$$
=
\sum _{j} \oplus e _ {j _{1} \dots j} D ^{j} ( U ) ,
$$
where the symbols and quantities entering this relation have the following definitions:
1) $ D ^{j} ( U ) $ denotes the $ ( 2j + 1 ) $- dimensional unitary irreducible representation of $ { \mathop{\rm SU}\nolimits} ( 2 ) $ given explicitly below, where $ j \in \{ 1, {1 / 2} , {3 / 2} , \dots \} $, and this label is called an irreducible representation label or an angular momentum quantum number.
2) $ \times $ denotes the matrix direct product (Kronecker product), and $ n + 1 $ such products enter the left-hand side with arbitrary irreducible representation labels $ j _{1} \dots j _ {n+1} $.
3) $ \oplus $
denotes the matrix direct sum, and the direct sum on the right-hand side contains each irreducible representation $ D ^{j} ( U ) $
a number of times equal to
$$ \tag{a2} e _ {j _{1} \dots j _ {n + 1} j} = $$
$$
=
\sum _ {k _{1} ,k _{n} \dots k _ {n - 1}} e _ {j _{1} j _{2} k _ 1} e _ {k _{1} j _{3} k _ 2} e _ {k _{2} j _{4} k _ 3} \dots \dots e _ {k _ {n - 2} j _{n} k _ {n - 1}} e _ {k _ {n - 1} j _ {n + 1} j} ,
$$
in which $ j $
is any irreducible representation label given by
$$ \tag{a3} j = j _{1} + \dots + j _ {n + 1} , j _{1} + \dots + j _ {n + 1} - 1 \dots j _ {\textrm{ min }} ^ {n + 1} $$
(see below). For an arbitrary triple $ ( j _{a} ,j _{b} ,j _{c} ) $
of irreducible representation labels, the quantity $ e _ {j _{a} j _{b} j _ c} $
is $ 0 $
or $ 1 $,
and it is $ 1 $
if and only if the so-called triangle conditions are satisfied:
$$ \tag{a4} e _ {j _{a} j _{n} j _ c} = 1 $$
for $ j _{a} = j _{b} + j _{c} , j _{b} + j _{c} - 1 \dots | {j _{a} - j _ b} | $.
4) $ C $
denotes a real orthogonal matrix of dimension $ { \mathop{\rm dim}\nolimits} C = \prod _ {i =1} ^ {n + 1} ( 2j _{i} + 1 ) $,
with elements called Wigner–Clebsch–Gordan coefficients (WCG coefficients) for $ n = 1 $
and generalized Wigner–Clebsch–Gordan coefficients (generalized WCG coefficients) for $ n \geq 2 $.
5) The summation is over all $ j $
given by:
$$ \tag{a5} j = j _ {\textrm{ max }} ^ {( n + 1 )} , j _ {\textrm{ max }} ^ {( n + 1 )} - 1, j _ {\textrm{ max }} ^ {( n + 1 )} - 2 \dots j _ {\textrm{ min }} ^ {( n + 1 )} , $$
where $ j _ {\textrm{ max }} ^ {( k )} $
is given by:
$$ \tag{a6} j _ {\textrm{ max }} ^ {( k )} = j _{1} + \dots + j _{k} , \ k = 2,3 \dots $$
and the minimum value of $ j $
is determined recursively from
$$ \tag{a7} j _ {\textrm{ min }} ^ {( k + 1 )} = $$
$$
=
{ \mathop{\rm min}\nolimits} \left \{ {\left | {a - j _ {k + 1}} \right |} : {a = j _ {\textrm{ max }} ^ {( k )} , j _ {\textrm{ max }} ^ {( k )} - 1 \dots j _ {\textrm{ min }} ^ {( k )}} \right \} .
$$
The content of (a1) is completed by giving the explicit form of the unitary irreducible representations entering the direct product. These may be described as follows: Let $ k $
denote an arbitrary non-negative integer and let the pairs $ ( \alpha _{1} , \alpha _{2} ) $
and $ ( \beta _{1} , \beta _{2} ) $
consist of non-negative integers such that $ \alpha _{1} + \alpha _{2} = \beta _{1} + \beta _{2} = k $(
such pairs are called weights, or contents, of $ k $).
Introduce the homogeneous polynomials of degree $ k $
in the elements of an arbitrary $ ( 2 \times2 ) $-
matrix of indeterminates $ Z = ( z _ {ij} ) _ {1 \leq i,j \leq2} $
defined by:
$$ \tag{a8} P _ {\alpha, \beta} ^{k} ( Z ) = \sum _ {( \alpha;A; \beta )} \prod _ {i,j} { \frac{z _ {ij} ^ {a _ {ij}}}{a _ {ij} !} } , $$
where the summation is to be carried out over all $ ( 2 \times2 ) $-
matrices $ A = ( a _ {ij} ) _ {1 \leq i,j \leq2} $
of non-negative integers with row and column sums given by the weights $ \alpha $
and $ \beta $
of $ k $:
$$ \tag{a9}
\left \{
\begin{array}{c}
{ {a _ {11} + a _ {12} = \alpha _{1} ,} \\
{a _ {21} + a _ {22} = \alpha _{2} ,} \\
{a _ {11} + a _ {21} = \beta _{1} ,} \\
{a _ {12} + a _ {22} = \beta _{2} .}}
\end{array}
\right .
$$
Significant properties of the functions (a8) are:
transposition:
$$ \tag{a10} P ^{k} ( Z ^{T} ) = ( P ^{k} ( Z ) ) ^{T} , $$
where $ T $
denotes matrix transposition;
multiplication:
$$ \tag{a11} P ^{k} ( Z ^ \prime ) P ^{k} ( Z ) = P ^{k} ( Z ^ \prime Z ) ; $$
generation:
$$ \tag{a12} { \frac{\left ( \sum _ {i,j} x _{i} z _ {ij} y _{h} \right ) ^ k}{k!} } = \sum _ {\alpha, \beta} x _{1} ^ {\alpha _ 1} x _{2} ^ {\alpha _ 2} P _ {\alpha, \beta} ^{k} ( Z ) y _{1} ^ {\beta _ 1} y _{2} ^ {\beta _ 2} ; $$
orthogonality:
$$ \tag{a13} \left ( P _ {\alpha, \beta} ^{k} , P _ {\alpha ^ \prime , \beta ^ \prime} ^ {k ^ \prime} \right ) = k! { \frac{\delta _ {k,k ^ \prime} \delta _ {\alpha, \alpha ^ \prime} \delta _ {\beta, \beta ^ \prime}}{\prod _{i} \alpha _{i} ! \beta _{i} !} } ; $$
inner product:
$$ \tag{a14} ( P,P ^ \prime ) = {\overline{P}\;} \left ( { \frac \partial {\partial Z} } \right ) P ^ \prime ( Z ) | _ {Z = 0} , $$
where the bar denotes complex conjugation, $ P $
and $ P ^ \prime $
are arbitrary polynomials in the $ z _ {ij} $,
and
$$ { \frac \partial {\partial Z} } = \left ( { \frac \partial {\partial z _ {11}} } , { \frac \partial {\partial z _ {12}} } , { \frac \partial {\partial z _ {21}} } , { \frac \partial {\partial z _ {22}} } \right ) . $$
In the first two of these properties, $ P ^{k} ( Z ) $
denotes the $ k $-
dimensional matrix with rows and columns enumerated, respectively, by the weights $ \alpha $
and $ \beta $
as they assume all possible values for the given $ k $.
The unitary irreducible representation functions in (a1) are given in terms of the polynomials $ P _ {\alpha \beta} ^{k} ( Z ) $
by
$$ \tag{a15} D _ {m,m ^ \prime} ^{j} ( U ) = $$
$$
=
[ ( j + m ) ! ( j - m ) ! ( j + m ^ \prime ) ! ( j - m ^ \prime ) ! ] ^ {1/2} \times
$$
$$
\times
P _ {( j + m,j - m ) ( j + m ^ \prime , j - m ^ \prime )} ^ {2j + 1} ( U ) ;
$$
that is, by choosing $ k = 2j + 1 $,
$ \alpha _{1} = j + m $,
$ \alpha _{2} = j - m $,
$ \beta _{1} = j + m ^ \prime $,
$ \beta _{2} = j - m ^ \prime $,
so that $ j $
is any integer or half odd integer, and for each such $ j $
the so-called projection quantum numbers $ m $
and $ m ^ \prime $,
which are $ U ( 1 ) \subset { \mathop{\rm SU}\nolimits} ( 2 ) $
subgroup irreducible representation labels, assume the values $ j,j - 1 \dots - j $.
By convention, these values of $ m $
and $ m ^ \prime $
label the rows and columns of the $ ( 2j + 1 ) $-
dimensional unitary matrix $ D ^{j} ( U ) $.
(Conventionally, the rows are labelled from top to bottom by the greatest to the least value of $ m $,
and the columns are similarly labelled from left to right by $ m ^ \prime $).
Often, the irreducible representation functions (a15) are presented in a form in which $ U \in { \mathop{\rm SU}\nolimits} ( 2 ) $
is parametrized. A general way of doing this is to use the property that the $ ( 2 \times2 ) $
unitary modular matrices are in one-to-one correspondence with the points on the $ 3 $-
dimensional unit sphere $ S ^{3} $:
$$ \tag{a16}
U = \left (
\begin{array}{cc}
\alpha _{0} - i \alpha _{3} &- i \alpha _{1} - i \alpha _{2} \\
- i \alpha _{1} + i \alpha _{2} &\alpha _{0} + i \alpha _{3} \\
\end{array}
\right ) ,
$$
$$
\alpha _{0} ^{2} + \alpha _{1} ^{2} + \alpha _{2} ^{2} + \alpha _{3} ^{2} = 1.
$$
One can then parametrize the points $ ( \alpha _{0} , \alpha _{1} , \alpha _{2} , \alpha _{3} ) \in S ^{3} $
in any manner one chooses to obtain corresponding parametrizations of the representation functions.
The definitions and results given above are the basis relations underlying the origin of all $ 3n - j $ coefficients for all $ n = 1,2, \dots $. The general problem leads to beautiful results and unsolved problems involving labelled binary trees, Cayley trivalent trees, and cubic graphs. This subject cannot be developed here, but its flavour can be indicated by the special results for $ n = 1,2,3 $, which are presented in summary form below, focussing on these combinatorial aspects. The formulation of the $ 3n - j $ problem can also be given in a purely Lie algebra setting, where the general procedure is known as addition of $ n + 1 $ angular momenta.
There is an extensive literature on this subject. Classical references include [a1], [a25], [a26], [a2], [a3], [a4], [a5], [a6], [a7], [a8], [a9], [a10], [a11], [a12], [a13], [a14], [a15], [a16], [a17], [a18], with more recent work in [a19], [a20], [a21], [a22], [a23], [a24]. The notations in [a19], [a20] are followed.
Vector space constructions.
On assumes as given a vector space $ H _{j} $ with an inner product, denoted by $ \langle {} \mid {} \rangle $, where $ j $ is an arbitrary integer or half integer, $ 0, {1 / 2} ,1, {3 / 2} , \dots $. This vector space $ H _{j} $ also has an orthonormal basis given by the abstract ket vectors
$$ \tag{a17} B _{j} = \left \{ {\left | {jm} \right \rangle} : {m = j,j - 1 \dots - j} \right \} , $$
with an inner product
$$ \tag{a18} \left \langle {jm} \mid {jm ^ \prime} \right \rangle = \delta _ {mm ^ \prime} . $$
Spaces corresponding to distinct $ j $
are also to be perpendicular. Finally, there is an action $ T _{U} $,
for each $ U \in { \mathop{\rm SU}\nolimits} ( 2 ) $,
of the unitary group $ { \mathop{\rm SU}\nolimits} ( 2 ) $,
defined on $ H _{j} $
such that the action on the orthonormal basis $ B _{j} $
is given by:
$$ \tag{a19} T _{U} \left | {jm ^ \prime} \right \rangle = \sum _{m} D _ {mm ^ \prime} ^{j} ( U ) \left | {jm} \right \rangle . $$
It is the tensor product space $ H _ {j _{1} \dots j _ {n+1}} $
with orthonormal basis
$$ \tag{a20} B _ {j _{1} \dots j _ {n + 1}} = $$
$$
=
\left \{ {\left | {j _{1} m _ 1} \right \rangle \otimes \dots \otimes \left | {j _ {n + 1} m _ {n + 1}} \right \rangle} : {\forall m _{i} = j _{i} ,j _ {i - 1} \dots - j _ i} \right \}
$$
that underlies the $ ( n + 1 ) $-
fold Kronecker product in the left-hand side of (a1). The action of $ { \mathop{\rm SU}\nolimits} ( 2 ) $
on the space $ H _ {j _{1} \dots j _ {n+1}} $
is defined by its action on the basis (a17):
$$ {T _ U} : {H _ {j _{1} \dots j _ {n + 1}}} \rightarrow {H _ {j _{1} \dots j _ {n + 1}}} , $$
$$ \tag{a21}
T _{U} ( \left | {j _{1} m _{1} ^ \prime} \right \rangle \otimes \dots \otimes \left | {j _ {n + 1} m _ {n + 1} ^ \prime} \right \rangle ) =
$$
$$
=
T _{U} \left | {j _{1} m _{1} ^ \prime} \right \rangle \otimes \dots \otimes T _{U} \left | {j _ {n + 1} m _ {n + 1} ^ \prime} \right \rangle =
$$
$$
=
\sum _ {m _{1} \dots m _ {n + 1}} D _ {m _{1} m _{1} ^ \prime} ^ {j _ 1} ( U ) \dots D _ {m _ {n + 1} m _ {n + 1} ^ \prime} ^ {j _ {n + 1}} ( U ) \cdot
$$
$$
\cdot
\left | {j _{1} m _ 1} \right \rangle \otimes \dots \otimes \left | {j _ {n + 1} m _ {n + 1}} \right \rangle .
$$
Concrete realizations of these spaces are provided by the vectors defined by (a8) and (a15) with inner product (a14):
$$ \tag{a22} \left \langle Z \mid { {{j} \atop {m m ^ \prime}}} \right \rangle = ( 2j + 1 ) ^ {- {1 / 2}} D _ {m m ^ \prime} ^{j} ( Z ) , $$
which under left and right translations transform, in consequence of properties (a10) and (a11), as:
$$ \tag{a23} \left \langle {Z \mid L _ U} \mid { {{j} \atop {m m ^ \prime}}} \right \rangle = $$
$$
=
( 2j + 1 ) ^ {- {1 / 2}} D _ {m m ^ \prime} ^{j} ( U ^{T} Z ) =
$$
$$
=
\sum _ {m ^ {\prime \prime}} ^ j D _ {m ^ {\prime \prime} m} ^{j} ( U ) \left \langle Z \mid { {{j} \atop {m ^ {\prime \prime}m ^ \prime}}} \right \rangle ,
$$
$$ \tag{a24}
\left \langle {Z \mid R _ U} \mid { {{j} \atop {m m ^ \prime}}} \right \rangle =
$$
$$
=
( 2j + 1 ) ^ {- {1 / 2}} D _ {m m ^ \prime} ^{j} ( Z U ) =
$$
$$
=
\sum _ {m ^ {\prime \prime}} ^ j ( ZU ) D _ {m ^ {\prime \prime} m} ^{j} ( U ) \left \langle Z \mid { {{j} \atop {mm ^ {\prime \prime}}}} \right \rangle .
$$
$ 3 - j $coefficients.
Relation to Kronecker product.
$$ \tag{a25} D _ {m _{1} m _{1} ^ \prime} ^ {j _ 1} ( U ) D _ {m _{2} m _{2} ^ \prime} ^ {j _ 2} ( U ) = $$
$$
=
\sum _{j} C _ {m _{1} ,m _{2} ,m _{1} + m _ 2} ^ {j _{1} j _{2} j} C _ {m _{1} ^ \prime ,m _{2} ^ \prime , m _{1} ^ \prime + m _{2} ^ \prime} ^ {j _{1} j _{2} j} D _ {m _{1} + m _{2} ,m _{1} ^ \prime + m _{2} ^ \prime} ^{j} ( U ) ,
$$
where the $ C $-
coefficient is a WCG coefficient, which is an element of the real orthogonal matrix $ C $
of dimension $ ( 2j _{1} + 1 ) ( 2j _{2} + 1 ) $.
The coefficient has the properties
$$ \tag{a26} C _ {m _{1} m _{2} m} ^ {j _{1} j _{2} j} = 0 $$
unless $ j = j _{1} + j _{2} ,j _{1} + j _{2} -1 \dots | {j _{1} - j _ 2} | $;
$ m = m _{1} + m _{2} $.
These WCG coefficients satisfy the orthogonality relations
rows:
$$ \tag{a27} \sum _ {m _{1} + m _{2} = m} C _ {m _{1} m _{2} m} ^ {j _{1} j _{2} j} C _ {m _{1} m _{2} m} ^ {j _{1} j _{2} j ^ \prime} = \delta _ {j,j ^ \prime} ; $$
columns:
$$ \tag{a28} \sum _ {j,m} C _ {m _{1} m _{2} m} ^ {j _{1} j _{2} j} C _ {m _{1} ^ \prime m _{2} ^ \prime m} ^ {j _{1} j _{2} j} = \delta _ {m _{1} ,m _ 2} \delta _ {m _{1} ^ \prime ,m _{2} ^ \prime} . $$
Vector space properties.
Relation (a25) is valid when $ U $ is replaced by $ Z $. Using the inner product (a14) gives:
$$ \tag{a29} ( D _ {mm ^ \prime} ^{j} , D _ {m _{1} m _{1} ^ \prime} ^ {j _ 1} , D _ {m _{2} m _{2} ^ \prime} ^ {j _ 2} ) = ( 2j + 1 ) C _ {m _{1} m _{2} m} ^ {j _{1} j _{2} j} C _ {m _{1} ^ \prime m _{2} ^ \prime m ^ \prime} ^ {j _{1} j _{2} j} . $$
This relation (with a sign convention) may be used to calculate the WCG coefficients explicitly. One of the principal uses of the WCG coefficients in physical applications is the construction of a basis of the tensor product space $ H _ {j _{1} j 2} $
that transforms irreducibly under the action of $ { \mathop{\rm SU}\nolimits} ( 2 ) $:
$$ \tag{a30} = \sum _ {m _{1} ,m _ 2} C _ {m _{1} m _{2} m} ^ {j _{1} j _{2} j} \left | {j _{1} m _ 1} \right \rangle \otimes \left | {j _{1} m _ 1} \right \rangle , $$
$$ \tag{a31}
T _{U}
$$
$$ \sum _{m} D _ {mm ^ \prime} ^{j} ( U ) $$
A binary tree type of notation has been used to indicate the angular momentum coupling scheme.
Generating function.
J. Schwinger [a2] and T. Regge [a11] discovered the generating function for the WCG coefficients to be the power of a $ ( 3 \times3 ) $- determinant:
$$ \tag{a32} { \mathop{\rm det}\nolimits} \left ( \begin{array}{ccc} z _ {11} &z _ {12} &z _ {13} \\ z _ {21} &z _ {22} &z _ {23} \\ z _ {31} &z _ {32} &z _ {33} \\ \end{array} \right ) ^{k} = $$
$$
=
\sum _ {( k,k,k;A;k,k,k )} C _{k} ( A ) \prod _ {i,j = 1} ^ 3 ( z _ {ij} ) ^ {a _ {ij}} ,
$$
where the summation is carried out over all $ ( 3 \times3 ) $
magic square arrays $ A $
having row and column sums $ k $.
The coefficient $ C _{k} ( A ) $
is the restricted multinomial coefficient, given by
$$ \tag{a33} C _{k} ( A ) = \sum _ {k ( \pi ) : K = A} ( -1 ) ^ {k ( 132 ) + k ( 213 ) + k ( 321 )} \times $$
$$
\times
\left (
\begin{array}{c}
k \\
k ( 123 ) ,k ( 132 ) ,k ( 231 ) ,k ( 213 ) ,k ( 312 ) ,k ( 321 ) \\
\end{array}
\right ) ,
$$
where the summation is to be carried out over all $ k ( \pi ) $,
$ \pi \in S _{3} $,
such that the restriction $ K = A $
is met:
$$ \tag{a34} K = \left ( \begin{array}{ccc} k ( 123 ) + k ( 132 ) &k ( 213 ) + k ( 231 ) &k ( 312 ) + k ( 321 ) \\ k ( 213 ) + k ( 312 ) &k ( 321 ) + k ( 123 ) &k ( 132 ) + k ( 231 ) \\ k ( 321 ) + k ( 231 ) &k ( 132 ) + k ( 312 ) &k ( 123 ) + k ( 213 ) \\ \end{array} \right ) = $$
$$
=
A = \left (
\begin{array}{ccc}
a _ {11} &a _ {12} &a _ {13} \\
a _ {21} &a _ {22} &a _ {23} \\
a _ {31} &a _ {32} &a _ {33} \\
\end{array}
\right ) .
$$
Because of the restriction in the summation in (a33), the summation can be reduced (asymmetrically) to a sum with only one index.
The WCG coefficient is given by:
$$ \tag{a35} C _ {m _{1} m _{2} m} ^ {j _{1} j _{2} j} = $$
$$
=
\delta _ {m _{1} + m _{2} ,m} ( -1 ) ^ {j _{1} - j _{2} + m} \cdot
$$
$$
\cdot
\sqrt { {
\frac{( 2j + 1 ) \prod _ {ij} ( a _ {ij} ) !}{( j _{1} + j _{2} + j + 1 ) !}
}} \times {
\frac{C _ {j _{1} + j _{2} + j} ( A )}{( j _{1} + j _{2} + j ) !}
} ,
$$
$$
A = \left (
\begin{array}{ccc}
a _ {11} &a _ {12} &a _ {13} \\
a _ {21} &a _ {22} &a _ {23} \\
a _ {31} &a _ {32} &a _ {33} \\
\end{array}
\right ) =
$$
$$
=
\left (
\begin{array}{ccc}
j _{1} + m _{1} &j _{2} + m _{2} &j - m \\
j _{1} - m _{1} &j _{2} - m _{2} &j + m \\
j _{2} + j - j _{1} &j + j _{1} - j _{2} &j _{1} + j _{2} - j \\
\end{array}
\right ) .
$$
Symmetries.
It follows directly from the generating function that the $ 3 - j $ coefficient, which is defined by
$$ \tag{a36} \left ( \begin{array}{ccc} j _{1} &j _{2} &j _{3} \\ m _{1} &m _{2} &m _{3} \\ \end{array} \right ) = $$
$$
=
( 2j _{3} + 1 ) ^ {- {1 / 2}} ( -1 ) ^ {j _{1} + m _{1} - ( j _{2} - m _{2} )} C _ {m _{1} ,m _{2} , - m _ 3} ^ {j _{1} j _{2} j _ 3} ,
$$
has the $ 72 $
determinantal symmetries associated with row interchange, column interchange, and transposition of the $ ( 3 \times3 ) $-
determinant of $ Z $
between the parentheses, which transfer directly to the array $ A $.
The $ 3 - j $
coefficient is either invariant or changes its sign under the transformations of the $ ( j _{1} ,m _{1} ,j _{2} ,m _{2} ,j,m ) $
induced by the following transformations of the array $ A $:
invariance under even permutations of the rows or columns of $ A $,
and under transposition: multiplication by $ ( -1 ) ^ {j _{1} +j _{2} +j _ 3} $
under odd permutations of the rows or columns.
Binary coupling theory.
In the physics literature, the phrase "binary coupling theory" addresses the problem of reducing the multiple Kronecker product (a1) by repeatedly using the reduction result (a25) for two angular momenta. One encounters immediately the problem of how to associate pairs in multiple Kronecker products. For example, for $ n = 2 $, there are two such associations:
$$ \tag{a37} ( ( D ^ {j _ 1} \times D ^ {j _ 2} ) \times D ^ {j _ 3} ) , \ ( D ^ {j _ 1} \times ( D ^ {j _ 2} \times D ^ {j _ 3} ) ) , $$
For $ n = 3 $,
there are five such associations:
$$ \tag{a38} ( ( D ^ {j _ 1} \times D ^ {j _ 2} ) \times ( D ^ {j _ 3} \times D ^ {j _ 4} ) ) , $$
$$
( D ^ {j _ 1} \times ( ( D ^ {j _ 2} \times D ^ {j _ 3} ) \times D ^ {j _ 4} ) ) , ( D ^ {j _ 1} \times ( D ^ {j _ 2} \times ( D ^ {j _ 3} \times D ^ {j _ 4} ) ) ) ,
$$
$$
( ( D ^ {j _ 1} \times ( D ^ {j _ 2} \times D ^ {j _ 3} ) ) \times D ^ {j _ 4} ) , ( ( ( D ^ {j _ 1} \times D ^ {j _ 2} ) \times D ^ {j _ 3} ) \times D ^ {j _ 4} ) .
$$
In addition, all permutations of the irreducible representation labels $ ( j _{1} ,j _{2} \dots j _ {n+1} ) $
must be considered. Entire textbooks ([a14], [a17], [a22]) have been devoted to this subject, which leads to the representation of $ 3n - j $
coefficients by pairs of labelled binary trees and cubic graphs ([a20], p. 435). Some limited aspects of this subject are presented here in the context of the $ 6 - j $
and $ 9 - j $
coefficients.
An important topic, but one that is only partially developed, is that of generating functions for the $ 3n - j $ coefficients. The property of a $ 3n - j $ coefficient that characterizes its presentation in terms of a pair of labelled binary trees or in terms of a cubic graph is the set of angular momentum triangles associated with it. This number is always $ 2n $, the number of vertices in the associated cubic graph. A key concept for the generating function of a $ 3n - j $ coefficient is that of a triangle monomial. These monomials are defined as follows: Let $ ( z _{a} ,z _{b} ,z _{c} ) $ denote three distinct indeterminates and $ ( j _{a} ,j _{b} ,j _{c} ) $ three angular momentum quantum numbers constituting a triangle. The triangle monomial associated with these symbols is defined by
$$ \tag{a39} ( z _{a} ,z _{b} ,z _{c} ) ^ {( j _{a} ,j _{b} ,j _{c} )} = z _{a} ^ {j _{b} + j _{c} - j _ a} z _{b} ^ {j _{c} + j _{a} - j _ b} z _{c} ^ {j _{a} + j _{b} - j _ c} . $$
Let $ \Delta $
denote the set of triangles associated with a given $ 3n - j $
coefficient. The triangle monomial for this $ 3n - j $
coefficient is defined as
$$ \tag{a40} Z ^ \Delta = \prod _ {\textrm{ all \ triangles } \in \Delta} ( z _{a} ,z _{b} ,z _{c} ) ^ {( j _{a} ,j _{b} ,j _{c} )} . $$
The indeterminates $ ( z _{a} ,z _{b} ,z _{c} ) $
are coordinates associated with each of the $ 2n $
points of the cubic graph corresponding to the $ 3n - j $
coefficient. This is illustrated concretely below for the $ 6 - j $
and $ 9 - j $
coefficients.
It must be pointed out that $ 3n - j $ coefficients for $ n \geq 2 $ are qualitatively different objects than $ 3 - j $ coefficients. The vector space $ H _ {j _{1} \dots j _ {n+1}} $ with basis (a20) is the carrier space of the reducible representation of $ { \mathop{\rm SU}\nolimits} ( 2 ) $ given by the $ ( n + 1 ) $- fold Kronecker product in (a1). This space, which is of dimension
$$ \tag{a41} { \mathop{\rm dim}\nolimits} H _ {j _{1} \dots j _ {n + 1}} = \prod _ {i = 1} ^ {n + 1} ( 2j _{i} + 1 ) = \sum _{j} e _ {j _{1} \dots j _ {n + 1}} ( 2j + 1 ) , $$
may be written as a direct sum of $ e _ {j _{1} \dots j _ {n+1} j} $
perpendicular vector subspaces:
$$ \tag{a42} H _ {j _{1} \dots j _ {n + 1}} = \sum _ {\kappa = 1} ^ {e _ {j _{1} \dots j _ {n + 1}}} H _ {j _{1} \dots j _ {n + 1} j} ( \kappa ) . $$
Each subspace $ H _ {j _{1} \dots j _ {n+1} j} $
is of dimension $ 2j + 1 $
and has a basis of the form (a17) that transforms under the action of $ { \mathop{\rm SU}\nolimits} ( 2 ) $
in the standard way given by (a19). The $ 3n - j $
coefficients ( $ n \geq 2 $)
are elements of real orthogonal matrices that transform between certain pairs of these subspaces that arise in binary coupling theory, and these coefficients, taken collectively, provide the transformation between all such pairs of subspaces. The $ 3 - j $
coefficients provide a single such space, as a first step in the construction of the pairs in the binary coupling method.
One of the consequences of this qualitative difference is that no generating function for a $ 3n - j $ coefficient ( $ n \geq 2 $) is a power of a determinant. It is known for the $ 6 - j $ and $ 9 - j $ coefficients ([a2], [a15], [a16], [a21]) that these coefficients have generating functions that can be presented in the following uniform manner [a22]: There exists a polynomial $ C _ {2n} ( x,y ) $ with integer coefficients associated with the cubic graph corresponding to a $ 3n - j $ coefficient such that
$$ \tag{a43} { \frac{1}{[ 1 + C _ {2n} ( x,y ) ] ^ 2} } = \sum _ \Delta C _ {2n} ( \Delta ) Z ^ \Delta , $$
$$ \tag{a44}
( 3n - j ) \ \textrm{ coefficient } =
$$
$$
=
\left [ \prod _ {\textrm{ all \ triangles } \in \Delta} \{ j _{a} ,j _{b} ,j _{c} \} \right ] \times C _ {2n} ( \Delta ) ,
$$
where the symbol $ \{ j _{a} j _{b} j _{c} \} $
denotes the so-called triangle coefficient, defined by
$$ \tag{a45} \{ j _{a} ,j _{b} ,j _{c} \} = $$
$$
=
\left [ {
\frac{( j _{a} + j _{b} - j _{c} ) ! ( j _{b} + j _{c} - j _{a} ) ! ( j _{c} + j _{a} - j _{b} ) !}{( j _{a} + j _{b} + j _{c} + 1 ) !}
} \right ] ^ { {1 / 2}} .
$$
$ 6 - j $coefficients.
Relation to the Kronecker product.
The coefficients defined by
$$ \tag{a46} C _ {m _{1} ,m _{2} ,m _{1} + m _{2} ,m _{3} ,m} ^ {j _{1} j _{2} k _{1} j _{3} j} = C _ {m _{1} ,m _{2} ,m _{1} + m _ 2} ^ {j _{1} j _{2} k _ 1} C _ {m _{1} + m _{2} ,m _{3} ,m} ^ {k _{1} j _{3} j} $$
are elements of the orthogonal matrix $ C $
for $ n = 2 $
in (a1) that completely reduces the Kronecker product in the first coupling scheme given in (a37).
Vector space interpretation.
$$ \tag{a47} =\sum _ {m _{1} + m _{2} + m _{3} = m} C _ {m _{1} ,m _{2} ,m _{1} + m _ 2} ^ {j _{1} j _{2} k _ 1} C _ {m _{1} + m _{2} ,m _{3} ,m} ^ {k _{1} j _{3} j} \cdot $$
$$
\cdot
\left | {j _{1} m _ 1} \right \rangle \otimes \left | {j _{2} m _ 2} \right \rangle \otimes \left | {j _{3} m _ 3} \right \rangle ,
$$
$$ \tag{a48} =\sum _ {m _{1} ,m _ 2} C _ {m _{1} ,m _{2} ,m _{1} + m _ 2} ^ {j _{1} j _{2} k _ 1} C _ {m _{1} + m _{2} ,m - m _{1} - m _{2} ,m} ^ {k _{1} j _{3} j} \cdot $$
$$
\cdot
C _ {m _{2} ,m - m _{1} - m _{2} ,m - m _ 1} ^ {j _{2} j _{3} k _{1} ^ \prime} C _ {m - m _{1} ,m _{1} ,m} ^ {k _{1} ^ \prime j _{1} j} =
$$
$$
=
\sqrt {( 2k _{1} + 1 ) ( 2k _{1} ^ \prime + 1 )} W ( j _{1} j _{2} jj _{3} ;k _{1} k _{1} ^ \prime ) ,
$$
where the $ W $
coefficient is called a Racah coefficient. In fact, one could take (a48) as the definition of the Racah coefficient. It is independent of the $ m $
quantum number; that is, it is a $ U ( 1 ) \subset { \mathop{\rm SU}\nolimits} ( 2 ) $
invariant. All other non-trivial binary couplings of three angular momenta lead again to Racah coefficients, up to sign. For $ n = 2 $
there is only one invariant, the Racah coefficient.
It was a great feat of G. Racah [a25], [a26] (see also [a9], p. 162) to reduce the summation over four WCG coefficients in (a48), each of which is itself a summation over multinomial coefficients, to an expression involving but a single summation index. In the Wigner $ 6 - j $ notation, Racah's result is given by:
$$ \tag{a49} \left \{ \begin{array}{ccc} a & b & e \\ d & c & f \\ \end{array} \right \} ( -1 ) ^ {a + b + c + d} W ( abcd;ef ) = $$
$$
=
\{ abe \} \{ cde \} \{ acf \} \{ bdf \} \times
$$
$$
\times
\sum _{k} ( -1 ) ^{k} ( k + 1 ) \cdot
$$
$$
\cdot
\left (
\begin{array}{c}
k \\
k - v _{1} , k - v _{2} , k - v _{3} , k - v _{4} , e _{1} - k, e _{2} - k, e _{3} - k \\
\end{array}
\right ) .
$$
The triangles in the $ 6 - j $(
Racah) coefficient are $ ( abe ) $,
$ ( cde ) $,
$ ( acf ) $,
$ ( bdf ) $,
as inherited from the WCG coefficients in (a48), and $ \{ abe \} $,
$ \{ cde \} $,
$ \{ acf \} $,
$ \{ bdf \} $
denote the triangle coefficients defined in (a45). The quantities $ v _{i} $
and $ e _{j} $
are the discrete vertex and edge functions associated with the tetrahedron:
$$ \tag{a50} v _{1} = a + b + e, \ v _{2} = c + d + e, $$
$$
v _{3} = a + c + f, \ v _{4} = b + d + f, e _{1} = ( b + c ) + ( e + f ) , \ e _{2} = ( a + d ) + ( e + f ) ,
$$
$$
e _{3} = ( a + d ) + ( b + c ) .
$$
See (a55), in which the following identifications are to be made:
$$ \tag{a51} x _{1} = y _{1} = j _{1} = a, \ x _{2} = y _{2} = j _{2} = b, $$
$$
x _{3} = y _{3} = j _{3} = e, x _{4} = y _{4} = j _{4} = d,
$$
$$
x _{5} = y _{5} = j _{5} = c, \ x _{6} = y _{6} = j _{6} = f.
$$
The $ 6 - j $
coefficient (now using $ j _{i} $
labels throughout) labelled as
$$ \tag{a52} \left \{ \begin{array}{ccc} j _{1} &j _{2} &j _{3} \\ j _{4} &j _{5} &j _{6} \\ \end{array} \right \} $$
has four triangles, which are conveniently presented as the columns of a $ ( 3 \times4 ) $-
array:
$$ \tag{a53} \Delta = \left [ \begin{array}{cccc} j _{1} &j _{3} &j _{1} &j _{2} \\ j _{2} &j _{4} &j _{5} &j _{4} \\ j _{3} &j _{5} &j _{6} &j _{6} \\ \end{array} \right ] . $$
Generating function.
For the description of the generating function, the real coordinates
$$ \tag{a54} x = ( x _{1} ,x _{2} ,x _{3} ,x _{4} ,x _{5} ,x _{6} ) , $$
$$
y = ( y _{1} ,y _{2} ,y _{3} ,y _{4} ,y _{5} ,y _{6} )
$$
are introduced, and these are displayed, analogously to (a53) in a $ ( 3 \times4 ) $-
array, the columns of which are interpreted as the vertices, in Cartesian $ 3 $-
dimensional space $ \mathbf R ^{3} $,
of a tetrahedron:
$$ \tag{a55} Z = \left [ \begin{array}{cccc} x _{1} &y _{3} &y _{1} &y _{2} \\ x _{2} &x _{4} &y _{5} &y _{4} \\ x _{3} &x _{5} &x _{6} &y _{6} \\ \end{array} \right ] \rightarrow $$
The array of triangles $ \Delta $ in (a53) is obtained from the $ ( x,y ) $ by setting $ x _{i} = y _{i} = j _{i} $.
The generating function of the $ 6 - j $
coefficients is now obtained from the labelled tetrahedron in (a55) by the following rules. The function $ C _{4} ( x,y ) $
on the left-hand side of (a43) is given as follows. Interchange the $ x $
and $ y $
symbols. Then form
the vertex function:
$$ V _{3} ( x,y ) = y _{1} y _{2} y _{3} + x _{3} y _{4} y _{5} + x _{1} x _{5} y _{6} + x _{2} x _{4} x _{6} , $$
the edge function:
$$ \tag{a56} E _{4} ( x,y ) = x _{1} y _{1} x _{4} y _{4} + x _{2} y _{2} x _{5} y _{5} + x _{3} y _{3} x _{6} y _{6} , $$
the tetrahedral function:
$$ C _{4} ( x,y ) = V _{3} ( x,y ) + E _{4} ( x,y ) . $$
Using the tetrahedral function $ C _{4} ( x,y ) = V _{3} ( x,y ) + E _{4} ( x,y ) $
in the general form (a43) for $ n = 2 $
gives the $ 6 - j $
with the labels (a52), where the variables in a given triangle monomial (a40) with exponents given by the columns of $ \Delta $
in (a53) are those in the corresponding columns of the array $ Z $
on the left hand side of (a55).
Symmetries.
The symmetries of the $ 6 - j $ coefficients may be verified directly from the explicit form (a49), or from the generating function. For the coefficient written in the form
$$ \tag{a57} \left \{ \begin{array}{ccc} a & b & e \\ d & c & f \\ \end{array} \right \} , $$
the symmetries are best expressed in terms of the Bargmann $ ( 3 \times4 ) $-
array
$$ \tag{a58} \left [ \begin{array}{cccc} d + f - b &a + f - c &d + e - c &a + e - b \\ c + f - a &b + f - d &b + e - a &c + e - d \\ c + d - e &a + b - e &b + d - f &a + c - f \\ \end{array} \right ] , $$
as follows: The coefficient (a57) is invariant under all transformations of $ ( a,b,c,d,e,f ) $
induced by row or column permutations of the Bargmann array. This gives $ 144 $
symmetry relations, some simple substitutions, and other simple linear transformations.
$ 9 - j $coefficients.
Relation to the Kronecker product.
The coefficients defined by
$$ \tag{a59} C _ {m _{1} ,m _{2} , \sum _{1} ^ 2 m _{i} ,m _{3} , \sum _{1} ^ 3 m _{i} ,m _{4} ,m} ^ {j _{1} j _{2} k _{1} j _{3} k _{2} j _{4} j} = $$
$$
=
C _ {m _{1} ,m _{2} , \sum _{1} ^ 2 m _{i} , \sum _{1} ^ 2 m _{i} ,m _{2} , \sum _{1} ^ 3 m _ i} ^ {j _{1} j _{2} k _{1} k _{1} j _{3} k _ 2} C _ {\sum _{1} ^ 3 m _{i} ,m _{4} ,m} ^ {k _{2} j _{4} j}
$$
are the elements of the orthogonal matrix $ C $
for $ n = 3 $
in (a1) that completely reduces the Kronecker product in the bottom binary coupling scheme given in (a38).
Vector space interpretation.
$$ \tag{a60} =\sum _ {\sum _{1} ^ 4 m _ {ik} = m} C _ {m _{1} ,m _{2} , \sum _{1} ^ 2 m _{i} ,m _{3} , \sum _{1} ^ 3 m _{i} ,m _{4} ,m} ^ {j _{1} j _{2} k _{1} j _{3} k _{2} j _{4} j} \times $$
$$
\times
\left | {j _{1} m _ 1} \right \rangle \otimes \left | {j _{2} m _ 2} \right \rangle \otimes \left | {j _{3} m _ 3} \right \rangle \otimes \left | {j _{4} m _ 4} \right \rangle ;
$$
$$ \tag{a61} = ( - 1 ) ^ {k _{2} - k _{2} ^ \prime + j _{4} - j _ 1} \cdot $$
$$
\cdot
\left [ ( 2k _{1} + 1 ) ( 2k _{2} + 1 ) ( 2k _{1} ^ \prime + 1 ) ( 2k _{2} ^ \prime + 1 ) \right ] ^ { {1 / 2}} \cdot
$$
$$
\cdot
\left \{
\begin{array}{ccc}
j _{1} &j _{2} &k _{1} \\
k _{2} ^ \prime &k _{1} ^ \prime &j _{3} \\
j &j _{4} &k _{2} \\
\end{array}
\right \} .
$$
The bracket object is Wigner's notation for the $ 9 - j $
coefficient, and this relation (a61) may be taken as its definition. The summation over six WCG coefficients coming from the inner product in (a61), using (a60), may be reduced to the following summation over $ 6 - j $
coefficients (a switch to a $ j _{i} $
notation has been made):
$$ \tag{a62} \left \{ \begin{array}{ccc} j _{1} &j _{2} &j _{3} \\ j _{9} &j _{8} &j _{4} \\ j _{7} &j _{6} &j _{5} \\ \end{array} \right \} = \sum _{k} ( -1 ) ^ {2k} ( 2k + 1 ) \times $$
$$
\times
\left \{
\begin{array}{ccc}
j _{1} &j _{9} &j _{7} \\
j _{6} &j _{5} & k \\
\end{array}
\right \} \left \{
\begin{array}{ccc}
j _{2} &j _{8} &j _{6} \\
j _{9} & k &j _{4} , \\
\end{array}
\right \} \left \{
\begin{array}{ccc}
j _{3} &j _{4} &j _{5} \\
k &j _{1} &j _{2} \\
\end{array}
\right \} .
$$
The six triangles in a $ 9 - j $
coefficient are inherited from its expression in terms of WCG coefficients, or, equivalently, from the triangles in the $ 6 - j $
coefficients in (a62) not involving the summation index. It is convenient to display these six triangles as the columns in a $ ( 3 \times6 ) $-
array:
$$ \tag{a63} \Delta = \left [ \begin{array}{cccccc} j _{1} &j _{3} &j _{5} &j _{6} &j _{8} &j _{9} \\ j _{2} &j _{4} &j _{6} &j _{2} &j _{4} &j _{1} \\ j _{3} &j _{5} &j _{7} &j _{8} &j _{9} &j _{7} \\ \end{array} \right ] . $$
Generating function.
For the description of the generating function, the real coordinates
$$ \tag{a64} x = ( x _{1} \dots x _{9} ) , \ y = ( y _{1} \dots y _{9} ) $$
are introduced, and these are displayed, analogously to (a63), in a $ ( 3 \times6 ) $-
array, the columns of which are interpreted as the vertices, in Cartesian $ 3 $-
dimensional space, $ \mathbf R ^{3} $,
of a cubic graph on six vertices:
$$ \tag{a65} Z = \left [ \begin{array}{cccccc} x _{1} &y _{3} &y _{5} &y _{6} &y _{8} &y _{9} \\ x _{2} &x _{4} &x _{6} &y _{2} &y _{4} &y _{1} \\ x _{3} &x _{5} &x _{7} &x _{8} &x _{9} &x _{7} \\ \end{array} \right ] \rightarrow $$
The array of triangles $ \Delta $ in (a63) is obtained from the $ ( x,y ) $ in $ Z $ by setting $ x _{i} = y _{i} = j _{i} $. The generating function of the $ 9 - j $ coefficients is now obtained from the labelled cubic graph by the following rules. The function $ C _{6} ( x,y ) $ in the left hand side of (a43) is obtained as follows. Interchange the $ x $ and $ y $ symbols. Then form
the vertex function:
$$ \tag{a66} V _{4} ( x,y ) = x _{1} x _{4} x _{7} x _{8} + x _{1} x _{5} x _{9} y _{6} + x _{2} x _{4} x _{6} y _{9} + $$
$$
+
x _{2} x _{5} x _{8} y _{7} + x _{3} x _{8} y _{5} y _{9} + x _{6} x _{8} y _{1} y _{3} +
$$
$$
+
x _{7} x _{9} y _{2} y _{3} + x _{3} y _{4} y _{6} y _{7} + y _{1} y _{2} y _{4} y _{5} ;
$$
the edge function:
$$ \tag{a67} E _{6} ( x,y ) = { \mathop{\rm det}\nolimits} \left ( \begin{array}{ccc} x _{1} y _{1} &x _{2} y _{2} &x _{3} y _{3} \\ x _{4} y _{4} &x _{5} y _{5} &x _{6} y _{6} \\ x _{7} y _{7} &x _{8} y _{8} &x _{9} y _{9} \\ \end{array} \right ) ; $$
the six point cubic graph function:
$$ \tag{a68} C _{6} ( x,y ) = - V _{4} ( x,y ) + E _{6} ( x,y ) . $$
Using the function $ C _{6} ( x,y ) = - V _{4} ( x,y ) + E _{6} ( x,y ) $
in the general form (a43) for $ n = 3 $
gives the $ 9 - j $
coefficient with the labels (a62), where the variables in a given triangle monomial (a40) with exponents given by the columns of $ \Delta $
in (a63) are those in the corresponding columns of the array $ Z $
on the left hand side of (a65).
Symmetries.
The $ 9 - j $ coefficient has $ 72 $( known) symmetries, and these are just those originating from the $ 72 $ symmetries of the six $ 3 - j $ coefficients implicit on the left hand side of (a61). In terms of the coefficient written in the form (a62), these symmetries are expressed by: The $ 9 - j $ coefficient (a62) is invariant under even permutations of its rows or columns, under transposition of the array, and is multiplied by the factor $ ( - 1 ) ^ {\sum _{1} ^{9} j _ i} $ under odd permutations of its rows or columns.
Concluding remarks.
A great deal of work has been done on the relationship between cubic graphs and $ 3n - j $ coefficients, and the results can not even be surveyed here. It is important to point out, however, that for $ n = 3 $ there is a second non-isomorphic cubic graph on six vertices, the prism, or wedge, which leads to a simple product (with dimensional factors) of two $ 6 - j $ coefficients. While this is important for transforming between the relevant coupling schemes, it does not lead to a new $ 9 - j $ coefficient. Indeed, it can be proved that every $ 3n - j $ coefficient is a sum over products of $ 6 - j $ coefficients, and sometimes this sum may degenerate to a product of $ 3n ^ \prime - j $ coefficients ( $ n ^ \prime < n $), in which case it is not counted as new. For $ n \geq 4 $ there are always fewer "new" $ 3n - j $ coefficients than non-isomorphic cubic graphs. The general problem of the relation between $ 3n - j $ coefficients and non-isomorphic cubic graphs of $ 2n $ vertices is unsolved.
Relevant to the classification of $ 3n - j $ coefficients, indeed, for the definition of what the term "classification" means, are three basic relations:
triangle transformation:
$$ \tag{a69} { \frac{1}{\{ acf \} \{ bdf \}} } = ( 2f + 1 ) \sum _{e} { \frac{W ( abcd;ef )}{\{ abe \} \{ cde \}} } . $$
Racah sum rule:
$$ \tag{a70} \sum _{f} ( -1 ) ^ {b + d - f} W ( abcd;ef ) W ( adcb;gf ) = $$
$$
=
( -1 ) ^ {e + g - a - c} W ( bacd;eg ) .
$$
Biedenharn–Elliot identity, [a4], [a5]:
$$ \tag{a71} W ( a ^ \prime ab ^ \prime b;c ^ \prime e ) W ( a ^ \prime ed ^ \prime d;b ^ \prime c ) = $$
$$
=
\sum _{f} ( 2f + 1 ) \cdot
$$
$$
\cdot
W ( abcd;ef ) W ( c ^ \prime bd ^ \prime d;b ^ \prime f ) W ( a ^ \prime ad ^ \prime f;c ^ \prime c ) .
$$
Each of these relations has an interpretation in terms of fundamental operations in mathematics: The triangle transformation rule is a consequence of the associativity of three symplecton polynomials, which are polynomials of the form $ P _ {jm} $
over the four non-commuting variables $ x,y, {\partial / {\partial x}} , {\partial / {\partial y}} $(
or, equivalently, over two bosons and their conjugates) which transform irreducibly under a well-defined commutation action of $ { \mathop{\rm SU}\nolimits} ( 2 ) $.
Racah's sum rule has an interpretation in terms of the commutativity of a diagram associated with the coupling of three angular momenta. The Biedenharn–Elliot identity is a consequence of the associative law for three unit tensor operators. For a discussion of each of these results, see [a20], pp. 243; 453; 30.
References
| [a1] | E.P. Wigner, "On the matrices which reduce the Kronecker products of representation of S.R. groups" L.C. Biedenharn (ed.) H. van Dam (ed.) , Quantum Theory of Angular Momentum , Acad. Press (1965) pp. 87–133 (Original: 1940 (unpublished)) |
| [a2] | J. Schwinger, "On angular momentum" L.C. Bidenharn (ed.) H. van Dam (ed.) , Quantum Theory of Angular Momentum , Acad. Press (1965) pp. 229–279 (Original: U.S. Atomic Energy Commission Reports NYO–3071, 1952 (unpublished)) |
| [a3] | L.C. Biedenharn, J.M. Blatt, M.E. Rose, "Some properties of the Racah and associated coefficients" Rev. Mod. Phys. , 24 (1952) pp. 249–257 |
| [a4] | L.C. Biedenharn, "An identity satisfied by Racah coefficients" J. Math. Phys. , 31 (1953) pp. 287–293 |
| [a5] | J.P. Elliot, "Theoretical studies in nuclear spectroscopy. V: The matrix elements of non-central forces with an application to the  -shell" Proc. Roy. Soc. A , 218 (1953) pp. 345–370 -shell" Proc. Roy. Soc. A , 218 (1953) pp. 345–370 |
| [a6] | H.A. Jahn, J. Hope, "Symmetry properties of the Wigner 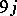 symbol" Phys. Rev. , 93 (1954) pp. 318–321 symbol" Phys. Rev. , 93 (1954) pp. 318–321 |
| [a7] | A. Arima, H. Horie, Y. Tanabe, "Generalized Racah coefficient and its application" Progress Theor. Phys. (Kyoto) , 11 (1954) pp. 143–154 |
| [a8] | A.R. Edmonds, "Angular momentum in quantum mechanics" , Princeton Univ. Press (1957) |
| [a9] | M.E. Rose, "Elementary theory of angular momentum" , Wiley (1957) |
| [a10] | U. Fano, G. Racah, "Irreducible tensorial sets" , Acad. Press (1959) |
| [a11] | T. Regge, "Symmetry properties of Clebsch–Gordan coefficients" Nuovo Cim. , 10 (1958) pp. 544–545 |
| [a12] | T. Regge, "Symmetry properties of Racah's coefficients" Nuovo Cim. , 11 (1959) pp. 116–117 |
| [a13] | W.T. Sharp, "Racah algebra and the contraction of groups" , Thesis Princeton Univ. Press (1960) |
| [a14] | A.P. Yutsis (Jucys), I.B. Levinson, V.V. Vanagas, "Mathematical apparatus of the theory of angular momentum" , Gordon&Breach (1964) (In Russian) |
| [a15] | V. Bargmann, "On the representations of the rotation group" Rev. Mod. Phys. , 345 (1962) pp. 829–845 |
| [a16] | A.C.T. Wu, "Structure of the Wigner 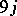 coefficients in the Bargmann approach" J. Math. Phys. , 13 (1972) pp. 84–90 coefficients in the Bargmann approach" J. Math. Phys. , 13 (1972) pp. 84–90 |
| [a17] | D.A. Varshalovich, A.N. Moskalev, V.K. Khersonskii, "Quantum theory of angular momentum" , Nauka (1975) (In Russian) |
| [a18] | A.P. Yutsis (Jucys), A.A. Bandzaitis, "Angular momentum theory in quantum mechanics" , Molslas , Vilnius (1977) (In Russian) |
| [a19] | L.C. Biedenharn, J.D. Louck, "Angular momentum in quantum physics" , Encycl. Math. Sci. , 8 , Cambridge Univ. Press (1981) |
| [a20] | L.C. Biedenharn, J.D. Louck, "The Racah–Wigner algebra in quantum theory" , Encycl. Math. Sci. , 9 , Cambridge Univ. Press (1981) |
| [a21] | B.R. Judd, G.M.S. Lister, "A class of generalized 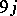 coefficients for coefficients for 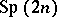 " J. Phys. A: Math. Gen. , 20 (1986) pp. 3159–3169 " J. Phys. A: Math. Gen. , 20 (1986) pp. 3159–3169 |
| [a22] | L.C. Biedenharn, W.Y.C. Chen, M.A. Lohe, J.D. Louck, "The role of 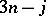 coefficients in coefficients in 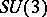 " T. Lulek (ed.) W. Florek (ed.) S. Walcerz (ed.) , Proc. 3rd SSCPM , World Sci. (1995) pp. 150–182 " T. Lulek (ed.) W. Florek (ed.) S. Walcerz (ed.) , Proc. 3rd SSCPM , World Sci. (1995) pp. 150–182 |
| [a23] | M. Danos, "??" , ?? (199?) |
| [a24] | J.D. Louck, "Unitary symmetry, combinatorics and generating functions" J. Discrete Math. , ?? (199?) |
| [a25] | G. Racah, "Theory of complex spectra. II" Phys. Rev. , 62 (1942) pp. 438–462 |
| [a26] | G. Racah, "Theory of complex spectra. III" Phys. Rev. , 63 (1943) pp. 367–382 |
Racah-Wigner coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Racah-Wigner_coefficients&oldid=44342