Quadrangle
In elementary geometry a quadrangle is a figure consisting of four segments intersecting in four (corner) points.
Figure: q076000a
Note that each point is incident with 2 lines, each line is incident with 2 points, that there is at most one line passing through two distinct points, that two lines intersect in at most one point, and that for a point and a line not incident with that point there is a unique line through that point intersecting the given line.
These properties exemplify the simplest case of a generalized quadrangle. This is an incidence system $ ( P, B, I) $, i.e. a (symmetric) incidence relation $ I \subset P \times B $ between points (the set $ P $) and lines (or blocks, the set $ B $) such that
i) for each point $ M $ and line $ p $ not passing through $ M $ there is precisely one pair $ ( N, n) $ with $ M $ on $ n $, $ N $ on $ n $ and $ p $.
A generalized quadrangle can be seen as a very special kind of bipartite graph (cf. Graph, bipartite), obtained by taking as its vertex set the disjoint union $ P\amalg B $ and with $ M \in P $, $ m \in B $ connected if and only if $ M $ is on $ m $.
Interchanging $ P $ and $ B $ one obtains the dual generalized quadrangle.
A generalized quadrangle is non-degenerate if there is no point that is collinear with all others, where two points are collinear if they are on a common line.
A finite generalized quadrangle of order $ ( s, t) $ is one that satisfies i) above and also
ii) each point is incident with precisely $ t + 1 $ lines and there is at most one line through two distinct points;
iii) each line has $ s+ 1 $ points and two lines intersect in at most one point.
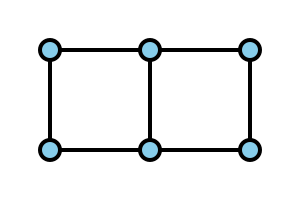
A simple example of a finite generalized quadrangle of order $(1, 2)$ is depicted below
This is also an example of a grid, which is an incidence structure $ ( P, B, I ) $ with $ P = \{ {x _ {ij} } : {i= 1 \dots s _ {1} , j = 1 \dots s _ {2} } \} $, $ B = \{ l _ {1} \dots l _ {s _ {1} } ; m _ {1} \dots m _ {s _ {2} } \} $ with $ x _ {ij} $ on $ l _ {k} $ if and only if $ i = k $ and $ x _ {ij} $ on $ m _ {k} $ if and only if $ j = k $.
There are three known families of generalized quadrangles associated with the classical groups; these are known as classical generalized quadrangles. There are also others, for instance coming from ovoids (cf. Ovoid).
Generalized quadrangles were introduced by J. Tits [a1] and he also described the classical ones and the first non-classical ones. More generally one considers generalized $ m $- gons, [a4].
References
| [a1] | J. Tits, "Sur la trialité et certain groupes qui s'en déduisent" Publ. Math. IHES , 2 (1959) pp. 14–60 |
| [a2] | R. Dembowski, "Finite geometries" , Springer (1968) pp. 254 |
| [a3] | S.E. Payne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984) |
| [a4] | E.E. Shult, "Characterizations of the Lie incidence geometries" K. Lloyd (ed.) , Surveys in Combinatorics , Cambridge Univ. Press (1983) pp. 157–186 |
Quadrangle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quadrangle&oldid=52705