Persian curve
From Encyclopedia of Mathematics
spiric curve
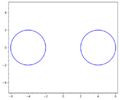
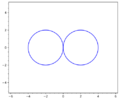
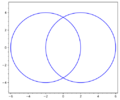
A plane algebraic curve of order four that is the line of intersection between the surface of a torus and a plane parallel to its axis (see Figures). The equation in rectangular coordinates is
$$(x^2+y^2+p^2+d^2-r^2)^2=4d^2(x^2+p^2),$$
where $r$ is the radius of the circle describing the torus, $d$ is the distance from the origin to its centre and $p$ is the distance from the axis of the torus to the plane. The following are Persian curves: the Booth lemniscate, the Cassini oval and the Bernoulli lemniscate.
The name is after the Ancient Greek geometer Persei (2nd century B.C.), who examined it in relation to research on various ways of specifying curves.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | F. Gomez Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
| [a2] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
How to Cite This Entry:
Persian curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Persian_curve&oldid=54377
Persian curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Persian_curve&oldid=54377
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article