Non-Euclidean geometries
In the literal sense — all geometric systems distinct from Euclidean geometry; usually, however, the term "non-Euclidean geometries" is reserved for geometric systems (distinct from Euclidean geometry) in which the motion of figures is defined, and this with the same degree of freedom as in Euclidean geometry. The degree of freedom of motion of figures in the Euclidean plane is characterized by the condition that every figure can be moved, without changing the distances between its points, in such a way that any selected point of the figure can be made to occupy a previously-designated position; moreover, every figure can be rotated about any of its points. In the Euclidean three-dimensional space every figure can be moved in such a way that any selected point of the figure will occupy any prescribed position; in addition, every figure can be rotated about any axis through any of its points.
The major non-Euclidean geometries are hyperbolic geometry or Lobachevskii geometry and elliptic geometry or Riemann geometry — it is usually these that are meant by "non-Euclidean geometries" . Hyperbolic geometry was the first geometric system distinct from Euclidean geometry, and the first more general theory (it includes Euclidean geometry as a limiting case). The later-discovered elliptic geometry is in some respects the opposite of hyperbolic geometry. The simultaneous investigation of the three geometries has made it possible to reveal the special features of each to a considerable degree and also to determine their relationships with other geometric systems. Below, both non-Euclidean geometries and Euclidean geometry will be compared, first as synthetic theories, then in the context of differential geometry and, lastly, in the context of group theory.
Non-Euclidean geometries as synthetic theories.
Hyperbolic geometry is based on the same axioms as Euclidean geometry, with the exception of the parallelism axiom. Recall that according to the latter, through any point not lying on a given straight line $ a $ there passes exactly one straight line coplanar with $ a $ which does not intersect it; in hyperbolic geometry it is assumed that there are several such lines (and it can then be proved that there are infinitely many).
The axiom adopted in elliptic geometry is: Every straight line coplanar with another straight line intersects the latter. This axiom contradicts the system of axioms of Euclidean geometry with the parallelism axiom excluded. Thus, the axiom system underlying elliptic geometry must be different from that of Euclidean geometry not only in the replacement of one axiom — the parallelism axiom — but also in part of the other axioms. The relevant axioms of these geometries in which the differences occur are those that determine the order relations among the geometric elements. Namely, in Euclidean and hyperbolic geometries, the order of the points on a straight line is linear, i.e. similar to the order in the set of real numbers; in elliptic geometry, the points of a straight line are cyclically ordered, like the points on a circle. In addition, in Euclidean and hyperbolic geometries every straight line in a given plane divides the plane into two parts; in elliptic geometry this is not true, i.e. any two points of the plane not on a given straight line can be joined within the plane by a continuous curve that does not cut the straight line (the topological model of the elliptic plane is the projective plane).
The axioms that determine the motion of figures are the same in all three geometries.
Examples of theorems in non-Euclidean geometries.
1) In hyperbolic geometry, the sum of the interior angles of any triangle is less than two right angles; in elliptic geometry it is larger than two right angles (in Euclidean geometry it is of course equal to two right angles).
2) In hyperbolic geometry, the area of a triangle is given by the formula
$$ \tag{1 } S = R ^ {2} ( \pi - \alpha - \beta - \gamma ), $$
where $ \alpha , \beta , \gamma $ are the interior angles of the triangle and $ R $ is a constant that depends on the specific unit chosen for the measurement of areas. In elliptic geometry, as well as in spherical geometry,
$$ \tag{2 } S = R ^ {2} ( \alpha + \beta + \gamma - \pi ) $$
with the same notation (in Euclidean geometry there is no fixed relationship between the area of a triangle and the sum of its angles).
3) In hyperbolic geometry there are various relations among the sides of a triangle and its angles, such as
$$ \tag{3 } \cosh { \frac{a}{R} } = \ \cosh { \frac{b}{R} } \cosh { \frac{c}{R} } - \ \sinh { \frac{b}{R} } \sinh { \frac{c}{R} } \ \cos \alpha , $$
where sinh, cosh denote the hyperbolic sine and cosine, $ a, b, c $ the sides of the triangle, $ \alpha , \beta , \gamma $ the angles opposite them, respectively, and $ R $ a constant depending on the choice of scale; for a right-angled triangle (with hypotenuse $ c $ and right angle $ \gamma $) one has, for example,
$$ \tag{4 } \cosh { \frac{c}{R} } = \ \mathop{\rm cotan} \alpha \mathop{\rm cotan} \beta . $$
Subject to a certain adjustment between the linear scale and the unit of area, the constant $ R $ in the formulas (1), (3) and (4) is the same. The number $ R $ is known as the radius of curvature of the hyperbolic plane (or space). For a given linear scale, $ R $ expresses the length of a certain segment in the hyperbolic plane (space), which is also called the radius of curvature. If the radius of curvature itself is chosen as the unit of length, then $ R = 1 $. In elliptic geometry, as in spherical trigonometry, there are similar formulas:
$$ \tag{5 } \cos { \frac{a}{R} } = \ \cos { \frac{b}{R} } \cos { \frac{c}{R} } + \ \sin { \frac{b}{R} } \sin { \frac{c}{R} } \ \cos \alpha $$
(for an arbitrary triangle) and
$$ \tag{6 } \cos { \frac{c}{R} } = \mathop{\rm cotan} \alpha \mathop{\rm cotan} \ \beta $$
(for a right-angled triangle) with analogous notation. The number $ R $ is called the radius of curvature of the elliptic plane (or space). As is evident from formulas (4) and (6), in each of the non-Euclidean geometries the hypotenuse of a right-angled triangle is determined by its angles; moreover, the sides of any triangle are determined by its angles, implying that there exist no similar triangles that are not congruent (in Euclidean geometry there are no analogues of formulas (4) and (6), and there exist no other formulas expressing linear quantities in terms of angular ones). Replacement of $ R $ by $ iR $ converts the formulas (1), (3), (4) into (2), (5), (6), respectively; in general, replacement of $ R $ by $ iR $ transforms all metric formulas of hyperbolic geometry into the corresponding formulas of elliptic geometry, while preserving their geometric meanings. As $ R \rightarrow \infty $, both systems yield formulas of Euclidean geometry (or become meaningless). Now this indefinite increase in $ R $ means that the scaling segment becomes infinitely small in comparison with the radius of curvature (as a segment). The fact that the formulas of non-Euclidean geometries tend in the limit to formulas of Euclidean geometry implies that, in non-Euclidean figures that are small in comparison with the radius of curvature, the relations between their elements differ only slightly from the Euclidean relations.
Non-Euclidean geometries in a differential-geometric context.
In each of the non-Euclidean geometries, the differential properties of the plane are analogous to those of surfaces in Euclidean space. To be specific: In a non-Euclidean plane one can introduce intrinsic coordinates $ u , v $ so that the differential $ ds $ of arc length of the curve corresponding to the differentials $ du, dv $ of the coordinates is defined by
$$ \tag{7 } ds ^ {2} = E du ^ {2} + 2 F du dv + G dv ^ {2} . $$
Suppose, in particular, that the coordinate $ u $ of an arbitrary point $ M $ is defined as the length of the perpendicular dropped from $ M $ to a fixed straight line, and the coordinate $ v $ as the distance from a fixed point 0 on the line to the base of the perpendicular; the signs of $ u $ and $ v $ are chosen as in the case of ordinary Cartesian coordinates. Then formula (7) becomes, for the hyperbolic plane,
$$ \tag{8 } ds ^ {2} = du ^ {2} + \cosh ^ {2} \left ( { \frac{u}{R} } \right ) dv ^ {2} , $$
and for the elliptic plane,
$$ \tag{9 } ds ^ {2} = \ du ^ {2} + \cos ^ {2} \left ( { \frac{u}{R} } \right ) dv ^ {2} , $$
$ R $ being the same constant as in the preceding section (the radius of curvature). The terms on the right of (8) and (9) are the metric forms of surfaces of constant curvature in Euclidean space — of negative curvature $ K = - 1/R ^ {2} $ in the first case (e.g. a pseudo-sphere) and of positive curvature $ K = 1/R ^ {2} $ in the second (e.g. a sphere). For this reason, the intrinsic geometry on a sufficiently small part of the hyperbolic plane coincides with the intrinsic geometry on the corresponding part of a surface of constant negative curvature. Similarly, the intrinsic geometry of sufficiently small parts of the elliptic plane is realized on surfaces of constant positive curvature (there are no surfaces in Euclidean space that realize the geometry of the whole hyperbolic plane). Replacement of $ R $ by $ iR $ converts the metric form (8) into the metric form (9).
Since the metric form determines the intrinsic geometry of the surface, the same transformation also converts other metric relationships of hyperbolic geometry into metric relationships of elliptic geometry (as already stated previously). If $ R = \infty $, each of (8) and (9) yields
$$ ds ^ {2} = du ^ {2} + dv ^ {2} , $$
which is simply the metric form of the Euclidean plane.
In regard to their differential properties, three-dimensional non-Euclidean spaces belong to the class of Riemannian spaces, being defined in that class primarily by the fact that they have constant Riemannian curvature. In both two and three dimensions, constant curvature guarantees that the space is homogeneous, i.e. that motion of figures is locally possible (and with the same degree of freedom as in the Euclidean plane or space, respectively). A hyperbolic space is of negative curvature $ - 1/R ^ {2} $, and an elliptic space is of positive curvature $ 1/R ^ {2} $( $ R $ is the radius of curvature). Euclidean space occupies an intermediate position: it is a space of curvature zero.
Spaces of constant Riemannian curvature can exhibit a great variety of topological structures. Among all spaces of constant negative curvature, a hyperbolic space is uniquely determined by two properties: it is complete (in the sense of completeness of a metric space) and topologically equivalent to ordinary Euclidean space. An elliptic space is uniquely determined in the class of all spaces of constant positive curvature by one property: topological equivalence to a projective space. Analogous conditions define hyperbolic and elliptic spaces of higher dimension in the class of higher-dimensional spaces of constant Riemannian curvature.
Non-Euclidean geometries in a group-theoretic context.
Consider the projective plane, with projective homogeneous coordinates $ ( x _ {1} , x _ {2} , x _ {3} ) $, and suppose that some second-order oval curve, henceforward denoted by $ k $, is given, say
$$ x _ {1} ^ {2} + x _ {2} ^ {2} - x _ {3} ^ {2} = 0. $$
Every projective mapping of the projective plane onto itself that leaves the curve $ k $ invariant is called an automorphism relative to $ k $. Every automorphism maps interior points of $ k $ to interior points. The set of all automorphisms relative to the curve $ k $ is a group. One considers only points of the projective plane lying within $ k $; chords of $ k $ will be called "straight lines" . Two figures will be considered equal if one of them can be transformed into the other by some automorphism. Since the automorphisms form a group, the fundamental properties of equality between figures are valid: 1) if a figure $ A $ equals a figure $ B $, then $ B $ equals $ A $; and 2) if $ A $ equals $ B $ and $ B $ equals $ C $, then $ A $ equals $ C $. In the geometric theory obtained in this way, all the axioms of Euclidean geometry are valid, except the parallelism axiom; instead, this geometry satisfies the hyperbolic axiom of parallelism (see Fig., which demonstrates that through a point $ P $ infinitely many "straight lines" can be drawn that do not intersect the "straight line" $ a $).
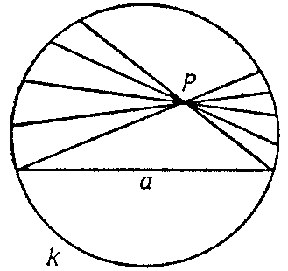
Figure: n067020a
The construction just outlined yields an interpretation of (two-dimensional) hyperbolic geometry in terms of a projective plane or, as is usually said, a projective model of hyperbolic geometry; the curve $ k $ is known as the absolute of the model. Automorphisms relative to $ k $ play the role of motions. For this reason, hyperbolic geometry can be regarded as a theory that studies the properties of figures and the related magnitudes that remain invariant under certain automorphisms; in brief, hyperbolic geometry is essentially the theory of invariants of an automorphism group relative to an absolute oval.
Elliptic geometry (in two dimensions) admits a similar interpretation; it is the theory of invariants relative to the imaginary absolute
$$ \tag{10 } x _ {1} ^ {2} + x _ {2} ^ {2} + x _ {3} ^ {2} = 0. $$
The points and straight lines of the model are all the points and straight lines of the projective plane, the automorphisms are defined in exclusively algebraic terms as linear transformations that transform equation (10) into an equation of the same form.
Euclidean geometry may also be considered as a theory of invariants of a certain group of projective transformations: the group of automorphisms relative to the degenerate absolute
$$ x _ {1} ^ {2} + x _ {2} ^ {2} = 0,\ x _ {3} = 0, $$
i.e. relative to the imaginary points $ ( 1, i, 0) $ and $ ( 1, - i, 0) $; these are known as the circular points at infinity. The universe of the model comprises all points of the projective plane with the exception of the points of the straight line $ x _ {3} = 0 $, and all straight lines of the projective plane except $ x _ {3} = 0 $. In this case the automorphisms play the role of similarity transformations, but not merely motions as in non-Euclidean geometries.
The above models relate to two-dimensional geometries; the construction of projective models in a higher dimension is analogous.
References
| [1] | P.S. Aleksandrov, "What is non-Euclidean geometry?" , Moscow (1950) (In Russian) |
| [2] | F. Klein, "Nicht-Euklidische Geometrie: Vorlesungen gehalten während des Wintersemesters 1889–1890" , Göttingen (1893) |
| [3] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
Comments
For models of non-Euclidean geometries see also Beltrami interpretation; Klein interpretation; Poincaré model.
Instead of hyperbolic geometry one also finds the appellation Bolyai–Lobachevskii geometry, after the two codiscoverers.
References
| [a1] | R. Bonola, "Die nichteuklidische Geometrie" , Teubner (1908) (Translated from Italian) |
| [a2] | H.S. Carslaw, "The elements of non-Euclidean plane geometry and trigonometry" , Longman (1916) |
| [a3] | D.M.Y. Sommerville, "The elements of non-Euclidean geometry" , Dover, reprint (1958) |
| [a4] | H. Liebmann, "Nichteuklidische Geometrie" , Göschen (1912) pp. 114–119 |
| [a5] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 209 |
| [a6] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
| [a7] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a8] | H. Busemann, "Recent synthetic geometry" , Springer (1970) |
| [a9] | M. Greenberg, "Euclidean and non-Euclidean geometry" , Freeman (1980) |
| [a10] | P. Kelly, G. Matthews, "The non-Euclidean, hyperbolic plane" , Springer (1980) |
Non-Euclidean geometries. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-Euclidean_geometries&oldid=47982