Nine-point circle
2020 Mathematics Subject Classification: Primary: 51M15 [MSN][ZBL]
Euler circle, Feuerbach circle
A circle whose periphery contains the midpoints of the sides of a triangle, the bases of its altitudes, and the midpoints of the segment connecting the orthocentre of the triangle with the vertices. Its radius is equal to one-half of the radius of the circle circumscribed about the triangle. The nine-point circle of a triangle is tangent to the circle inscribed in it and to the three escribed circles. Let $H$ be the orthocentre of a non-equilateral triangle, let $T$ be the centre of gravity, let $O$ be the centre of the circumscribed circle and let $E$ be the centre of the nine-point circle. The points $H,T,O,E$ then lie on a straight line (the Euler line), $E$ being the midpoint of the segment $HO$, and the pair of points $H,T$ harmonically subdivides the pair of points $O,E$.
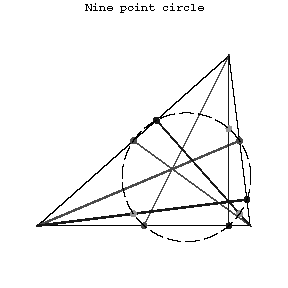
Figure: n066750a
References
| [1] | S.I. Zetel', "A new geometry of triangles" , Moscow (1962) (In Russian) |
| [2] | D.I. Perepelkin, "A course of elementary geometry" , 1 , Moscow-Leningrad (1948) (In Russian) |
Comments
Sometimes the nine-point circle is referred to as the Feuerbach circle. The fact that the nine-point circle is tangent to the inscribed circle and the three escribed circles is Feuerbach's theorem.
More generally one has the nine-point conic and the eleven-point conic determined by a projective base $\{a,b,c,d\}$ (giving a coordinate system) in the projective plane, cf. [a2], Sects. 16.5.5.1, 16.7.5.
References
| [a1] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
| [a2] | M. Berger, "Geometry" , 1–2 , Springer (1987) pp. Sects. 10.11.3, 17.5.4 (Translated from French) |
| [a3] | O. Veblen, J.W. Young, "Projective geometry" , II , Blaisdell (1946) pp. 169; 233 |
Nine-point circle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nine-point_circle&oldid=39655