Net
A two-parameter family of curves in a plane, or surfaces in space, that depends linearly on the parameters in the following way. Let $F_1,F_2,F_3$ be functions of two variables, no one of which is a linear combination of the other two. The family of curves in the plane that are defined by the equation
$$\lambda_1F_1+\lambda_2F_2+\lambda_3F_3=0$$
for all possible values of the parameters $\lambda_1,\lambda_2,\lambda_3$ (with the exception of $\lambda_1=\lambda_2=\lambda_3=0$) is a net (in fact, it depends on the ratios $\lambda_1:\lambda_2:\lambda_3$). The equation of a net of surfaces in space is written down in a similar way. The three equations $F_1=0$, $F_2=0$, $F_3=0$ give three elements of the net (three curves or surfaces) which determine the whole net.
A net of lines is a two-parameter family of straight lines lying on a surface. In Euclidean geometry a net of lines is the set of all straight lines that pass through a single point. If this point is a finite point, then the net is called elliptic, if it is a point at infinity, then the net is called parabolic.
A net of planes is a set of all planes that pass through a single point (a non-degenerate net) or that are parallel to some straight line (a degenerate net).
A net of circles is a two-parameter family of circles that depends linearly on the parameters. A non-degenerate net of circles is the set of all circles relative to which a given point (the centre of the net) has a given power. A degenerate net of circles is the set of all circles with centres on a certain fixed straight line (the so-called fundamental straight line) (see Fig. a).
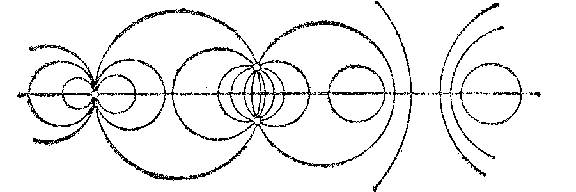
Figure: n066320a
If $(0,0)$ is the centre of a non-degenerate net, then its equation is
$$x^2+y^2-2ax-2by+p=0,\quad a^2+b^2>p,$$
where $a$ and $b$ are the parameters that define the circle and $p$ is the power of the centre of the net relative to its circles (the power of a degenerate net is assumed to infinite).
There are three types of non-degenerate nets of circles:
1) A hyperbolic circle net $(p>0)$, consisting of all circles that are orthogonal to a given circle (the fundamental circle) (see Fig. b).
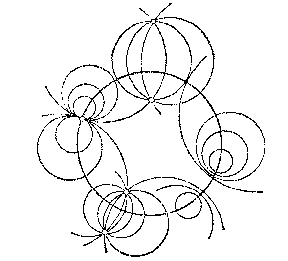
Figure: n066320b
2) A parabolic circle net $(p=0)$, consisting of all circles passing through a given point (the centre of the net) (see Fig. c).
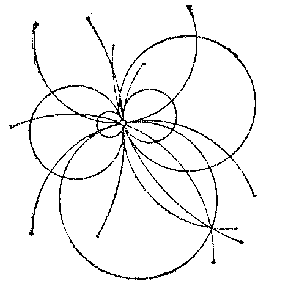
Figure: n066320c
3) An elliptic circle net $(p<0)$, consisting of circles that intersect a given circle in two diametrically-opposite points of the latter (see Fig. d).
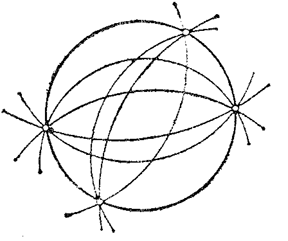
Figure: n066320d
The intersection of two nets of circles is a pencil of circles. An elliptic net contains only elliptic pencils, a parabolic net only elliptic and parabolic pencils, and a hyperbolic net contains three types of non-degenerate pencils. A degenerate net contains both degenerate and non-degenerate pencils of all three types.
The intersection of two nets one of which is elliptic can only be an elliptic pencil. The intersection of two nets one of which is parabolic can only be an elliptic or a parabolic pencil. The intersection of two nets one of which is non-degenerate can only be a non-degenerate pencil.
A net of spheres is a two-parameter family of spheres that depends linearly on the parameters. A net of spheres consists of the set of spheres relative to which the points of a certain line (the radical axis) have the same power (different for different points). The radical axis intersects all the spheres of the net in two points. Depending on whether these points are real (distinct), complex conjugates or coincident, a net of spheres is called elliptic (consisting of all the spheres through two common points), hyperbolic (consisting of all the spheres orthogonal to two intersecting spheres) or parabolic (consisting of all the spheres that touch a given line at a given point). The centres of all the spheres of a net lie on a plane perpendicular to the radical axis.
A net of spheres is the set of all spheres common to two webs of spheres (cf. Web of spheres).
In projective geometry, a net is the set of all lines, respectively, the set of all planes, that pass through a given point.
References
| [1] | M.M. Postnikov, "Analytic geometry" , Moscow (1973) (In Russian) |
| [2] | P.S. Modenov, "Analytic geometry" , Moscow (1969) (In Russian) |
Comments
Instead of the word "net" , for a $2$-dimensional linear system of curves or surfaces the word "bundlebundle" is also used.
References
| [a1] | J.A. Todd, "Projective and analytical geometry" , Pitman (1947) pp. Chapt. VI |
Net. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Net&oldid=32455