Negative curvature, surface of
(in the direct sense)
A two-dimensional surface in three-dimensional Euclidean space that has negative Gaussian curvature $ K < 0 $ at every point. The simplest examples of this are: a one-sheet hyperboloid (Fig.1a), a hyperbolic paraboloid (Fig.1b) and a catenoid.

Figure: n066200a
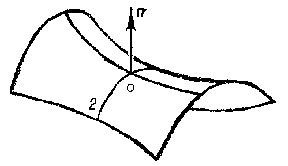
Figure: n066200b
The concept of a surface of negative curvature can be generalized, for example, with respect to the dimension of the surface itself or the dimension and structure of the ambient space.
Surfaces of negative curvature locally have a saddle-like structure. This means that in a sufficiently small neighbourhood of any of its points, a surface of negative curvature resembles a saddle (see Fig.1b, not considering the behaviour of the surface outside the part of it that has been drawn). The local saddle-like character of the surface is clearly illustrated in this figure, which shows the principal sections of the surface at an arbitrary point $ O $. Let $ 1/R _ {1} $, $ 1/R _ {2} $ be their normal curvatures, i.e. the principal curvatures at the point $ O $( cf. Principal curvature). According to the classical definition, the Gaussian curvature at $ O $ is the number $ K = 1/R _ {1} R _ {2} $. Since $ K < 0 $, the principal curvatures have different signs, for which reason the principal sections are convex in opposite directions; in Fig.1bthe section $ 0 2 $ is convex in the direction of the normal $ n $, while the other is convex in the opposite direction, which fits in with the saddle-like character of the surface. The topological structure in the large ( "globally" ) of a surface of negative curvature can be very different. For example, a hyperbolic paraboloid (Fig.1b) is topologically equivalent to the plane, while a one-sheet hyperboloid (Fig.1a) is equivalent to a cylindrical tube. Let two one-sheet hyperboloids with parallel axes intersect along a hyperbola (Fig.2a). Let these hyperboloids not be transparent, and let their invisible parts (i.e. the parts of any of them which lie within another) be disregarded. The surface thus obtained has negative curvature everywhere, apart from the points of the hyperbola mentioned above. At the points of this hyperbola there is, in general, no curvature (in the classical sense), since the hyperbola is an edge of the surface. However, the surface near the edge can, in the given case, be smoothed (see [7]), such that a surface is obtained that has a curvature at all points and that is, moreover, negative (see Fig.2b). It is topologically equivalent to a torus with two punctures. The topological structure of a surface of negative curvature can be made as complex as desired by the inclusion of a larger number of one-sheet hyperboloids.
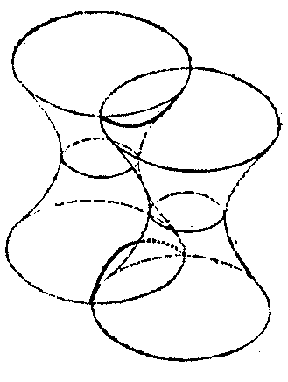
Figure: n066200c
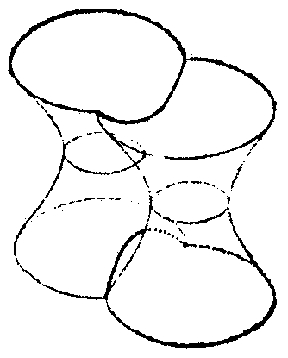
Figure: n066200d
A surface is said to be complete if it is a complete metric space with respect to the distance given by its intrinsic geometry (cf. also Internal metric). In all examples presented above, complete surfaces were considered. The idea of constructing complete surfaces of negative curvature of various topological types arising from very simple types (as shown above) is attributed to J. Hadamard [1]. A fundamentally different example is proposed in Fig. c(see [6], [7]). This surface has negative curvature everywhere, and is completely enclosed in a sphere. It has an infinite number of branches, and a variable point of it moving along the branches can get infinitely close to the boundary of the sphere without ever touching it. The surface is constructed such that a variable point moving along the branches always follows a path of infinite length. In this way, the completeness of the surface in the sense of its interior metric is guaranteed. This example shows that an intrinsically-complete surface of negative curvature does not necessarily move to infinity in space, like those in Hadamard's examples.
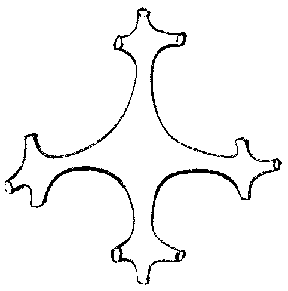
Figure: n066200e
In this example, the condition $ K < 0 $ can generally be observed, allowing for a slight irregularity of the surface. This means that the surface is presumed to be smooth (everywhere of class $ C ^ {1} $), but that at certain isolated points it does not belong to $ C ^ {2} $; at these points, the curvature must have a limit value. After completing the curvature with those limit values, it is defined everywhere and is continuous. The question of the extension of the surface and its connection with the condition of regularity is complemented by the following theorems [8].
If the Gaussian curvature $ K $ of a complete surface of class $ C ^ {2} $ satisfies the inequality $ - a ^ {2} \leq K \leq 0 $, where $ a = \textrm{ const } $, then the surface cannot be contained within a sphere of radius less than $ \sqrt 2/3 /a $.
If on a complete surface of class $ C ^ {2} $, which is unbounded in the intrinsic sense, the Gaussian curvature $ K \rightarrow 0 $ at infinity, then the surface is not bounded in space (in this theorem, the sign of the curvature may change).
Particular attention has been (and still is) paid to surfaces of constant negative curvature, i.e., they have Gaussian curvature with the same negative value at all points. They are notable for the fact that their intrinsic geometry locally coincides with the geometry on the Lobachevskii plane (see Lobachevskii geometry). This means that for figures which lie on a surface of constant negative curvature, precisely the same relations occur as those which hold in the Lobachevskii planimetry (the role of straight lines is played by geodesic lines); for example, the trigonometric formulas for triangles on a surface of constant negative curvature and the corresponding formulas in non-Euclidean Lobachevskii geometry coincide exactly. Thus, on a surface of constant negative curvature, a local model of the Lobachevskii geometry is obtained. A model of this type was constructed by E. Beltrami in 1868 (cf. Beltrami interpretation), which made an essential contribution to the recognition of Lobachevskii geometry. Beltrami also proposed an important example of a surface of negative curvature, which he called a pseudo-sphere (Fig. d) and which is formed by the rotation of a tractrix around its asymptote (Fig. e).
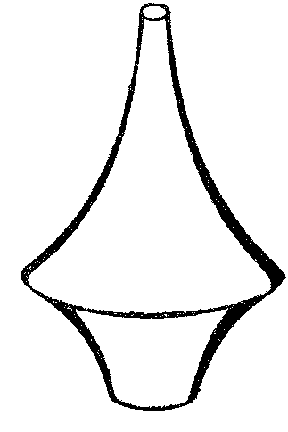
Figure: n066200f
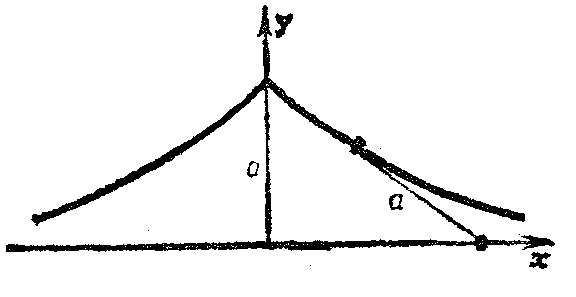
Figure: n066200g
A characteristic property of a tractrix is that the segment of the tangent from a point of tangency to the asymptote is constant and equal to a number $ a $. The Gaussian curvature of the pseudo-sphere is $ K = - 1/a ^ {2} $. Surfaces of rotation of negative curvature were studied even earlier than Beltrami by F. Minding in 1839. He discovered two forms of periodic surfaces of rotation of constant negative curvature (Fig. f) which, with the pseudo-sphere, exhaust all possible surfaces of rotation of constant negative curvature (for their equations, see [3], [5]).
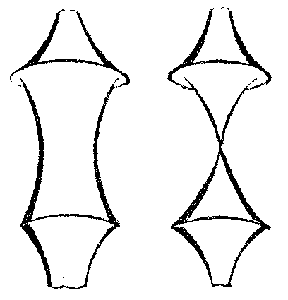
Figure: n066200h
The construction of a global model of Lobachevskii planimetry on a surface of rotation of constant negative curvature, for example on a pseudo-sphere, is not possible for two reasons. First, there are irregular points on a pseudo-sphere; these form a cuspidal edge (Fig. d). Secondly, a pseudo-sphere is topologically equivalent to a tube, and therefore, even from the topological point of view, differs from a Lobachevskii plane. However, it is possible to construct a model of the infinite part of the Lobachevskii plane on a regular surface of rotation of constant negative curvature. To this end, an infinite (contractible) domain $ U $ is cut out of the pseudo-sphere by a plane perpendicular to the axis. The plane is so formed that it does not contain the cuspidal edge. The part of the pseudo-sphere in which there is no cuspidal edge is taken as $ U $. Thereafter, only $ U $ is considered, and, for the sake of convenience, it is also called a pseudo-sphere; it has no singular points. Let $ U ^ \prime $ be the universal covering surface of $ U $. This concept can be introduced in the following way. A countably infinite number of identical and superposed copies of the pseudo-sphere $ U $ is taken, which are distinguished using the integers: $ \dots, U _ {-} 2 , U _ {-} 1 , U _ {0} , U _ {1} ,\dots $. Then they are all cut along a common meridian, and a left and right side of the cut is marked on each of them, such that all left sides are superposed (the same applies also to the right sides). Now, for any number $ k $, $ - \infty < k < \infty $, the left side of $ U _ {k} $ is joined to the right side of $ U _ {k+} 1 $( similarly, the right side of $ U _ {k} $ is joined to the left side of $ U _ {k-} 1 $). A connected surface $ U ^ \prime $ is thus obtained, which is also the universal covering surface of $ U $, and is sometimes called the simply-connected envelope of the surface $ U $. A universal covering can be constructed for any surface, but the visual description of its construction will be far less simple than that of a pseudo-sphere. It is essential that the universal covering is always simply connected. It is also important that the local intrinsic geometry of the covered surface can be transferred to the universal covering. For this to happen, it is sufficient to ensure that every point $ p $ of the covered surface has a convex neighbourhood $ V( p) $ which is covered one-sheetedly by a neighbourhood $ V ^ \prime ( p ^ \prime ) $ in the covering surface (here $ p ^ \prime $ is a point covering the point $ p $; the correspondence $ V \rightarrow V ^ \prime $ is bijective). The geometry of $ V( p) $ is transferred to $ V ^ \prime ( p ^ \prime ) $ identically, i.e. the distance between two points $ p _ {1} ^ \prime , p _ {2} ^ \prime \in V ^ \prime $ is taken to be equal to the distance between their inverse images. Then the global geometry of the universal covering is defined, but, as a rule, it will be completely different from the global geometry of the covered surface.
On the pseudo-sphere $ U $, the meridians, when moving towards infinity, converge; moreover, they are orthogonal to the boundary of $ U $. The boundary of the universal covering is therefore a curve in the Lobachevskii plane, which is the orthogonal trajectory of a pencil of Lobachevskii-parallel (converging) straight lines. This curve is called a horocycle in the Lobachevskii geometry. Thus, from the point of view of its intrinsic geometry, the universal covering of the pseudo-sphere $ U $ is the interior domain of an horocycle in the Lobachevskii plane. The universal covering $ U ^ \prime $ of the pseudo-sphere $ U $ is more convenient for the construction of a model of the Lobachevskii geometry than the pseudo-sphere $ U $ itself. E.g., a circle of any radius can be placed on $ U ^ \prime $, but a large circle without overlappings may prove to be too large to be contained in $ U $. However, even $ U ^ \prime $ is not extensive enough to contain some object of the Lobachevskii geometry, such as, for example, a complete straight line. In other words, it is not possible to construct a model of the entire Lobachevskii plane using $ U ^ \prime $.
In 1900, D. Hilbert posed the question of whether there exists a surface whose intrinsic geometry coincides completely with the geometry of the Lobachevskii plane. Using a simple reasoning, it follows that if such a surface does exist, it must have constant negative curvature and be complete. Moreover, it must be simply connected, since the Lobachevskii plane is simply connected. It would in fact be sufficient, however, to find a complete surface of constant negative curvature (as stated above, the universal covering of such a surface is complete and simply connected). In saying this, one considers only regular surfaces (at least twice continuously differentiable at any point, i.e. of class $ C ^ {2} $).
As early as 1901, Hilbert solved this problem (see [2]), and in the negative sense, so that no complete regular surface of constant negative curvature exists in three-dimensional Euclidean space. This theorem has attracted the attention of geometers over a number of decades, and continues to do so today. The reason for this is that a number of interesting questions are related to it and to its proof (see below). The occurrence of singular lines on surfaces of rotation of constant negative curvature (Fig. d, Fig. f) is not coincidental, but is in line with Hilbert's theorem.
The proof of Hilbert's theorem on surfaces of any topological structure is of special interest, since the concept of a universal covering surface is essential to it. This concept reduces the problem to a surface with the simplest topology, namely, a simply-connected surface. Hilbert's theorem was evidently one of the earliest mathematical statements to explain this concept. Following the publication of Hilbert's first article expounding the proof of his theorem, doubts were expressed on the validity of his proofs. The criticism related to the limitless behaviour of the asymptotic lines, which were studied on the surface in terms of the complexity of the topology of that surface. It was even suggested that Hilbert had refined his proof to make it more accurate. Nevertheless, Hilbert's proof was quite faultless throughout. These criticisms would probably not have arisen if Hilbert had stated clearly that the object of study was a complete simply-connected manifold of constant negative curvature, i.e. the Lobachevskii plane itself, assuming that it can be isometrically and regularly immersed in $ 3 $- dimensional Euclidean space.
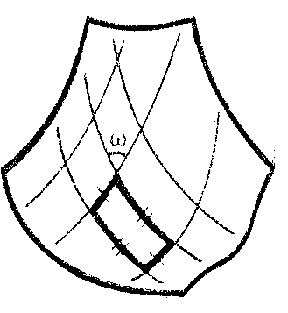
Figure: n066200i
It is also interesting that Chebyshev nets appear unexpectedly in Hilbert's proof. These are nets in which every net quadrangle has opposite sides of equal length (Fig. g). Moreover, an asymptotic net (which is defined and non-degenerate at all points on any surface of negative curvature) is a Chebyshev net in the case of a surface of constant negative curvature. This net can be taken to be a coordinate net: $ u = \textrm{ const } $, $ v = \textrm{ const } $. The line element then takes the Chebyshev form
$$ \tag{1 } ds ^ {2} = du ^ {2} + 2 \cos \omega du dv + dv ^ {2} , $$
where $ \omega $ is the angle in the net. Assuming that the surface is regular, complete and simply connected, and taking account of the Chebyshev nature of the net, it can be proved that $ u , v $ take all values: $ - \infty < u < \infty $, $ - \infty < v < \infty $; these exhaust all of the net. In other words, an asymptotic net in the large is homeomorphic to the Cartesian net on the Euclidean coordinate plane (see [9]). On the other hand, assuming that the Gaussian curvature is constant, for example $ K = - 1 $, the equation
$$ \tag{2 } \frac{\partial ^ {2} \omega }{\partial u \partial v } = \ \sin \omega $$
is obtained from (1), and the restrictions
$$ \tag{3 } 0 < \omega < \pi $$
follow from geometric considerations. Hilbert demonstrated that equation (2) cannot have a regular solution $ \omega = \omega ( u, v) $ subject to the condition (3) on the entire coordinate plane, and the complete Lobachevskii plane can therefore not be regularly and isometrically imbedded in $ 3 $- dimensional Euclidean space. As explained above, this leads to a more general formulation of this theorem: In $ 3 $- dimensional Euclidean space there does not exist a complete regular surface of constant negative curvature (whatever its topological structure).
In various areas of mathematics it happens that one particular statement or one particular question is of great importance in the development of the whole area. In differential geometry, Hilbert's theorem has been, and still remains, one such assertion, as witnessed by the amount of publications devoted to it. Interest in this theorem stems largely from the combination of different ideas and concepts in its proof (for example, the universal covering and the Chebyshev net). A connection with physics was subsequently established.
It turned out that equation (2), if written slightly differently and without restriction (3), proves to express a condition on the potential in the so-called Josephson effect from the theory of superconductivity. Physicists have named equation (2) the "sine-Gordon" equation. Using the connection between equation (2) and the theory of surfaces of negative curvature (see [13], [14]), certain solutions of the equation have been found in closed form, which are regular in the entire plane.
S.E. Cohn-Vossen proposed (see [15]) that a far more general theorem than Hilbert's theorem holds; namely, the condition on the Gaussian curvature $ K = \textrm{ const } < 0 $ can be replaced by the condition $ K \leq \textrm{ const } < 0 $. However, up to the beginning of the 1960's, no theorem had been found which included Hilbert's theorem as a specific case. Not until 1961 (see [16]) was the correctness of Hilbert's theorem proved, i.e. a theorem was proved concerning a surface of variable negative curvature, for which Hilbert's theorem is a limiting case. In other words, the properties of a surface of constant negative curvature, which give rise to the effect of Hilbert's theorem (disruption of regularity) and the effect itself, can be taken in an approximate sense. In the proof, an equation was found in the case of variable curvature, generalizing equation (2):
$$ \tag{4 } k ^ {2} \frac \partial {\partial s _ {2} } \left ( \frac{1}{K ^ {2} } \frac{\partial \omega }{\partial s _ {1} } \right ) = \ \{ k ^ {2} + A + \alpha | \mathop{\rm grad} \omega | \} \sin \ \omega , $$
where $ \omega $ has its previous sense, $ k ^ {2} = - K $, differentiation takes place along the arcs of the asymptotic lines, and $ A $ and $ \alpha $ are variables whose absolute values allow an intrinsic estimate, i.e. an estimate depending only on the imbedded metric. When $ K = \textrm{ const } $, then $ A = 0 $, $ \alpha = 0 $ are obtained, and equation (4) becomes equation (2).
In the case of variable curvature the equation
$$ \tag{5 } L _ {s _ {2} } L _ {s _ {1} } ^ {*} ( \omega ) = M \ \sin \omega $$
has been found (see [17]), where $ L _ {s _ {2} } $ is a linear operator proportional to the differentiation operator along the arc of the asymptotic lines of the second family, and $ L _ {s _ {1} } ^ {*} $ is a quasi-linear operator of similar structure. It is essential that the function $ M $, given certain conditions on the metric, has an intrinsic estimate from below by a positive number, thanks to which, and to the structure of the left-hand side, equation (5) is consistent with equation (2). Therefore, given these conditions on the metric, arguments can be put forward which are consistent with those of Hilbert (although far more complex) and which produce a similar result. In this way, a generalization of Hilbert's theorem was first obtained (see [18]). As regards the conditions on the metric mentioned above, they are included in the requirement that the Gaussian curvature $ K $ be bounded away from zero and changes slowly. It is proposed that if $ K \leq - 1 $, then a slow change of the curvature must be understood in the sense that the first and second derivatives of $ K $ along the arc of any geodesic are sufficiently small. Sufficient estimates are made such that in the calculation the above arguments, coming from Hilbert, can be used for equation (5). These estimates (see [19]) are expressed using positive constants, denoted by $ h $ and $ \Delta $. Consequently, metrics with a slowly-changing negative curvature are called $ ( h, \Delta ) $- metrics (for their definition see [18] or [19]); moreover, metrics of constant curvature are obtained when $ \Delta = + \infty $. Thus, a complete $ ( h, \Delta ) $- metric does not permit a regular isometric immersion in three-dimensional Euclidean space.
The question of generalizing Hilbert's theorem in the form in which it was stated in the 1930's (without restrictions on the character of the behaviour of the curvature, see [12]) along the lines indicated above, i.e. using differential equations of the theory of surfaces, has so far not succeeded at all. However, a solution to this problem has been obtained along entirely different lines, namely, through detailed studies of the boundary properties of the spherical image of a surface of negative curvature. Using this method, it has been proved ([19], [20]) that a complete metric with Gaussian curvature $ K \leq \textrm{ const } < 0 $ does not allow a regular isometric immersion in $ E ^ {3} $. This answers the question in the classical formulation. At the same time, the theorem that, in $ E ^ {3} $, the equality
$$ \tag{6 } \sup K = 0 $$
holds on every complete regular surface of negative Gaussian curvature $ K $, has been proved. Here, $ C ^ {2} $ regularity is sufficient. However (see [7]), in the case of $ C ^ {1,1} $ there is a counter-example (in the form of a weakly irregular surface). See [39] for these results.
Apart from (6), other equalities and estimates have been obtained (see [21]), which are universal in the sense that they refer to all surfaces of negative curvature in $ E ^ {3} $. Moreover, the method of proving (6) makes it possible to obtain theorems which give sufficient criterions for a mapping from a plane onto a plane with a negative Jacobian to be not only a local, but also a global diffeomorphism.
Despite the results which have now been obtained, studies on $ ( h, \Delta ) $- metrics and other metrics with slowly-changing curvature (for example, $ q $- metrics; see [9]) are still relevant. The situation is that for immersions of metrics with slowly-changing negative curvature, certain effects are created which do not occur in the case of more general metrics of negative curvature (see, for example, the theorem on the simple zone in [9]). As a rough rule, one can say that the slower the change of curvature, the "harder" it is for the metric of negative curvature to be immersed in $ E ^ {3} $. This is particularly noticeable in the case of a metric of constant curvature (see the strengthened Hilbert theorem [9]). As regards differential equations which arise in connection with the question of immersibility of $ ( h, \Delta ) $- metrics, they were essentially used in studies of other questions. Indeed, a number of strong theorems on the connection between intrinsic and extrinsic properties of surfaces of negative curvature has been proved using these equations; these include theorems on the dependence of the extrinsic regularity of the curvature of a surface of negative curvature on the regularity of its metric (see [7]).
The effect of the regularity of the metric on the extrinsic regularity of a surface with negative curvature is of particular interest, since surfaces of negative curvature form part of a special class of surfaces which can be defined purely geometrically (it is interesting that a purely geometric definition is also possible for the class of convex surfaces). Surfaces of this class are called saddle-like. Saddle-like surfaces are, in a certain sense, the antipodes of convex surfaces (see [22]–[25]).
The theorem on the non-existence in Euclidean space of a surface of complete negative curvature $ K \leq \textrm{ const } < 0 $ has a particularly strengthened form in the case of a surface which can be projected injectively onto a plane, i.e. which can be represented as the graph of a function $ z = f( x, y) $. In this case, universal estimates for the extension of the surface exist, and its completeness becomes immaterial. The following theorems have been proved (by N.V. Efimov, see [26]):
1) if a surface with Gaussian curvature $ K \leq - \alpha ^ {2} = \textrm{ const } < 0 $ can be regularly projected onto a rectangle with sides $ a, b $, then the inequality $ \sqrt \alpha \geq C _ {1} + \epsilon $, $ \epsilon > 0 $, implies $ a \sqrt \alpha \leq C _ {1} + C _ {2} / \epsilon $, where $ C _ {1} , C _ {2} $ are universal constants (for example, $ C _ {1} = 4 \pi $, $ C _ {2} = 12 \pi $);
2) if $ a, b $ are as above and (for the sake of simplicity) $ \alpha = 1 $, then $ a \leq 18.9 $.
Let a metric $ ds ^ {2} $ with negative Gaussian curvature $ K $ be given, and let $ k = \sqrt - K $. Let the metric $ ds ^ {2} $ be immersed in $ E ^ {3} $, and let $ l, m, n $ be the reduced coefficients of the second fundamental form (reduced means: satisfying the equation $ l n - m ^ {2} = - K $). In the immersion problem, $ l $, $ m $ and $ n $ are unknown functions. The Riemann invariants are introduced as new unknown functions:
$$ r = m+ \frac{k}{n} ,\ \ s = m- \frac{k}{n} . $$
The system of fundamental equations of the theory of surfaces will then take a symmetric form
$$ \tag{7 } \left . \begin{array}{c} r _ {x} + sr _ {y} = \ A _ {0} + A _ {1} r + A _ {2} s + A _ {3} r ^ {2} + A _ {4} rs + A _ {5} r ^ {2} s , \\ s _ {x} + rs _ {y} = \ A _ {0} + A _ {1} s + A _ {2} r + A _ {3} s ^ {2} + A _ {4} rs + A _ {5} s ^ {2} r, \end{array} \right \} $$
where $ A _ {0} \dots A _ {5} $ are expressed in terms of only the metric $ ds ^ {2} $.
It has already been shown that a complete surface of negative curvature with $ K \leq \textrm{ const } < 0 $ does not permit an isometric regular immersion in $ E ^ {3} $. The results obtained on the possibility of an isometric immersion of a two-dimensional manifold of negative curvature in $ E ^ {3} $ can be restricted to parts of complete manifolds. The manifold itself is taken to be simply connected. Thus, it has been proved (see [29], [30]) that every geodesic disc on an arbitrary regular manifold of negative curvature $ K \leq \textrm{ const } < 0 $ can be regularly isometrically immersed in $ E ^ {3} $. This theorem is obtained as a corollary of a more general theorem: Given certain natural conditions on the regularity of the metric of a complete surface of negative curvature with $ K \leq \textrm{ const } < 0 $, every infinite equidistant strip on this manifold can be isometrically and regularly immersed in $ E ^ {3} $. This theorem in turn is obtained as a result of the existence theorem of solutions of hyperbolic systems of quasi-linear equations of the form (7), where $ r \neq s $.
An example of a simply-connected manifold of sign-alternating curvature has been constructed on which there is a geodesic disc which cannot be isometrically immersed in $ E ^ {3} $( see [10]). It has been proved [31], given certain restrictions on the complete metric of a simply-connected surface of negative curvature $ K \leq \textrm{ const } < 0 $, that the interior of an arbitrary horocycle of such a manifold can be isometrically immersed in $ E ^ {3} $. Thus, for simply-connected manifolds of negative curvature $ K \leq \textrm{ const } < 0 $ it has been proved that isometric immersion is possible for all their compact and non-compact parts which are compatible with parts of the Lobachevskii plane, the isometric immersions of which are known through the works of Minding and Beltrami.
Immersions of a metric with Gaussian curvature $ K = \textrm{ const } < 0 $ have been studied, i.e. immersions of parts of the Lobachevskii plane. Thus, it has been proved that all polygons, even those of infinite extension, of the Lobachevskii plane can be isometrically immersed in $ E ^ {3} $; for new results on this kind of immersions see [40]–[42].
The variety of topological types of complete surfaces of negative curvature in $ E ^ {3} $ makes it necessary to consider different subclasses of this too large class, satisfying some supplementary conditions. The subclass of complete surfaces of negative curvature which have a one-to-one spherical ( "single-sheeted" ) mapping is particularly natural (see ). If a surface $ F $ of this class does not have self-intersections, then it is simply or doubly connected. If such a surface $ F $ has a horn, then, using the unboundedness of the saddle horn [34], a number of external geometric properties of this surface can be obtained: $ F $ can be defined by an equation $ z = f( x, y) $ over a domain obtained from the $ ( x, y) $- plane by eliminating a compact convex set; $ F $ has a bounding cone $ A( F ) $ consisting of a ray corresponding to the horn and a convex cone corresponding to the cup of the surface; the closure $ F ^ { * } $ of the spherical image of $ F $ has as its completion to a sphere an open semi-sphere and an open convex set (Fig. h–Fig. j).
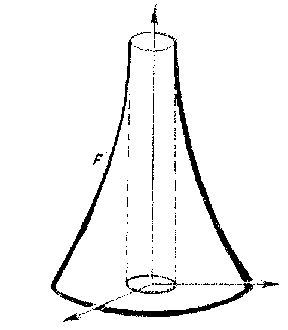
Figure: n066200j
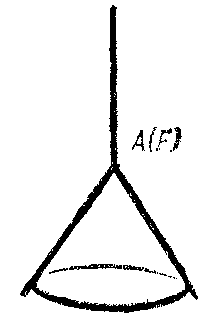
Figure: n066200k
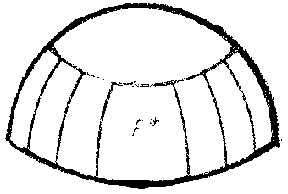
Figure: n066200l
A number of similar questions has been studied for other types of complete surfaces of negative curvature with a one-to-one spherical mapping.
Another class which is of interest because of its properties and the properties of its spherical mapping is the class of contractible surfaces of negative curvature (see , [37]). An example of this type of surface is the surface defined by an equation $ x ^ {2} y ^ {2} + y ^ {2} z ^ {2} + z ^ {2} x ^ {2} = a ^ {2} $. In a number of its properties, a contractible surface of negative curvature resembles a closed surface. Its spherical image can be viewed as a Riemann surface with boundary, each component of which is a spherical broken line lying on one of the large circles.
The theory of surfaces of negative curvature in a pseudo-Euclidean space $ E _ {2,1} ^ {3} $ is viewed differently. In this space, surfaces of negative curvature are convex; here the curvature is understood in the usual way, as the curvature of the metric induced by the ambient space. Namely, it is supposed to be negative.
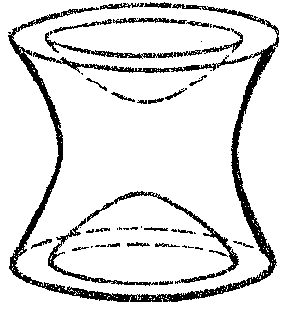
Figure: n066200m
The unit sphere of the space $ E _ {2,1} ^ {3} $ consists of three connected components, $ L _ {1} , L _ {2} , L _ {3} $( see Fig. k). The components $ L _ {1} $ and $ L _ {2} $ are convex surfaces on which a positive-definite metric of constant negative curvature is induced; these surfaces provide a well-known interpretation of the Lobachevskii geometry. The surface $ L _ {3} $ is saddle-like, and an indefinite metric of constant positive curvature is induced on it. The metric of this surface is known as the two-dimensional de Sitter metric.
Surfaces of negative curvature with a definite metric form a natural broad class of surfaces in $ E _ {2,1} ^ {3} $ generalizing the properties of the surfaces $ L _ {1} $ and $ L _ {2} $, just as surfaces of positive curvature form in Euclidean space a class generalizing the sphere (see [38]).
The properties of surfaces with a definite metric and negative curvature, the total curvature of which is finite, have been studied exhaustively. The properties of these surfaces are analogous to the properties of convex surfaces with curvature less than $ 2 \pi $ in Euclidean space (the class of Olovyanishnikov surfaces). Namely, a complete definite metric of negative curvature and finite total curvature $ \widetilde{K} $ and a geodesic ray $ \gamma $ on a manifold carrying this metric uniquely determine a convex surface with the given limiting cone of complete curvature $ \widetilde{K} $, without isotropic generators and with a given generator which is limiting for the ray $ \gamma $. The regularity of the surfaces obtained is determined by the regularity of the metric.
Complete surfaces of negative curvature with an indefinite metric are also convex. However, their properties are partially compatible with the properties of saddle-like surfaces in Euclidean space. In particular, the estimate $ \sup K = 0 $ holds for them. These surfaces would have to correspond to the component $ L _ {3} $ of the unit sphere of the space $ E _ {2,1} ^ {3} $, which is not convex, however. Here, both the sign of the Gaussian curvature and the sign of the determinant of the metric form of the surface play a determining role.
References
| [1] | J. Hadamard, "Les surfaces à courbures opposées et leurs lignes géodesique" J. Math. Pures Appl. , 4 (1898) pp. 27–73 |
| [2] | D. Hilbert, "Ueber Flächen von konstanter Gausscher Krümmung" , Gesammelte Abhandlungen , 2 , Springer (1933) pp. 437–448 |
| [3] | L. Bianchi, "Vorlesungen über Differentialgeometrie" , Teubner (1910) (Translated from Italian) Zbl 41.0676.01 |
| [4] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) MR0120537 Zbl 0211.23702 Zbl 0101.37601 Zbl 0052.37103 Zbl 0036.10002 Zbl 0061.31610 |
| [5] | A.P. Norden, "The theory of surfaces" , Moscow (1956) (In Russian) MR0082156 |
| [6] | E.R. Rozendorn, "The construction of a complete bounded surface with non-positive curvature" Uspekhi Mat. Nauk , 16 : 2 (1961) pp. 149–156 (In Russian) |
| [7] | E.R. Rozendorn, "Weakly irregular surfaces of negative curvature" Russian Math. Surveys , 21 : 5 (1966) pp. 57–112 Uspekhi Mat. Nauk , 21 : 5 (1966) pp. 59–116 MR0202093 Zbl 0173.23201 |
| [8] | Yu.A. Aminov, "The extrinsic diameter of a surface of negative curvature" Ukr. Geom. Sb. , 13 (1973) pp. 3–9 (In Russian) MR0334104 |
| [9] | N.V. Efimov, "Surfaces with slowly changing negative curvature" Russian Math. Surveys , 21 : 5 (1966) pp. 1–56 Uspekhi Mat. Nauk , 21 : 5 (1966) Zbl 0171.19903 |
| [10] | E.G. Poznyak, "Isometric immersions of two-dimensional Riemannian metrics in Euclidean space" Russian Math. Surveys , 28 : 4 (1973) pp. 47–77 Uspekhi Mat. Nauk , 28 : 4 (1973) pp. 47–76 Zbl 0289.53004 |
| [11] | E.G. Poznyak, E.V. Shikin, "Surfaces of negative curvature" J. Soviet Math. , 5 : 6 (1976) pp. 865–887 Itogi Nauk. i Tekhn. Ser. Algebra. Topol. Geom. , 12 (1974) pp. 171–207 Zbl 0107.15502 |
| [12] | E.G. Poznyak, "Geometric investigations connected with 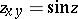 " J. Soviet Math. , 13 : 5 (1980) pp. 667–686 Itogi Nauk. i Tekhn. Probl. Geom. , 8 (1977) pp. 225–241 Zbl 0439.53006 " J. Soviet Math. , 13 : 5 (1980) pp. 667–686 Itogi Nauk. i Tekhn. Probl. Geom. , 8 (1977) pp. 225–241 Zbl 0439.53006 |
| [13] | I.V. Gribkov, "Construction of some regular solutions of the "sine-Gordon" equation by means of surfaces of constant negative curvature" Vestnik Mosk. Univ. Ser. Mat. Mekh. , 4 (1977) pp. 78–83 (In Russian) (English abstract) MR0467036 Zbl 0409.53017 Zbl 0359.53003 |
| [14] | I.V. Gribkov, "Some solutions of the sin-Gordon equation obtained by means of a Bäcklund transformation" Russian Math. Surveys , 33 : 2 (1978) pp. 231–232 Uspekhi Mat. Nauk , 33 : 2 (1978) pp. 191–192 |
| [15] | S.E. Cohn-Vossen, "Global deformation of surfaces" Uspekhi Mat. Nauk , 1 (1936) pp. 33–76 |
| [16] | N.V. Efimov, "The validity of Hilbert's theorem on surfaces of constant negative curvature" Soviet Math. Dokl. , 2 : 1 (1961) pp. 189–191 Dokl. Akad. Nauk SSSR , 136 : 6 (1961) pp. 1283–1286 MR137036 |
| [17] | N.V. Efimov, E.G. Poznyak, "Some transformations of the fundamental equations of the theory of surfaces" Soviet Math. Dokl. , 2 : 2 (1961) pp. 225–227 Dokl. Akad. Nauk SSSR , 137 : 1 (1961) pp. 25–27 MR130619 Zbl 0108.33901 |
| [18] | N.V. Efimov, E.G. Poznyak, "Generalization of Hilbert's theorem on surfaces of constant negative curvature" Soviet Math. Dokl. , 2 : 2 (1961) pp. 300–303 Dokl. Akad. Nauk SSSR , 137 : 3 (1961) pp. 509–512 MR130661 |
| [19] | N.V. Efmov, "Imposibility of a complete regular surface in euclidean 3-space whose Gaussian curvature has a negative upper bound" Soviet Math. Dokl. , 4 : 3 (1963) pp. 843–846 Dokl. Akad. Nauk SSSR , 150 : 6 (1963) pp. 1206–1209 |
| [20] | N.V. Efimov, "Generation of singularities on surfaces of negative curvature" Mat. Sb. , 64 : 2 (1964) pp. 286–320 (In Russian) |
| [21] | N.V. Efimov, "Differential criteria for homeomorphism of certain mappings with applications to the theory of surfaces" Math. USSR Sb. , 5 : 4 (1968) pp. 475–488 Mat. Sb. , 76 : 4 (1968) pp. 499–512 Zbl 0182.54702 |
| [22] | S.Z. Shefel', "Studies on the geometry of saddle-like surfaces" , Novosibirsk (1963) (In Russian) |
| [23] | S.Z. Shefel', "On the intrinsic geometry of saddle surfaces" Sib. Mat. Zh. , 5 : 6 (1964) pp. 1382–1396 (In Russian) |
| [24] | S.Z. Shefel', "A condition of compactness of a family of saddle surfaces" Siberian Math. J. , 8 : 3 (1967) pp. 528–535 Sib. Mat. Zh. , 8 : 3 (1967) pp. 705–714 Zbl 0161.41801 |
| [25] | S.Z. Shefel', "Saddle surfaces bounded by a rectifiable curve" Soviet Math. Dokl. , 6 : 3 (1965) pp. 684–687 Dokl. Akad. Nauk SSSR , 162 : 2 (1965) pp. 294–296 Zbl 0128.40601 |
| [26] | N.V. Efimov, "Estimates for the dimensions of the domains of regularity of solutions of certain Monge–Ampère equations" Math. USSR Sb. , 29 : 3 (1976) pp. 319–326 Mat. Sb. , 100 : 3 (1976) pp. 356–363 MR425786 Zbl 0376.35037 |
| [27] | N.V. Efimov, "Study of a single-valued projection of a surface of negative curvature" Dokl. Akad. Nauk SSSR , 93 : 4 (1953) pp. 609–611 (In Russian) |
| [28] | E. Heinz, "Ueber Flächen mit eindeutiger Projektion auf eine Ebene, deren Krümmungen durch Ungleichungen eingeschränkt sind" Math. Ann. , 129 : 5 (1955) pp. 451–454 Zbl 0065.37201 |
| [29] | E.G. Poznyak, "On the regular realization in the large of two-dimensional metrics of negative curvature" Soviet Math. Dokl. , 7 : 5 (1966) pp. 1288–1291 Dokl. Akad. Nauk SSSR , 170 : 4 (1966) pp. 786–789 Zbl 0168.19501 |
| [30] | E.G. Poznyak, "Regular global realization of two-dimensional metrics with negative curvature" Ukr. Geom. Sb. , 3 (1966) pp. 78–92 (In Russian) |
| [31] | E.V. Shikin, "On the global isometric imbedding in 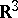 of some metrics of nonpositive curvature" Soviet Math. Dokl. , 15 : 2 (1974) pp. 448–451 Dokl. Akad. Nauk SSSR , 215 : 1 (1974) pp. 61–63 of some metrics of nonpositive curvature" Soviet Math. Dokl. , 15 : 2 (1974) pp. 448–451 Dokl. Akad. Nauk SSSR , 215 : 1 (1974) pp. 61–63 |
| [32] | B.L. Rozhdestvenskii, "A system of quasi-linear equations in the theory of surfaces" Dokl. Akad. Nauk SSSR , 143 : 1 (1962) pp. 50–52 (In Russian) |
| [33a] | A.L. Verner, "On the extrinsic geometry of elementary complete surfaces with nonpositive curvature I" Mat. USSR Sb. , 3 : 2 (1967) pp. 205–224 Mat. Sb. , 74 : 2 (1967) pp. 218–240 Zbl 0172.22702 |
| [33b] | A.L. Verner, "On the extrinsic geometry of elementary complete surfaces with nonpositive curvature II" Math. USSR Sb. , 4 : 1 (1968) pp. 99–123 Mat. Sb. , 75 : 1 (1967) pp. 112–139 Zbl 0176.18804 |
| [33c] | A.L. Verner, "Correction to "On the extrinsic geometry of elementary complete surfaces with nonpositive curvature" " Mat. Sb. , 77 : 1 (1968) pp. 136 (In Russian) MR0232323 |
| [34] | A.L. Verner, "Tapering saddle surfaces" Siberian Math. J. , 11 : 4 (1970) pp. 567–581 Sib. Mat. Zh. , 11 : 4 (1970) pp. 750–769 Zbl 0219.53052 |
| [35] | A.L. Verner, "The finiteness of the set of branch points of a spherical mapping of a narrowing saddle surface" Mat. Notes , 12 : 3 (1972) pp. 603–605 Mat. Zametki , 12 : 3 (1972) pp. 281–286 Zbl 0258.53009 |
| [36a] | D.D. Sokolov, "The structure of a limiting cone of a convex surface in Euclidean space" Uspekhi Mat. Nauk , 30 : 1 (1975) pp. 261–262 (In Russian) |
| [36b] | D.D. Sokolov, "On convex surfaces with an indefinite metric" Russian Math. Surveys , 33 : 4 (1978) pp. 265–266 Uspekhi Mat. Nauk , 33 : 4 (1978) pp. 227–228 Zbl 0414.53042 |
| [36c] | D.D. Sokolov, "Convex surfaces having bounded total curvature in pseudo-Euclidean space" Russian Math. Surveys , 34 : 3 (1979) pp. 222–223 Uspekhi Mat. Nauk , 34 : 3 (1979) pp. 213–214 Zbl 0437.53054 |
| [37] | A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian) |
| [38] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) MR0346714 MR0244909 Zbl 0311.53067 |
| [39] | T. Klotz Milnor, "Efimov's theorem about complete immersed surfaces of negative curvature" Adv. in Math. , 8 : 3 (1972) pp. 474–543 MR301679 |
| [40] | D.V. Tunitskii, "On the regular isometric immersion in  of unbounded domains of negative curvature" Mat. USSR Sb. , 62 : 1 (1989) pp. 121–138 Mat. Sb. , 134 : 1 (1987) pp. 119–134 MR912415 of unbounded domains of negative curvature" Mat. USSR Sb. , 62 : 1 (1989) pp. 121–138 Mat. Sb. , 134 : 1 (1987) pp. 119–134 MR912415 |
| [41] | Zh. Kaidasov, E.V. Shikin, "Isometric immersion in 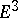 of a convex domain of the Lobachevskii plane containing two horocycles" Math. Notes , 39 : 4 (1986) pp. 335–340 Mat. Zametki , 39 : 4 (1986) pp. 612–617 of a convex domain of the Lobachevskii plane containing two horocycles" Math. Notes , 39 : 4 (1986) pp. 335–340 Mat. Zametki , 39 : 4 (1986) pp. 612–617 |
| [42] | Zh. Kaidasov, E.V. Shikin, "Isometric immersion in 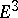 of extended strips on manifolds of type of extended strips on manifolds of type 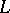 " Math. Notes , 42 : 6 (1987) pp. 962–968 Mat. Zametki , 42 : 6 (1987) pp. 842–851 " Math. Notes , 42 : 6 (1987) pp. 962–968 Mat. Zametki , 42 : 6 (1987) pp. 842–851 |
Comments
The Hilbert result that a surface of constant negative curvature cannot be imbedded isometrically in $ E ^ {3} $ needs $ C ^ {2} $ regularity. The general method of $ C ^ {1} $ isometric imbedding, [a1], [a2], applies also here.
References
| [a1] | N.H. Kuiper, "On 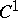 -isometric imbeddings I" Indag. Math. , 17 : 4 (1955) pp. 545–556 MR75640 -isometric imbeddings I" Indag. Math. , 17 : 4 (1955) pp. 545–556 MR75640 |
| [a2] | N.H. Kuiper, "On 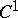 -isometric imbeddings II" Indag. Math. , 17 : 5 (1955) pp. 683–689 MR75640 -isometric imbeddings II" Indag. Math. , 17 : 5 (1955) pp. 683–689 MR75640 |
| [a3] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) MR0917479 Zbl 0629.53001 |
| [a4] | W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German) MR0474045 Zbl 0366.53001 |
| [a5] | D.J. Struik, "Lectures on classical differential geometry" , Addison-Wesley (1961) MR0939369 MR1528072 MR0036551 Zbl 0105.14707 |
| [a6] | A.V. Pogorelov, "Intrinsic geometry of surfaces" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [a7] | M. Spivak, "A comprehensive introduction to differential geometry" , 3; 5 , Publish or Perish (1975) pp. 1–5 MR0394453 MR0394452 MR0372756 Zbl 0306.53003 Zbl 0306.53002 Zbl 0306.53001 |
| [a8] | M. Gromov, "Partial differential relations" , Springer (1986) (Translated from Russian) MR0864505 Zbl 0651.53001 |
| [a9] | M. Gromov, "Embeddings and immersions in Riemannian geometry" Russian Math. Surveys , 25 : 5 (1970) pp. 1–58 Uspekhi Mat. Nauk , 25 : 5 (1970) pp. 3–62 Zbl 0222.53053 Zbl 0202.21004 |
Negative curvature, surface of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Negative_curvature,_surface_of&oldid=47952