Modular function
elliptic modular function, of one complex variable
An automorphic function of a complex variable  , associated with the group
, associated with the group 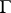 of all fractional-linear transformations
of all fractional-linear transformations 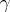 of the form
of the form
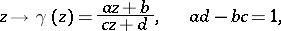 | (1) |
where  are real integers (this group is called the modular group). The transformations of
are real integers (this group is called the modular group). The transformations of 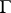 transform the real axis into itself and the domain of definition of a modular function can be regarded as being the upper half-plane
transform the real axis into itself and the domain of definition of a modular function can be regarded as being the upper half-plane 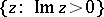 . The group
. The group 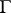 is generated by the two transformations
is generated by the two transformations 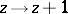 ,
, 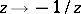 .
.
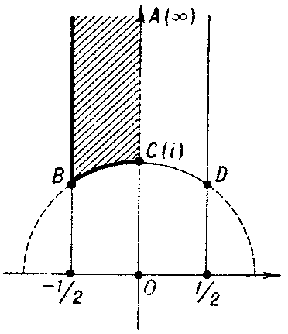
Figure: m064430a
A fundamental domain  of the modular group is depicted in Fig. a; this is the curvilinear quadrangle
of the modular group is depicted in Fig. a; this is the curvilinear quadrangle  with vertices
with vertices  ,
, 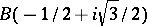 ,
, 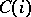 ,
, 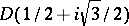 two sides of which,
two sides of which, 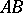 and
and  , are segments of the lines
, are segments of the lines 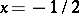 and
and  , respectively, and
, respectively, and 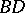 is an arc of the circle
is an arc of the circle  .
. 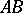 and
and 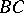 are included in
are included in 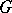 ,
, 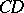 and
and 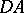 are not. The images of
are not. The images of 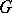 under all possible mappings of
under all possible mappings of 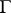 cover the half-plane
cover the half-plane  without intersections.
without intersections.
The study of modular functions began in the 19th century in connection with the study of elliptic functions and preceded the appearance of the general theory of automorphic functions. In the theory of modular functions the following theta-series are used as basic modular forms:
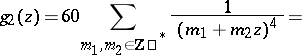 |
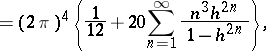 |
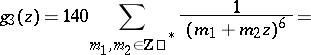 |
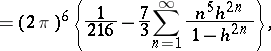 |
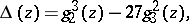 |
where 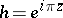 and the asterisk means that the null pair
and the asterisk means that the null pair  is omitted. According to the terminology of K. Weierstrass these are relative invariants, playing a major role in his theory of elliptic functions (see Weierstrass elliptic functions), and
is omitted. According to the terminology of K. Weierstrass these are relative invariants, playing a major role in his theory of elliptic functions (see Weierstrass elliptic functions), and 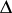 is also called the discriminant. From the point of view of the theory of automorphic functions (cf. Automorphic function; Automorphic form) these are automorphic forms of weights
is also called the discriminant. From the point of view of the theory of automorphic functions (cf. Automorphic function; Automorphic form) these are automorphic forms of weights  ,
,  and
and 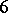 , respectively, associated with the modular group. The fundamental modular form has the form
, respectively, associated with the modular group. The fundamental modular form has the form
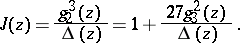 | (2) |
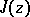 is also called the absolute invariant. It is regular in the upper half-plane and in the interior of the fundamental domain
is also called the absolute invariant. It is regular in the upper half-plane and in the interior of the fundamental domain  it takes each finite value, except
it takes each finite value, except  and
and 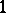 , precisely once; in addition,
, precisely once; in addition, 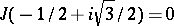 ,
, 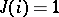 .
.
The modular function 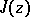 plays a major role in the theory of elliptic functions, allowing one to determine the periods
plays a major role in the theory of elliptic functions, allowing one to determine the periods 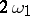 ,
,  with respect to given Weierstrass relative invariants
with respect to given Weierstrass relative invariants 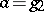 ,
, 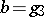 ,
, 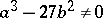 , and, consequently, to construct all Weierstrass elliptic functions. If
, and, consequently, to construct all Weierstrass elliptic functions. If  is the unique solution in the fundamental domain of the equation
is the unique solution in the fundamental domain of the equation
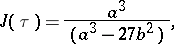 |
then for 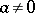 ,
, 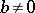 one has
one has 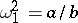 ,
,  ; for
; for 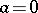 one has
one has 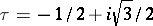 , and
, and 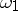 is determined by the equation
is determined by the equation
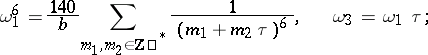 |
for 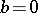 one has
one has 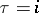 , and
, and 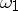 is determined by the equation
is determined by the equation
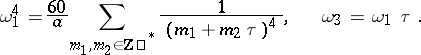 |
For the construction of Jacobi elliptic functions, instead of  it is more convenient to use
it is more convenient to use
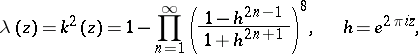 | (3) |
also called a modular function. By the same token, 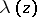 is an automorphic function only relative to the subgroup
is an automorphic function only relative to the subgroup 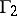 of
of 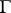 , where
, where 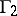 consists of all transformations of the form (1) in which (as an extra condition)
consists of all transformations of the form (1) in which (as an extra condition)  and
and 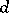 are odd numbers and
are odd numbers and 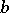 and
and  are even. The fundamental domain
are even. The fundamental domain  of
of 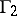 is depicted in Fig. b; this is the curvilinear quadrangle
is depicted in Fig. b; this is the curvilinear quadrangle 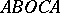 with vertices
with vertices 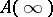 ,
, 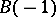 ,
,  ,
, 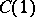 , two sides of which,
, two sides of which, 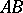 and
and 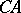 , are segments of the lines
, are segments of the lines 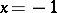 and
and  , respectively, and
, respectively, and 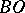 and
and 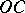 are arcs of the circles
are arcs of the circles 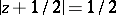 and
and 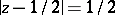 , respectively. The parts of the boundary to the left of the imaginary axis are included and
, respectively. The parts of the boundary to the left of the imaginary axis are included and 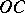 and
and 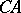 are not included.
are not included.

Figure: m064430b
The function 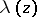 is also regular in the upper half-plane
is also regular in the upper half-plane 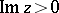 . In the interior of
. In the interior of 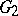 it takes each finite value, except
it takes each finite value, except  and
and 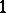 , precisely once; in addition,
, precisely once; in addition, 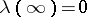 and
and 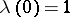 . For the construction of a Jacobi elliptic function of given modulus
. For the construction of a Jacobi elliptic function of given modulus  the value
the value 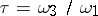 , or
, or 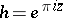 , uniquely defined by the equation
, uniquely defined by the equation 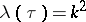 , is required. In practice, in the normal case
, is required. In practice, in the normal case 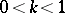 , one first determines
, one first determines 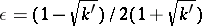 , where
, where 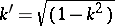 , and then constructs a solution of this equation in the form of a series
, and then constructs a solution of this equation in the form of a series 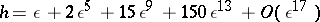 . The modular functions
. The modular functions  and
and  are related by
are related by
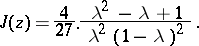 |
The modular function 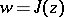 gives the most convenient representation of the conformal classes of Riemann surfaces of elliptic functions (cf. Riemann surfaces, conformal classes of), when the genus
gives the most convenient representation of the conformal classes of Riemann surfaces of elliptic functions (cf. Riemann surfaces, conformal classes of), when the genus  and the Euler characteristic
and the Euler characteristic 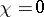 . Corresponding to each
. Corresponding to each 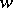 there is a solution
there is a solution 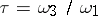 of
of 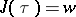 , which determines a conformal class and the corresponding field of elliptic functions. For example,
, which determines a conformal class and the corresponding field of elliptic functions. For example, 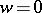 corresponds to a period parallelogram in the form of a rhombus with angles
corresponds to a period parallelogram in the form of a rhombus with angles 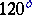 and
and 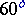 , and
, and 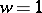 corresponds to a square. Modular functions have also been applied in the study of conformal mapping; boundary properties of analytic functions and cluster sets (cf. Cluster set). The modular function
corresponds to a square. Modular functions have also been applied in the study of conformal mapping; boundary properties of analytic functions and cluster sets (cf. Cluster set). The modular function 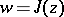 gives a conformal mapping of the left half of the fundamental domain
gives a conformal mapping of the left half of the fundamental domain 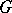 (Fig. a), that is, the curvilinear triangle
(Fig. a), that is, the curvilinear triangle 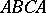 , onto the upper half-plane
, onto the upper half-plane  , where
, where 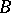 ,
, 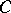 and
and 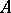 are mapped to
are mapped to  ,
,  and
and 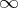 , respectively. The modular function
, respectively. The modular function 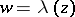 conformally maps the curvilinear triangle
conformally maps the curvilinear triangle 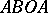 (Fig. b) onto the upper half-plane, where
(Fig. b) onto the upper half-plane, where 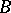 ,
, 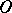 and
and 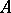 are mapped to
are mapped to  ,
, 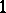 and
and 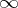 , respectively.
, respectively.
In geometric questions it is often more convenient to take the unit disc as the domain of the modular functions. The modular group (1) is then replaced by the modular group of automorphisms of the unit disc. For example, it is convenient to apply the fractional-linear transformation
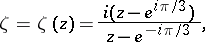 |
which maps the upper half-plane 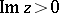 onto the unit disc
onto the unit disc 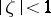 , where
, where  ,
, 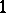 and
and 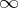 are mapped to
are mapped to 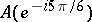 ,
, 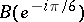 and
and  , respectively, on the unit circle
, respectively, on the unit circle 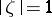 (Fig. c).
(Fig. c).

Figure: m064430c
Then the composite function 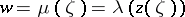 is a modular function that is regular in the unit disc and takes there all values except
is a modular function that is regular in the unit disc and takes there all values except  ,
, 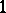 and
and 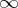 . It conformally maps the curvilinear triangle
. It conformally maps the curvilinear triangle 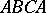 (Fig. c) onto the upper half-plane
(Fig. c) onto the upper half-plane 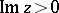 . It is precisely this modular function
. It is precisely this modular function 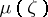 that is used in the proof of the Picard theorem and in a number of geometric questions.
that is used in the proof of the Picard theorem and in a number of geometric questions.
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1964) pp. Chapt.8 |
| [2] | N.I. Akhiezer, "Elements of the theory of elliptic functions" , Amer. Math. Soc. (1990) (Translated from Russian) |
| [3] | L.R. Ford, "Automorphic functions" , Chelsea, reprint (1951) |
| [4] | F. Klein, R. Fricke, "Vorlesungen über die Theorie der elliptischen Modulfunktionen" , 1–2 , Teubner (1890–1892) |
Comments
When considering the upper half-plane and the modular group acting on it, the point  and the rational points on the real axis are often referred to as cusps.
and the rational points on the real axis are often referred to as cusps.
More generally, consider the group 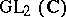 of invertible complex
of invertible complex 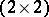 -matrices,
-matrices, 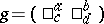 , and the corresponding fractional-linear transformations
, and the corresponding fractional-linear transformations
 | (a1) |
The fractional-linear transformation (a1) is called parabolic if it is  and the associated matrix has two equal eigen values (cf. also Fractional-linear mapping). This is equivalent to saying that the Jordan canonical form is of the form
and the associated matrix has two equal eigen values (cf. also Fractional-linear mapping). This is equivalent to saying that the Jordan canonical form is of the form 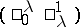 , or, if
, or, if 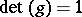 is also imposed, that
is also imposed, that  . Now let
. Now let  be some discrete subgroup of
be some discrete subgroup of 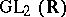 . A point
. A point 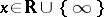 is called a cusp of
is called a cusp of 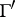 if there is a parabolic element of
if there is a parabolic element of 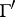 which has
which has  as a fixed point.
as a fixed point.
The cusps of 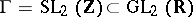 are precisely the points of
are precisely the points of 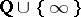 . To aid visualization, cf. Fig. a, the point
. To aid visualization, cf. Fig. a, the point 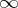 is written as
is written as 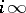 (
( the point
the point 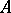 in Fig. a).
in Fig. a).
Let 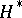 be the extended upper half-plane
be the extended upper half-plane  , where
, where  . The action of
. The action of 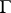 on
on 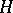 naturally extends to
naturally extends to 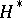 , and all the points of
, and all the points of 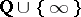 form one orbit. The translates of the fundamental region
form one orbit. The translates of the fundamental region 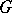 of Fig. aform a tesselation of
of Fig. aform a tesselation of 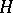 (or of
(or of 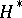 ), called the modular tesselation. Each translate
), called the modular tesselation. Each translate 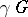 ,
, 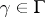 , is called a modular triangle. In the special points
, is called a modular triangle. In the special points 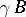 ,
, 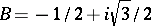 ,
, 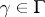 , six modular triangles meet; in the special points
, six modular triangles meet; in the special points 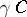 ,
, 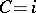 ,
, 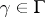 , two modular triangles meet; and in a cusp (a point of
, two modular triangles meet; and in a cusp (a point of 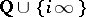 ) countably infinite many modular triangles meet (at angle 0; whence the terminology "cusp" ).
) countably infinite many modular triangles meet (at angle 0; whence the terminology "cusp" ).
The modular functions form a field. Indeed, this is the field 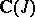 , where
, where 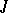 is the fundamental modular function (2) above.
is the fundamental modular function (2) above.
Let 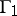 be a subgroup of finite index in
be a subgroup of finite index in 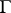 . The quotient
. The quotient 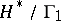 can be given a natural complex structure making it a compact Riemann surface, cf. e.g. [a1], Chapt. IV, § 6. This is a natural compactification of
can be given a natural complex structure making it a compact Riemann surface, cf. e.g. [a1], Chapt. IV, § 6. This is a natural compactification of  . For
. For  one finds the Riemann sphere (of genus zero). For the principal congruence subgroups
one finds the Riemann sphere (of genus zero). For the principal congruence subgroups
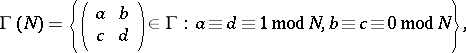 |
the resulting quotients  , the modular curves
, the modular curves  , for
, for 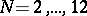 have genus 0, 0, 0, 0, 1, 3, 5, 10, 13, 26, 25, respectively. For the general formula cf. Modular curve.
have genus 0, 0, 0, 0, 1, 3, 5, 10, 13, 26, 25, respectively. For the general formula cf. Modular curve.
A modular function for a subgroup of finite index 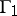 of
of 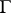 is a complex meromorphic function
is a complex meromorphic function 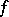 on
on 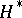 such that
such that  for
for 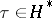 ,
, 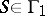 , and such that at a rational cusp
, and such that at a rational cusp 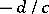 ,
, 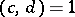 ,
, 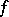 admits an expansion of the form
admits an expansion of the form
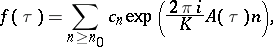 |
for some 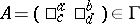 , natural number
, natural number 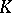 and
and 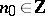 . This is valid for
. This is valid for  with
with 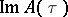 large enough. This last condition reflects the requirement that
large enough. This last condition reflects the requirement that 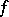 also defines a meromorphic function on the compactification
also defines a meromorphic function on the compactification  of
of 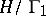 , cf. Automorphic function. In case
, cf. Automorphic function. In case  this last requirement takes the following form: There is an
this last requirement takes the following form: There is an 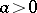 such that for
such that for 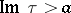 ,
, 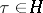 ,
, 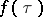 has an expansion of the form
has an expansion of the form
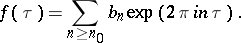 |
References
| [a1] | B. Schoeneberg, "Elliptic modular functions" , Springer (1974) |
| [a2] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Princeton Univ. Press (1971) |
| [a3] | R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977) |
| [a4] | S. Lang, "Elliptic functions" , Addison-Wesley (1973) |
Modular function. E.D. Solomentsev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modular_function&oldid=14166