Linear operator

linear transformation, linear map

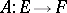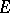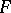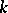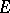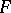A mapping between two vector spaces (cf. Vector space) that is compatible with their linear structures. More precisely, a mapping , where and are vector spaces over a field , is called a linear operator from to if

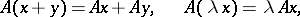for all 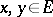, 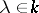. The simplest examples are the zero linear operator 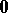, which takes all vectors into 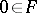, and (in the case 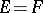) the identity linear operator 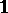, which leaves all vectors unchanged.

The concept of a linear operator, which together with the concept of a vector space is fundamental in linear algebra, plays a role in very diverse branches of mathematics and physics, above all in analysis and its applications.

The modern definition of a linear operator was first given by G. Peano [1] (for 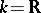). However, it was rooted in the previous developments of mathematics, which had accumulated (beginning with the linear function 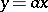) a vast number of examples. In algebra an incomplete list of them includes linear substitutions in systems of linear equations, and multiplication of quaternions and elements of a Grassmann algebra; in analytic geometry it includes coordinate transformations; in analysis it includes differential and integral transforms and the Fourier integral.

Up to the beginning of the 20th century the only linear operators that had been systematically studied were those between finite-dimensional spaces over the fields 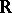and 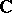. The first "infinite-dimensional" observations, concerned also with general fields, were made by O. Toeplitz [3]. As a rule, linear operators between infinite-dimensional spaces 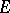and 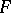are studied under the assumption that they are continuous with respect to certain topologies. Continuous linear operators that act in various classes of topological vector spaces, in the first place Banach and Hilbert spaces, are the main object of study of linear functional analysis (cf. also Banach space; Hilbert space; Topological vector space).

In the theory of linear operators the two special cases 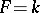and are the most important. In the first case a linear operator is called a functional (see Linear functional), and in the second case a linear transformation of $E$ (see Linear transformation), a linear operator acting in 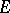, or an endomorphism.

The linear operators from to 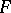form a vector space 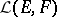(for 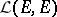one writes 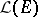) over 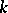with respect to addition and multiplication by a scalar, given by the formulas

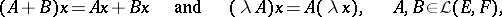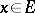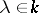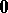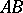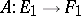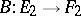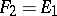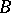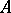, ; the zero is . Multiplication (composition) of linear operators and is defined only for as the successive application of and . With respect to these three operations 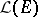is an example of an associative algebra over 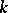with identity 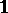(cf. Associative rings and algebras). This is "more than an example" : Every associative algebra over 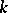can be imbedded in an 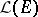for some .

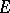Vector spaces over a fixed field (objects) and linear operators (morphisms) form, together with the composition law, the category 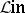. The following concepts are special cases (in connection with ) of general categorical concepts. For a linear operator 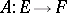its kernel (or null-space) is the subspace , its image is the subspace 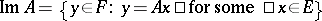, and its cokernel is the quotient space . The rank of a linear operator is the dimension of its kernel and the nullity is the dimension of its kernel. A linear operator 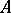is called a monomorphism if and an epimorphism if 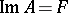. A linear operator 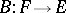is called a left (respectively, right) inverse o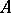f if 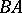is the identity in 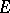(respectively, 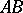is the identity in 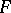). A linear operator 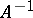that is simultaneously the left and right inverse of 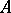is called the inverse of 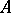. A linear operator (respectively, endomorphism) that has an inverse is called an isomorphism (respectively, automorphism).

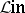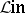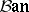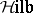The category is an Abelian category with respect to addition of linear operators; in particular, a linear operator that is a monomorphism and an epimorphism is an isomorphism. Moreover, in every monomorphism has a left inverse and every epimorphism has a right inverse. By analogy with one introduces the categories and ; the objects of the first are Banach spaces, and the objects of the second are Hilbert spaces; the morphisms in both are continuous linear operators. Both categories are additive (cf. Additive category), but not Abelian. Isomorphisms in them are called topological isomorphisms; these are linear operators that have a continuous inverse.

One of the most important typical problems of the "intrinsic" theory of linear operators is the problem of classifying endomorphisms (or at least certain classes of them) with respect to some equivalence or other. For linear operators in pure algebra one considers, as a rule, the general categorical equivalence of endomorphisms in 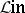; it is called similarity. In other words, linear operators 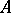and 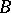acting in 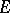and 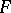, respectively, are similar if for some isomorphism 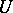the diagram

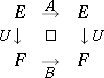(1)

commutes. Equivalence of continuous linear operators in (general) Banach spaces is called topological equivalence, and is understood in the general categorical sense, this time in 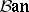; this implies that the diagram (1) commutes for some topological isomorphism 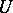. For linear operators in Hilbert spaces one chooses unitary equivalence of 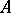and 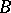as basis, corresponding to the requirement that the diagram (1) commutes for some unitary (see below) operator .

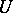Besides this, in the theory of linear operators between spaces with a topology there are important problems of approximating various classes of linear operators by operators of a comparatively simple structure. A significant role is played by problems about finding the general form of linear operators on concrete spaces, most frequently function spaces.

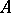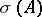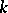Among the invariants of similarity the most important are the spectrum and the number of invariant subspaces of given dimension. Let be a linear operator on . Its spectrum is the subset in consisting of those 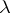for which 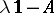has no inverse. A subspace 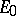of 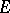is said to be invariant with respect to 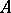if 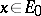implies that 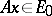. Besides the kernel and the image of a linear operator, examples are the one-dimensional subspaces containing the so-called eigen vectors of the operator, that is, those 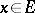, , 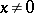for which 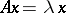, 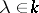. The element 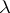, called an eigen value of 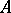, automatically belongs to 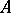's spectrum.

The concept of a linear operator is a special case of the concept of a morphism of modules, which is obtained by replacing the field by an arbitrary ring. In many respects morphisms of modules are not like linear operators in their properties, but results about the latter form one of the stimuli for studying them.

Linear operators on finite-dimensional spaces

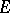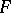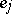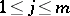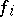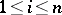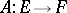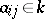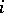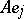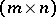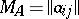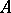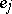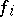(without additional structure). The main analytic apparatus for such linear operators is the matrix notation. Let and be spaces with fixed bases , , and , , let be a linear operator, and let be the -th coefficients of the expansion of with respect to the second basis. Then the -dimensional matrix is called the matrix of the linear operator in the bases and . If 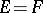the matrix notation is usually taken in coincident bases (that is, 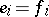, 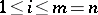). By transfer to other bases the matrix of a linear operator is changed by simple formulas.

To various characteristics of linear operators correspond, as a rule, effectively computable characteristics of their matrices. For example, 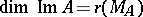and 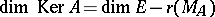, where is the rank of the matrix; in particular, 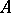is an isomorphism if and only if 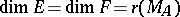; this condition is equivalent to the determinant of 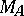being non-zero. To algebraic operations on linear operators correspond operations of the same name on their matrices, taken in fixed bases.

Linear operators are similar if and only if they can be described (each in its "own" basis) by the same matrix. The eigen values of a linear operator are the roots of the characteristic polynomial of its matrix. This implies that every linear operator on a finite-dimensional space over an algebraically closed field (for example, 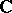) has at least one eigen vector. The spectrum of a linear operator on a finite-dimensional space over an arbitrary field is the set of its eigen values.

The problem of classifying endomorphisms of finite-dimensional spaces over an algebraically closed field has been completely solved, and the similarity classes have been described in terms of the invariant subspaces. The main step here is the following classification theorem, discovered by C. Jordan (who considered the field 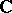). A matrix with a fixed 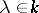on the main diagonal, ones immediately above it and zeros elsewhere, is called a Jordan block, and a block matrix with Jordan blocks (of different dimensions and with different 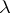) on the main diagonal and zeros elsewhere is called a Jordan matrix. Then every endomorphism can be written in some basis as a Jordan matrix. The search for such a basis is called reduction of a linear operator to Jordan form. Since linear operators described by Jordan matrices are similar if and only if their matrices coincide up to a permutation of the Jordan blocks, the theorem means that Jordan matrices present, after suitable identification, a complete set of similarity invariants.

Continuous linear operators on Banach spaces.

The foundations of this theory were laid by S. Banach (see [4]).

Examples.

1) In 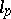(from now on, 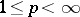): the linear operator of multiplication by a bounded sequence of numbers; the linear operator of left (respectively, right) shift, which takes 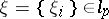to (respectively, to ).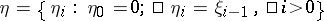

2) In 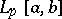or 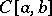: the linear operator of multiplication by a continuous functi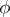on on 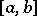; the linear operator of indefinite integration, which takes 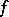to ,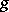

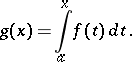3) In 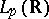: the linear operator of a shift by 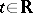, which takes 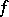to , .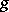

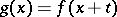4) From 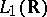into 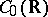: The "classical" Fourier operator, which takes 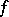to ,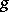

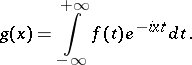A linear operator 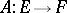between Banach spaces is continuous if and only if it is bounded, that is, the image of every bounded set in 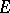is bounded in 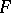, or equivalently, if there is a (finite) number 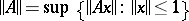, called the operator norm (a similar assertion is also true for arbitrary normed spaces). The continuous linear operators from 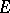into 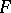form a subspace 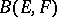of 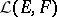which is a Banach space with respect to 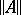. The subspace 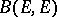, often denoted by 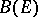, is even a Banach algebra with respect to operator multiplication. The class of these algebras is universal in the sense that every Banach algebra is topologically isomorphic to a subalgebra of 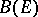for some 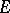. The subset of 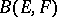consisting of topological isomorphisms is open and for 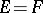contains the open ball of unit radius with centre at .

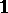A fundamental role in the "Banach" theory of linear operators is played by two theorems, which together with the Hahn–Banach theorem (see also Linear functional) are called the three fundamental principles of linear analysis. The simplest form of the "principle of uniform boundedness" is the Banach–Steinhaus theorem: If continuous linear operators , 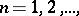are such that for every 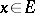one has 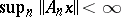, then . The simplest form of the "open mapping principle" is Banach's theorem: If a continuous linear operator has an inverse, then this inverse operator is automatically continuous. The requirement that the spaces be "Banach" (complete) spaces is essential in both theorems.

The spectrum of a continuous linear operator 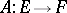, usually considered for complex spaces, is a non-empty compact set in 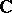. In the case of an infinite-dimensional space the set of eigen values of a linear operator, called the point spectrum, generally forms only part of 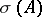. For the remaining 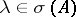one always has 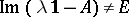; these numbers split into two sets, the continuous spectrum and the residual spectrum, according as 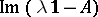is dense in 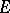or not. For example, the spectrum of the linear operator of multiplication by 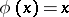is the interval 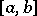, but in the case of spaces 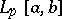all its points belong to the continuous spectrum, and in the case 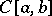they belong to the residual spectrum.

The operator-valued function 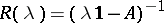defined on 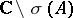is called the resolvent of the linear operator 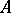. It is useful, particularly because for every function 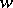, holomorphic in some neighbourhood 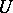of the spectrum, it makes it possible to consider the linear operator (denoted by )

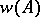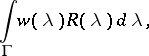where 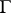is a smooth contour in 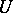that bounds the spectrum. In this way one can construct a "holomorphic operator calculus" ; as for "holomorphic multi-operator calculus" , that is, loosely speaking, giving a reasonable sense to the concept of a holomorphic function of several "operator" variables, the problem of constructing it turned out to be far more difficult. Results that are in a certain sense close to final have been obtained by methods of homological algebra [5].

In the theory of linear operators between Banach spaces an important operation is that of going over from to its so-called adjoint linear operator 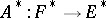(cf. also Adjoint operator), which is defined by the formula

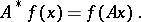This operation has the properties

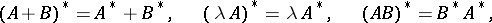(on the assumption that the left-hand sides of the equalities make sense). If and 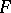are reflexive (cf. Reflexive space), then .

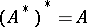Some of the most important classes of linear operators in Banach spaces are the following.

1) 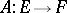is called a compact operator, or a completely-continuous operator, if it maps any bounded set in 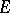to a totally-bounded (that is, pre-compact) set in 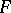. Every linear operator that can be approximated in the operator norm by finite-dimensional (having finite-dimensional image) linear operators is compact. For the overwhelming majority of classical Banach spaces 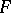the converse is also true: Every compact linear operator from any 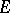to 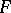can be approximated by finite-dimensional operators. The so-called approximation problem (is this true for all 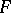?) has been negatively answered [6].

The identity linear operator in 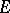is compact if and only if 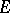is finite dimensional (Riesz' theorem). The spectrum of a compact linear operator is a set containing that is at most countable. If the spectrum is infinite, then is the unique limit point of it. Every 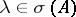, , 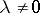is an eigen value, and the eigen vectors corresponding to it form a finite-dimensional space.

2) 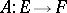is called a nuclear operator if it can be represented as an absolutely convergent series in 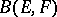consisting of one-dimensional linear operators; such an operator is necessarily compact. By means of nuclear linear operators one can define a class of topological vector spaces, called nuclear spaces, which is important in analysis (cf. Nuclear space).

3) 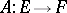is called a Fredholm operator if its kernel and cokernel are finite dimensional; the image of such a linear operator is necessarily closed. The main characteristic of a linear Fredholm operator is its index . The set of linear Fredholm operators is open in 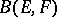and the index on it (in contrast to the dimensions of the kernel and cokernel taken separately) is a locally constant function. The forerunner of the theory of linear Fredholm operators was the theory of integral equations. Set up by E. Fredholm, who essentially proved (and D. Hilbert perceived this "geometrical" background) that a linear operator of the form 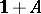with compact 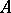is a Fredholm operator and has index zero (see Fredholm alternative). Important specific classes of linear Fredholm operators arise in considering elliptic differential expressions on manifolds. The problem of calculating their index required the apparatus of algebraic topology [8] (cf. also Index formulas).

The problem of classifying endomorphisms of Banach spaces, in view of Jordan's theorem, which gives a finite-dimensional model of its solution, can be treated "to a first approximation" as the problem of constructing an appropriate infinite-dimensional analogue of the Jordan form of a linear operator. However, it is far from being solved: to say nothing about a "sufficient" set of invariant subspaces, it is not known so far (1989) whether every operator that acts on a Hilbert space 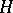has at least one non-trivial (distinct from 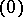and 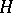) invariant subspace. If a linear operator 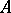that acts on an arbitrary Banach space is not proportional to 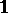and commutes with some compact linear operator, then the set of all linear operators that commute with 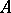is a non-trivial invariant subspace (see [9]).

Apart from the topology of a normed space, there are topologies in 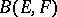that specify the structure of a locally convex space in it. The most important are the strong and weak operator topologies, specified, respectively, by the systems of semi-norms

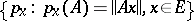and

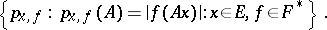The theory of continuous linear operators on topological vector spaces (an example of such a linear operator is the Fourier transform on generalized functions) was developed on the basis of the "Banach" theory. A significant place in it is taken by the investigation of the possibility of generalizing Banach's classical theorems and others; it led to the introduction of a number of important classes of spaces. For example, the theorem on the equivalence of continuity and boundedness, the Banach–Steinhaus theorem and Banach's theorem on the inverse operator are not true for arbitrary, at least locally convex, separable complete spaces. At the same time, the first of these theorems is true if 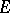is a bornological space, the second if 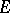is a barrelled space, and the third if 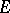is absolutely complete and is a barrelled space.

Continuous linear operators on Hilbert spaces

(finite-dimensional and infinite-dimensional). Their theory was first formalized in the work of Hilbert [10] on integral equations and infinite quadratic forms.

Examples.

1) All examples of linear operators in 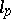, , 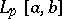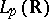considered above, for .

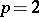2) The integral operator in 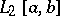that takes 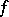to ,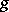

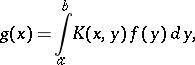where 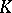is a square-integrable function on the set 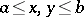. Such a linear operator is always compact.

3) The Fourier operator in 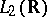is uniquely defined by the fact that it coincides with the classical Fourier operator (see above) on .

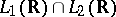The concepts and facts are given below in the form that they have for spaces over 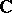: namely, in complex spaces the theory has turned out to be most important and meaningful.

The special position of the "Hilbert" theory of linear operators in the background of the "Banach" theory is determined by the sharply increasing role of the concept of the adjoint operator. Since a Hilbert space 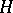and its adjoint 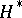are anti-isomorphic, the linear operator 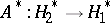is naturally identified with the linear operator from 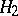to 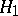uniquely defined by 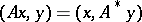, , 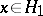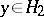; under this identification the linear operator adjoint to an endomorphism in 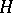again acts 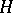in . In 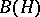there arises an important additional structure — the operation of transition from 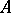to 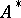, which has involutory properties and with respect to which 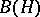is a 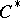-algebra. In fact, every 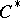-algebra is isometrically -isomorphic to a 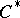-subalgebra of 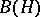for some 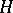(the Gel'fand–Naimark theorem).

The following classes of linear operators are characteristic of Hilbert spaces.

A linear operator 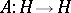is called a self-adjoint operator, or a Hermitian operator, if . A self-adjoint linear operator equal to its square is called a projector (projection operator); such a linear operator can be realized as the operator of orthogonal projection onto a closed subspace of 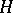. A linear operator 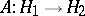is called a unitary operator (in the case of the field 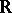, an orthogonal operator) if 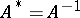, or, equivalently, if , 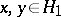and 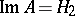. A linear operator is unitary if and only if it is an isomorphism that preserves norms. Self-adjoint and unitary endomorphisms are special cases of a normal operator: A linear operator 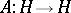such that .

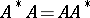The linear operator of multiplication by a sequence (respectively, a function) in 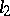(respectively, in 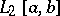) is self-adjoint if and only if this sequence (function) is real valued. A linear integral operator is self-adjoint if and only if almost-everywhere. In 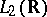shift operators and the Fourier operator are unitary. In 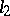the linear operators of left and right shift are adjoint to one another and are not normal. The spectrum of a self-adjoint linear operator lies in , and the spectrum of a unitary operator lies on the unit circle in 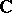. The spectrum of a projector 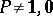consists of the points and . 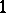The spectrum of a normal linear operator can be any compact set in 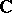. The eigen vectors of a self-adjoint linear operator corresponding to different eigen values are orthogonal.

The classes of linear operators described above are used in a large number of branches of mathematics and physics, including quantum mechanics (where self-adjoint linear operators are interpreted as observables), the theory of representations and harmonic analysis, the theory of differential equations, and the theory of dynamical systems.

All information about a linear operator acting in a finite-dimensional Hilbert space is provided by its matrix notation in an orthogonal basis. In this notation transition to the adjoint linear operator corresponds to taking the matrix that is the complex conjugate of the transposed matrix; as a consequence, for the matrix 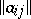of a self-adjoint linear operator one has 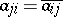. The classical theorem "on reduction to diagonal form" asserts that every normal (in the case of the field , every self-adjoint) linear operator can be written in some orthonormal basis as a diagonal matrix. Together with the fact that linear operators are unitarily equivalent if and only if they can be described (each in its own orthogonal basis) by the same matrices, this theorem implies that the sets of eigen values (taking account of their multiplicity) form a complete system of invariants of unitary equivalence for normal linear operators.

The theorem on reduction to diagonal form turned out to be "happier" than Jordan's theorem in that a meaningful infinite-dimensional analogue was found for it, the spectral theorem for normal linear operators, discovered in 1912: A normal linear operator can be represented uniquely as an operator-valued Stieltjes integral 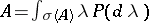, where 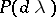is a countably-additive regular (in the sense of the strong operator topology, for example) function on the Borel subsets of 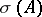that takes values among projectors and is such that 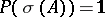(see Spectral measure). A consequence is that every normal linear operator can be approximated by linear combinations of projectors.

On the basis of Hilbert's theorem a complete classification up to unitary equivalence of normal linear operators (in a space of arbitrary dimension) has been obtained [11]; in particular, it turns out that every normal linear operator is unitarily equivalent to the operator of multiplication by a bounded measurable function in 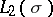, where 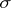is a measurable space with finite measure. For compact normal linear operators in a separable space the picture is simplified: such a linear operator has as orthonormal basis its own eigen vectors and is therefore unitarily equivalent to the operator of multiplication by a sequence acting in 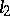(the sequence necessarily converges to zero).

In the case of a normal 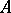the spectral theorem makes it possible to assign a meaning to the function expression 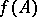for a wider class of functions on the spectrum than holomorphic functions, for example, for a continuous 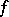the linear operator 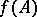is defined as 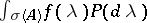. If 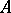is self-adjoint, then the linear operator 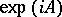is unitary.

The main effort has been concentrated on the study of different classes of non-normal linear operators, in the first place abstract Volterra operators, condensing operators and spectral operators (see [11]–[13], and Volterra operator; Spectral operator; Condensing operator). Although regularities comparable with the regularity in the spectral theorem have still (1989) not been discovered, nevertheless deep results have been obtained in this direction.

The development of analysis and its applications, in the first place differential equations and quantum mechanics, forces one to go beyond the class of bounded (that is, continuous) linear operators. Strictly speaking, an unbounded operator 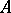in 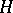is not a linear operator in the sense accepted here, since it is defined not on the whole of 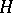, but only on a dense subspace of it, as a rule. Typical examples are the linear operator of multiplication by and differentiation in 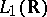. For unbounded linear operators analogues of the spectrum, the adjoint linear operator and the classes of linear operators considered above have been defined. Although their theory is more complicated than the theory of bounded linear operators, a number of deep results of the latter has been generalized meaningfully. The most important of these is an analogue of the spectral theorem, discovered by J. von Neumann for unbounded self-adjoint operators.

References

[1]	G. Peano, "Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann" , Bocca (1888)
[2]	I.M. Gel'fand, "Lectures on linear algebra" , Interscience (1961) (Translated from Russian) Zbl 0098.01108
[3]	O. Toeplitz, "Ueber die Auflösung unendlichvieler linearer Gleichungen mit unendlichvielen Unbekannten" Rend. Circolo Mat. Palermo , 28 (1909) pp. 88–96
[4]	S.S. Banach, "A course of functional analysis" , Kiev (1948) (In Ukrainian)
[5]	J.L. Taylor, "A general framework for a multi-operator functional calculus" Advances in Math. , 9 : 2 (1972) pp. 183–252 MR0328625
[6]	P. Enflo, "A counterexample to the approximation problem in Banach spaces" Acta Math. , 130 (1973) pp. 309–317 MR0402468 Zbl 0267.46012
[7]	H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) MR0193469 Zbl 0141.30503
[8]	, Functional analysis , Math. Reference Library , Moscow (1972) (In Russian)
[9]	V.I. Lomonosov, "Invariant subspaces of a family of operators that commute with a completely continuous operator" Funktsional. Anal. i Prilozhen. , 3 (1973) pp. 55–56 (In Russian) MR420305
[10]	D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) MR0056184 Zbl 0050.10201
[11]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523
[12]	N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) MR0188745
[13]	N. Dunford, J.T. Schwartz, "Linear operators. Spectral operators" , 3 , Interscience (1971) MR0412888
[14]	I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Theory and applications of Volterra operators in Hilbert space" , Amer. Math. Soc. (1970) (Translated from Russian) MR0264447 Zbl 0194.43804
[15]	B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) (Translated from French) MR275190
[16]	N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) MR2333539 MR2327161 MR2325344 MR2284892 MR2272929 MR0928386 MR0896478 MR0782297 MR0782296 MR0722608 MR0682756 MR0643362 MR0647314 MR0610795 MR0583191 MR0354207 MR0360549 MR0237342 MR0205211 MR0205210

Comments

For a fairly recent text on multi-dimensional functional calculus cf. [a6].

References

[a1]	I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1977) MR1843182 MR0632943 Zbl 0990.47001 Zbl 0458.47001
[a2]	I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) MR0246142 Zbl 0181.13504
[a3]	P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958) MR0089819 Zbl 0107.01404
[a4]	A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) MR0710486 Zbl 0516.47023
[a5]	C. Pearcy (ed.) , Topics in operator theory , Amer. Math. Soc. (1974) MR0350446 Zbl 0291.00011
[a6]	F.H. Vasilescu, "Analytic functional calculus and spectral decompositions" , Reidel (1982) MR0690957 Zbl 0495.47013