Kustaanheimo-Stiefel transformation
A particular case of the surjective application $ \mathbf R ^ {4} \rightarrow \mathbf R ^ {3} : ( u _ {0} ,u _ {1} ,u _ {2} ,u _ {3} ) \mapsto ( x _ {0} ,x _ {2} ,x _ {3} ) $
defined by
$$ \tag{a1 } \left . \begin{array}{c} x _ {0} = u _ {0} ^ {2} - p u _ {1} ^ {2} + q u _ {2} ^ {2} - pq u _ {3} ^ {2} , \\ x _ {2} = 2 ( u _ {0} u _ {2} + p u _ {1} u _ {3} ) , \\ x _ {3} = 2 ( u _ {0} u _ {3} + u _ {1} u _ {2} ) , \\ \end{array} \right \} $$
subject to the constraint $ \omega = 0 $ with
$$ \tag{a2 } \omega = 2 ( u _ {1} du _ {0} - u _ {0} du _ {1} + q u _ {3} du _ {2} - q u _ {2} du _ {3} ) , $$
where the parameters $ p $ and $ q $ can take the values $ \pm 1 $. The transformation introduced by P. Kustaanheimo and E. Stiefel [a1] corresponds to $ p = q = - 1 $, while the cases $ p = - q = - 1 $[a2] and $ p = - q = 1 $( or $ p = q = 1 $) [a3] correspond to two other (inequivalent) transformations.
There are several ways of introducing these three transformations. For instance, the Kustaanheimo–Stiefel mapping is inherent to the Cartan spinor theory, since (a1), with $ p = q = - 1 $, can be rewritten as $ x _ {0} = \xi ^ \dag \sigma _ {3} \xi $, $ x _ {2} = \xi ^ \dag \sigma _ {1} \xi $ and $ x _ {3} = \xi ^ \dag \sigma _ {2} \xi $, where the $ \sigma _ {i} $( with $ i = 1,2,3 $) are the Pauli matrices and $ \xi $ is a spinor of components $ u _ {0} - i u _ {1} $ and $ u _ {2} + i u _ {3} $( $ \xi ^ \dag $ stands for the adjoint of $ \xi $). Furthermore, the Kustaanheimo–Stiefel transformation, along with the two other transformations, can be introduced as a particular Hurwitz transformation (see also Hurwitz transformation) in the framework of the Cayley–Dickson algebra $ A ( p,q ) $. (The algebra $ A ( p,q ) $ turns out to be the algebra of ordinary (or elliptic) quaternions when $ p + q = - 2 $ and the algebra of hyperbolic quaternions when $ p + q \neq - 2 $.) The main properties of the transformations (a1)–(a2) are as follows.
1) These transformations satisfy
$$ dx _ {0} ^ {2} - q dx _ {2} ^ {2} + pq dx _ {3} ^ {2} = 4 r ( {} ^ {\textrm{ t } } d \mathbf u \eta d \mathbf u ) $$
and
$$ \tag{a3 } x _ {0} ^ {2} - q x _ {2} ^ {2} + pq x _ {3} ^ {2} = r ^ {2} , $$
where the metric $ \eta $ is $ \eta = { \mathop{\rm diag} } ( 1, - p, - q, pq ) $, so that
$$ \tag{a4 } r = ( {} ^ {\textrm{ t } } \mathbf u \eta \mathbf u ) = u _ {0} ^ {2} - p u _ {1} ^ {2} - q u _ {2} ^ {2} + pq u _ {3} ^ {2} $$
( $ \mathbf u $ denotes a column vector, the transposed of which is the row vector $ {} ^ {\textrm{ t } } \mathbf u = ( u _ {0} , u _ {1} , u _ {2} , u _ {3} ) $).
2) Equations (a3)–(a4) show that the various mappings (a1) correspond to three types of fibrations (cf. Fibration): the celebrated Hopf fibration (on spheres) $ \mathbf S ^ {3} \rightarrow \mathbf S ^ {2} $ of compact fibre $ \mathbf S ^ {1} $ for $ p = q = - 1 $ and two other fibrations (on hyperboloids), namely, $ \mathbf R ^ {2} \times \mathbf S ^ {1} \rightarrow \mathbf R ^ {2} $ of compact fibre $ \mathbf S ^ {1} $ for $ p = - q = - 1 $ and $ \mathbf R ^ {2} \times \mathbf S ^ {1} \rightarrow \mathbf R \times \mathbf S ^ {1} $ of non-compact fibre $ \mathbf R $ for $ p = - q = 1 $ and $ p = q = 1 $.
3) The preceding geometrical property can be made precise by transformation properties of (first- and) second-order elliptic and hyperbolic differential operators. For example, this yields (for $ f \in C ^ {2} ( \mathbf R ^ {3} ) $)
$$ \Delta _ {x} f = { \frac{1}{4r } } \Delta _ {u} f, Xf = 0, $$
where
$$ \Delta _ {x} = \partial _ {x _ {0} x _ {0} } - q \partial _ {x _ {2} x _ {2} } + pq \partial _ {x _ {3} x _ {3} } , $$
$$ \Delta _ {u} = \partial _ {u _ {0} u _ {0} } - p \partial _ {u _ {1} u _ {1} } - q \partial _ {u _ {2} u _ {2} } + pq \partial _ {u _ {3} u _ {3} } , $$
$$ X = - p u _ {1} \partial _ {u _ {0} } - u _ {0} \partial _ {u _ {1} } + p u _ {3} \partial _ {u _ {2} } + u _ {2} \partial _ {u _ {3} } . $$
4) The vector field $ X $ associated to the $ 1 $- form $ \omega $( with an action satisfying $ \omega [ {1 / {( 4r ) } } X ] = 1 $) is an element of the symplectic Lie algebra $ { \mathop{\rm sp} } ( 8, \mathbf R ) $ which generates either the subalgebra $ { \mathop{\rm so} } ( 2 ) $ or $ { \mathop{\rm so} } ( 1,1 ) $, according to whether the fibre is compact or non-compact. The introduction of the (Dirac primary) constraint $ X = 0 $ in $ { \mathop{\rm sp} } ( 8, \mathbf R ) $ produces a Lie algebra under constraint (i.e., the centralizer of $ X $ in $ { \mathop{\rm sp} } ( 8, \mathbf R ) $), which is isomorphic to $ { \mathop{\rm so} } ( 4,2 ) $ or $ { \mathop{\rm so} } ( 3,3 ) $, depending on the compactness or non-compactness of the fibre, respectively (see [a3] and the references therein).
The applications of the transformations (a1)–(a2) range from number theory to physics (classical and quantum mechanics, gauge theories). By way of illustration, the (generalized) Hurwitz matrix corresponding to (a1)–(a2) is connected to the (generalized) problem of factoring the sum of four squared numbers, addressed by A. Hurwitz (1898) in the specific case $ p = q = - 1 $. In addition, for $ p $ and $ q $ fixed, the solutions of the generalized Pythagorean equation (a3) with $ ( x _ {0} , x _ {1} , x _ {2} , r ) \in \mathbf Z ^ {4} $ are parametrized by (a1) and (a4) with $ ( u _ {0} ,u _ {1} , u _ {2} , u _ {3} ) \in \mathbf Z ^ {4} $. In classical mechanics, the Kustaanheimo–Stiefel transformation is used for the regularization of the Kepler problem. In quantum mechanics (cf. also MIC-Kepler problem), the latter transformation makes it possible to transform the Schrödinger equation for the three-dimensional hydrogen atom (in an electromagnetic field) into a Schrödinger equation for a four-dimensional isotropic harmonic oscillator (with quartic and sextic anharmonic terms) subject to a constraint [a4], [a5]. Conversely, the mappings (a1)–(a2) may be used in some dimensional reduction process for converting a dynamical system in $ \mathbf R ^ {4} $ or $ \mathbf R ^ {2} \times \mathbf R ^ {2} $ into a dynamical system in $ \mathbf R ^ {3} $.
References
| [a1] | P. Kustaanheimo, E. Stiefel, "Perturbation theory of Kepler motion based on spinor regularization" J. Reine Angew. Math. , 218 (1965) pp. 204 |
| [a2] | T. Iwai, "On reduction of two degrees of freedom Hamiltonian system by an 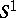 action, and action, and 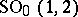 as a dynamical group" J. Math. Phys. , 26 (1985) pp. 885 as a dynamical group" J. Math. Phys. , 26 (1985) pp. 885 |
| [a3] | D. Lambert, M. Kibler, "An algebraic and geometric approach to non-bijective quadratic transformations" J. Phys. A: Math. Gen. , 21 (1988) pp. 307 |
| [a4] | M. Boiteux, "Theory of nonbijective canonical transformations in mechanics: Application to the Coulomb problem" J. Math. Phys. , 23 (1982) pp. 1311 |
| [a5] | M. Kibler, T. Négadi, "Hydrogen atom in a uniform electromagnetic field as an anharmonic oscillator" Lett. Nuovo Cim. , 39 (1984) pp. 319 |
Kustaanheimo-Stiefel transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kustaanheimo-Stiefel_transformation&oldid=47538