Inverse trigonometric functions
inverse circular functions
Functions inverse to the trigonometric functions. The six basic trigonometric functions correspond to the six inverse trigonometric functions. These are called arcussine, arcuscosine, arcustangent, arcuscotangent, arcussecant, arcuscosecant, and are denoted, respectively, by $ { \mathop{\rm Arc} \sin } x $, $ { \mathop{\rm Arc} \cos } x $, $ { \mathop{\rm Arc} \mathop{\rm tan} } x $, $ { \mathop{\rm Arc} \mathop{\rm cotan} } x $, $ { \mathop{\rm Arc} \mathop{\rm sec} } x $, $ { \mathop{\rm Arc} \cosec } x $. The functions $ { \mathop{\rm Arc} \sin } x $ and $ { \mathop{\rm Arc} \cos } x $ are defined (in the real domain) for $ | x | \leq 1 $; $ { \mathop{\rm Arc} \mathop{\rm tan} } x $ and $ { \mathop{\rm Arc} \mathop{\rm cotan} } x $ for all real $ x $; $ { \mathop{\rm Arc} \mathop{\rm sec} } x $ and $ { \mathop{\rm Arc} \cosec } x $ for $ | x | \geq 1 $; the last two functions are seldom used. Other notations are $ \sin ^ {-} 1 x $, $ \cos ^ {-} 1 x $, etc.
Since the trigonometric functions are periodic, their inverses are many-valued. The single-valued branches (principal branches) of these functions are denoted by $ { \mathop{\rm arc} \sin } x $, $ { \mathop{\rm arc} \cos } x ,\dots $. Namely, $ { \mathop{\rm arc} \sin } x $ is the branch of $ { \mathop{\rm Arc} \sin } x $ for which $ - \pi / 2 \leq { \mathop{\rm arc} \sin } x \leq \pi / 2 $. Similarly, $ { \mathop{\rm arc} \cos } x $, $ { \mathop{\rm arc} \mathop{\rm tan} } x $ and $ { \mathop{\rm arc} \mathop{\rm cotan} } x $ are defined by the conditions $ 0 \leq { \mathop{\rm arc} \cos } x \leq \pi $, $ - \pi / 2 \leq { \mathop{\rm arc} \mathop{\rm tan} } x \leq \pi / 2 $, $ 0 < { \mathop{\rm arc} \mathop{\rm cotan} } x < \pi $.
The figures show the graphs of $ y = { \mathop{\rm Arc} \sin } x $, $ y = { \mathop{\rm Arc} \cos } x $, $ y = { \mathop{\rm Arc} \mathop{\rm tan} } x $, $ y = { \mathop{\rm Arc} \mathop{\rm cotan} } x $; the principal branches are distinguished by a heavy line.
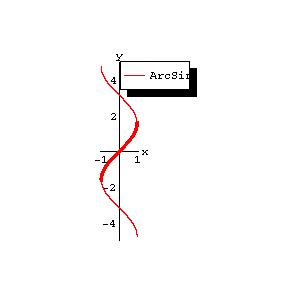
Figure: i052410a
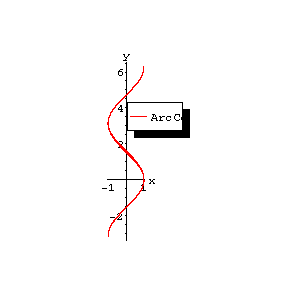
Figure: i052410b
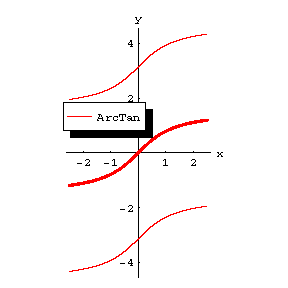
Figure: i052410c
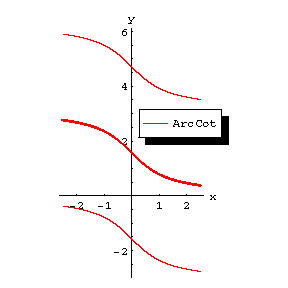
Figure: i052410d
The functions $ { \mathop{\rm Arc} \sin } x \dots $ are easily expressed in terms of $ { \mathop{\rm arc} \sin } x \dots $ for example:
$$ { \mathop{\rm Arc} \sin } x = \ ( - 1 ) ^ {n} { \mathop{\rm arc} \sin } x + \pi n , $$
$$ { \mathop{\rm Arc} \cos } x = \ \pm { \mathop{\rm arc} \cos } x + 2 \pi n , $$
$$ { \mathop{\rm Arc} \mathop{\rm tan} } x = { \mathop{\rm arc} \mathop{\rm tan} } x + \pi n , $$
$$ { \mathop{\rm Arc} \mathop{\rm cotan} } x = { \mathop{\rm arc} \mathop{\rm cotan} } x + \pi n , $$
$$ n = 0 , \pm 1 ,\dots . $$
The inverse trigonometric functions are related by
$$ { \mathop{\rm arc} \sin } x + { \mathop{\rm arc} \cos } x = \ \frac \pi {2} ,\ \ - 1 \leq x \leq 1 , $$
$$ { \mathop{\rm arc} \mathop{\rm tan} } x + { \mathop{\rm arc} \mathop{\rm cotan} } x = \frac \pi {2} ,\ - \infty < x < + \infty . $$
Hence $ { \mathop{\rm arc} \cos } x $ and $ { \mathop{\rm arc} \mathop{\rm cotan} } x $ are not included in the following formulas.
The inverse trigonometric functions are infinitely differentiable and can be expanded in a series in a neighbourhood of any interior point of their domain of definition. The derivatives, integrals and series expansions are:
$$ ( { \mathop{\rm arc} \sin } x ) ^ \prime = \ \frac{1}{\sqrt {1 - x ^ {2} } } ,\ \ ( { \mathop{\rm arc} \mathop{\rm tan} } x ) ^ \prime = \ \frac{1}{1 + x ^ {2} } , $$
$$ \int\limits { \mathop{\rm arc} \sin } x d x = x { \mathop{\rm arc} \sin } x + \sqrt {1 - x ^ {2} } + C , $$
$$ \int\limits { \mathop{\rm arc} \mathop{\rm tan} } x d x = x { \mathop{\rm arc} \mathop{\rm tan} } x - \frac{1}{2} \mathop{\rm ln} ( 1 + x ^ {2} ) + C , $$
$$ { \mathop{\rm arc} \sin } x = x + \sum _ { n= } 1 ^ \infty \frac{ ( 2 n - 1 ) !! }{( 2 n ) !! } \frac{x ^ {2n+} 1 }{2 n + 1 } ,\ | x | < 1 , $$
$$ { \mathop{\rm arc} \mathop{\rm tan} } x = \sum _ { n= } 0 ^ \infty \frac{( - 1 ) ^ {n} }{2 n + 1 } x ^ {2n+} 1 ,\ | x | < 1 . $$
The inverse trigonometric functions of a complex variable are defined as the analytic continuations to the complex plane of the corresponding real functions.
The inverse trigonometric functions can be expressed in terms of the logarithmic function:
$$ { \mathop{\rm arc} \sin } z = - i \mathop{\rm ln} ( i z + \sqrt {1 - z ^ {2} } ) , $$
$$ { \mathop{\rm arc} \cos } z = - i \mathop{\rm ln} ( z + \sqrt {z ^ {2} - 1 } ) , $$
$$ { \mathop{\rm arc} \mathop{\rm tan} } z = - \frac{i}{2} \mathop{\rm ln} \frac{1 + i z }{1 - i z } , $$
$$ { \mathop{\rm arc} \mathop{\rm cotan} } z = - \frac{i}{2} \mathop{\rm ln} \frac{i z - 1 }{i z + 1 } . $$
Comments
Other notations for $ \mathop{\rm tan} ^ {-} 1 x $ and $ \mathop{\rm cotan} ^ {-} 1 x $ are $ \mathop{\rm tg} ^ {-} 1 x $ and $ \mathop{\rm ctg} ^ {-} 1 x $, respectively.
References
| [a1] | M.R. Spiegel, "Complex variables" , Schaum's Outline Series , McGraw-Hill (1974) |
| [a2] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) |
Inverse trigonometric functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_trigonometric_functions&oldid=47423