Information distance
A metric or pseudo-metric on the set of probability distributions, characterizing the "non-similarity" of the random phenomena described by these distributions. Most interesting is the information distance $ \rho ( P, Q ) $
related to the measure of informativity of an experiment in the problem of differentiating between $ P $
and $ Q $
by observations.
In any concrete statistical problem it is necessary to make inferences on the observed phenomenon. These inferences are, as a rule, not exact, since the outcomes of observations are random. It is intuitively clear that any sample carries some amount of useful information. Moreover: A) information may only get lost in transmission; and B) information presented by different independent sources, e.g. independent samples, can be summed. Thus, if one introduces the informativity of an experiment as the average amount of information (cf. also Information, amount of) in an observation, then for it the axioms A) and B) are fulfilled. Although the concept of information remains intuitive, one can sometimes find a quantity $ I $ satisfying A) and B) that describes asymptotically the average exactness of inferences in a problem with a growing number of observations, and that therefore can naturally be taken as the informativity. The informativity is either a numerical or a matrix quantity. An important example is the information matrix in the problem of estimating the parameter of a distribution law.
According to axiom B) informativities behave like squares of length, i.e. the square of a reasonable information distance must have the property of additivity. The simplest information distances are: the distance in variation:
$$ \rho _ {V} ( P , Q ) = \ \int\limits | P ( d \omega ) - Q ( d \omega ) | , $$
and the Fisher distance in an invariant Riemannian metric:
$$ \rho _ {F} ( P , Q ) = \ 2 { \mathop{\rm arc} \cos } \int\limits \sqrt {P ( d \omega ) Q ( d \omega ) } . $$
The latter does not have the property of additivity, and has no proper statistical meaning.
According to the Neyman–Pearson theory all the useful information about differentiating between probability distributions $ P ( d \omega ) $ and $ Q ( d \omega ) $ on a common space $ \Omega $ of outcomes $ \omega $ is contained in the likelihood ratio or its logarithm:
$$ \mathop{\rm ln} p ( \omega ) - \mathop{\rm ln} q ( \omega ) = \ \mathop{\rm ln} \frac{d P }{d Q } ( \omega ) , $$
determined up to values on a set of outcomes of probability zero. The mathematical expectation
$$ I ( P : Q ) = \ \int\limits _ \Omega \left [ \mathop{\rm ln} \ \frac{p ( \omega ) }{q ( \omega ) } \right ] \ P ( d \omega ) = $$
$$ = \ \int\limits _ \Omega \left [ \frac{P ( d \omega ) }{Q ( d \omega ) } \mathop{\rm ln} \frac{P ( d \omega ) }{Q ( d \omega ) } \right ] Q ( d \omega ) $$
is called the (average) information for differentiating (according to Kullback) in favour of $ P $ against $ Q $, and also the relative entropy, or information deviation. The non-negative (perhaps infinite) quantity $ I ( P : Q ) $ satisfies axioms A) and B). It characterizes the exactness of one-sided differentiation of $ P $ against $ Q $, having defined the maximal order of decrease of the probability $ \beta _ {N} $ of an error of the second kind (i.e. falsely accepting hypothesis $ P $ when it is not true). As the number $ N $ of independent observations grows one has:
$$ \beta _ {N} \sim e ^ {- N \cdot I ( P : Q ) } , $$
for a fixed significance level — the probability $ \alpha _ {N} $ of an error of the first kind, $ 0 < \alpha _ {0} \leq \alpha _ {N} \leq \alpha _ {1} < 1 $.
The analogous quantity $ I ( Q : P ) $ determines the maximal order of decrease of $ \alpha _ {N} $ for $ 0 < b _ {0} \leq \beta _ {N} \leq b _ {1} < 1 $. The relation of "similarity" , in particular that of "similarity" of random phenomena, is not symmetric and, as a rule, $ I ( P : Q ) \neq I ( Q : P) $. The geometric interpretation of $ I ( P : Q ) $ as half the square of the non-symmetric distance from $ Q $ to $ P $ proved to be natural in a number of problems in statistics. For such information distances the triangle inequality is not true, but a non-symmetric analogue of the Pythagorean theorem holds:
$$ I ( R : P ) = I ( R : Q ) + I ( Q : P ) , $$
if
$$ \int\limits _ \Omega \left [ \mathop{\rm ln} \ \frac{q ( \omega ) }{p ( \omega ) } \right ] Q ( d \omega ) = \ \int\limits _ \Omega \left [ \mathop{\rm ln} \ \frac{q ( \omega ) }{p ( \omega ) } \right ] \ R ( d \omega ) . $$
A symmetric characteristic of similarity of $ P $ and $ Q $ arises when testing them by a minimax procedure. For an optimal test
$$ \alpha _ {N} = \beta _ {N} \sim e ^ {- N I _ {PQ} } , $$
$$ I _ {PQ} = - \mathop{\rm ln} \min _ {0 < u < 1 } \int\limits _ \Omega | P ( d \omega ) | ^ {u} | Q ( d \omega ) | ^ {1-} u = $$
$$ = \ \min _ { R } \max \{ I ( R : P ) , I ( R : Q ) \} . $$
Certain other information distances are related to the information deviation (cf. [1], [2]). For infinitesimally close $ P $ and $ Q $ the principal part of the information deviation, as well of the square of any reasonable information distance, is given, up to a constant multiple $ c ( I) $, by the Fisher quadratic form. For the information deviation
$$ c ( I) = \frac{1}{2} . $$
On the other hand, any information deviation satisfying axiom A) only induces a topology which majorizes the topology induced by the distance in variation (defined above), [3], [4].
References
| [1] | S. Kullback, "Information theory and statistics" , Wiley (1959) |
| [2] | N.N. [N.N. Chentsov] Čentsov, "Statistical decision rules and optimal inference" , Amer. Math. Soc. (1982) (Translated from Russian) |
| [3] | I. Csiszar, "On topological properties of 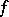 -divergences" Studia Sci. Math. Hungar. , 2 (1967) pp. 329–339 -divergences" Studia Sci. Math. Hungar. , 2 (1967) pp. 329–339 |
| [4] | E.A. Morozova, N.N. [N.N. Chentsov] Čencov, "Markov maps in noncommutative probability theory and mathematical statistics" Yu.V. Prokhorov (ed.) et al. (ed.) , Probability theory and mathematical statistics , VNU (1987) pp. 287–310 |
Information distance. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Information_distance&oldid=47356