Hypergroups, harmonic analysis on locally compact
Locally compact hypergroups are natural generalizations of locally compact group measure algebras; the field is therefore part of the research programme designed under "harmonic analysis without a group to do it on" (cf. also Harmonic analysis; Harmonic analysis, abstract; for the notion of a hypergroup, see also Generalized displacement operators). The idea goes back to I.M. Gel'fand, A. Povzner and B. Levitan [a14] on the one hand, and to J. Delsarte [a4] on the other. Another approach has been undertaken by Yu. Berezanskii and collaborators [a1].
For fundamentals and examples, as well as results oriented towards probability theory, see [a2]. It contains an almost complete and up-to-date (1996) bibliography.
Haar measure.
Basic results from [a5] prove the existence and uniqueness of the Haar measure for locally compact commutative hypergroups as well as for discrete hypergroups. The compact case has been settled independently and in a different way in [a13], which imitates a construction by A. Weil. In the non-compact case, Spector's proof involves a deep new fixed-point theorem for not necessarily affine mappings preserving a compact convex subset in a locally convex vector space.
The problem of whether the Haar measure exists on a locally compact hypergroup is still open, but an important step towards a complete answer is given by using a generalization of the Ryll–Nardzewski fixed-point theorem [a7], embodying Spector's theorem.
Commutative locally compact hypergroups.
The basic facts about the Plancherel measure (cf. also Plancherel formula) are presented in [a3].
It is shown in [a8] that the general $ L _ {2} $- theory appears as a consequence of the Plancherel–Godement theory for an involutive algebra.
A crucial issue is to decide which (commutative) locally compact hypergroups possess a Fourier–Eymard algebra. The question is widely open for further research; notably, an elementary finite counterexample is provided in [a13].
The compact case.
Whilst the $ L _ {2} $- theory appears as generalizing known facts for compact commutative groups (at least at first glance), the $ L _ {1} $- theory proves to be extremely involved and deep. R. Vrem proved [a6] the crucial property allowing one to work with trigonometric polynomials: this subspace is dense in $ L _ {1} $. Vrem's approach makes strong use of the compact group case and does not allow further generalizations.
A radically new approach was provided in [a8], which showed the existence of a universal, and explicit, bounded approximate identity comprising trigonometric polynomials, using the Dixmier symbolic calculus [a5].
The latter result allows one to develop basic definitions of Sidon sets (in the classical sense) in full generality (cf. also Harmonic analysis, abstract). Pioneering work related to that question was performed in [a17]. The question here is to decide which class of commutative compact hypergroups do possess non-trivial Sidon sets. See [a2], [a9]. The problem seems to be related to the symmetry (or non-symmetry) of the associated measure algebra, an extremely deep problem.
The general case.
One basic approach is given in [a8]: it relies deeply upon the exploitation of Dixmier's symbolic calculus. An important guideline is to obtain insight into the spectral picture of $ L _ {1} $ by taking care of the growth of the hypergroup. Basic spectral synthesis results are obtained in that way, generalizing the Abelian locally compact group case as well as preliminary results [a3].
Notably, amenability plays a crucial role (quite unexpectedly; cf. Invariant average). The theory is essentially different from the locally compact group situation (even for the commutative theory). A crucial question is to be able to formulate an appropriate Fölner property.
Discrete hypergroups.
The basic axioms are elementary. Aside from commutative examples associated with trees, very little has been accomplished so far (1996). Amenability is again a crucial question: some results have been obtained in [a10] and [a11].
Very important is the fact that discrete hypergroups need not be unimodular [a18]. P.G.A. Floris and T.H. Koornwinder have found connections between quantum groups and discrete hypergroups (cf. also Quantum groups). A remarkable example is provided in [a6]: this example (based on $ q $- Jacobi polynomials) is non-unimodular, GCR, hence type-I; one may compare this example with the relevant result for discrete groups: E. Thoma proved that a discrete group is type-I if and only if it is a finite extension of a commutative discrete group.
References
| [a1] | Yu. Berezanskii, "Hypercomplex systems with a discrete basis" Dokl. Akad. Nauk SSSR (N.S.) , 81 (1954) pp. 825–828 (In Russian) |
| [a2] | W.R. Bloom, H. Heyer, "Harmonic analysis of probability measures on hypergroups" , Studies in Mathematics , 20 , W. de Gruyter (1995) |
| [a3] | A. Chilana, K. Ross, "Spectral synthesis in hypergroups" Pacific J. Math. , 76 (1978) pp. 313–328 |
| [a4] | J. Delsarte, "Hypergroupes et opérateurs de permutation et de transmutation" , La théorie des équations aux dérivées partielles (Nancy, 9–15 avril 1956) , Colloq. CNRS , 71 , CNRS (1956) pp. 29–45 |
| [a5] | J. Dixmier, "Opérateurs de rang fini dans les représentation unitaires" IHES Publ. Math. (1960) pp. 305–317 |
| [a6] | P. Floris, "On quantum groups, hypergroups and 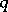 -special functions" Ph.D. Thesis RU Leiden (1995) -special functions" Ph.D. Thesis RU Leiden (1995) |
| [a7] | M.O. Gebuhrer, "The Haar measure on a locally compact hypergroup" Pr. Komrakov (ed.) Pr. Litvinov (ed.) , Proc. Conf. Differential Geometry on Homogeneous Spaces and Harmonic Analysis on Lie Groups (Moscow, 1994) , Kluwer Acad. Publ. (1996) |
| [a8] | M.O. Gebuhrer, "Analyse harmonique sur les espaces de Gel'fand–Levitan et applications à la théorie des semigroupes de convolution" Thæse de doctorat d'etat Univ. Louis Pasteur, Strasbourg (1989) |
| [a9] | M.O. Gebuhrer, "About the fine structure of compact commutative hypergroups" , Preprint , IRMA , Strasbourg (1996) |
| [a10] | M.O. Gebuhrer, "Remarks on amenability of discrete hypergroups" M.A. Picardello (ed.) , Harmonic Analysis and Discrete Potential Theory , Plenum (1992) pp. 479–482 |
| [a11] | M.O. Gebuhrer, A. Kumar, "The Wiener property for a class of discrete hypergroups" Math. Z. , 202 (1989) pp. 271–274 |
| [a12] | M.O. Gebuhrer, A.L. Schwartz, "Sidon sets and Riesz sets on the disk algebra" Colloq. Math. (1996) |
| [a13] | R.I. Jewett, "Spaces with an abstract convolution of measures" Adv. in Math. , 18 (1975) pp. 1–101 |
| [a14] | B. Levitan, A. Povzner, "Differential equations of the Sturm–Liouville type on the semi-axis and Plancherel's theorem" Dokl. Akad. Nauk SSSR (N.S.) , 52 (1946) pp. 479–482 (In Russian) |
| [a15] | R. Spector, "Mesures invariantes sur les hypergroupes" Trans. Amer. Math. Soc. , 239 (1978) pp. 147–165 |
| [a16] | R. Vrem, "Harmonic analysis on compact hypergroups" Pacific J. Math. , 85 (1979) pp. 239–251 |
| [a17] | R. Vrem, "Lacunarity on compact hypergroups" Math. Z. , 164 (1968) pp. 13–104 |
| [a18] | W. Woess, V. Kaimanovitch, "Construction of discrete non-unimodular hypergroups" , Preprint Quaderno : 9 , Univ. Milano (1995) |
Hypergroups, harmonic analysis on locally compact. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypergroups,_harmonic_analysis_on_locally_compact&oldid=47301