Hypergeometric function
A solution of a hypergeometric equation
$$ \tag{1 } z ( 1 - z) w ^ {\prime\prime} + [ \gamma - ( \alpha + \beta + 1) z] w ^ \prime - \alpha \beta w = 0. $$
A hypergeometric function can be defined with the aid of the so-called Gauss series
$$ \tag{2 } F ( \alpha , \beta ; \gamma ; z) = \ {} _ {2} F _ {1} ( \alpha , \beta ; \gamma ; z) = \ F ( \beta , \alpha ; \gamma ; z) = $$
$$ = \ \sum _ {n = 0 } ^ \infty \frac{( \alpha ) _ {n} ( \beta ) _ {n} }{( \gamma ) _ {n} } \frac{z ^ {n} }{n!\ } = $$
$$ = \ \frac{\Gamma ( \gamma ) }{\Gamma ( \alpha ) \Gamma ( \beta ) } \sum _ {n = 0 } ^ \infty \frac{\Gamma ( \alpha + n) \Gamma ( \beta + n) }{\Gamma ( \gamma + n) } \frac{z ^ {n} }{n!} , $$
where $ \alpha , \beta , \gamma $ are parameters which assume arbitrary real or complex values except for $ \gamma = 0, - 1, - 2 ,\dots $; $ z $ is a complex variable; and $ ( x) _ {n} \equiv x( x + 1) \dots ( x + n - 1) $. The function $ F( \alpha , \beta ; \gamma ; z) $ is called a hypergeometric function of the first kind. The second linearly independent solution of (1),
$$ \Phi ( \alpha , \beta ; \gamma ; z) = $$
$$ = \ \frac{\Gamma ( \alpha - \gamma + 1) \Gamma ( \beta - \gamma + 1) }{\Gamma ( \alpha ) \Gamma ( \beta ) \Gamma ( 1 - \gamma ) } z ^ {1 - \gamma } F ( \alpha - \gamma + 1, \beta - \gamma + 1; 2 - \gamma ; z), $$
is called a hypergeometric function of the second kind.
The series (2) is absolutely and uniformly convergent if $ | z | < 1 $; the convergence also extends over the unit circle if $ \mathop{\rm Re} ( \alpha + \beta - \gamma ) < 0 $; if $ 0 \leq \mathop{\rm Re} ( \alpha + \beta - \gamma ) < 1 $ it converges at all points of the unit circle except $ z = 1 $. However, there exists an analytic continuation of the hypergeometric function (2) to the exterior $ | z | > 1 $ of the unit disc with the slit $ ( 1, \infty ) $[1]. The function $ F ( \alpha , \beta ; \gamma ; z ) $ is a univalent analytic function in the complex $ z $-plane with slit $ ( 1, \infty ) $. If $ \alpha $ or $ \beta $ are zero or negative integers, the series (2) terminates after a finite number of terms, and the hypergeometric function is a polynomial in $ z $.
If $ \gamma = - n $, $ n = 0, 1, \dots $ the hypergeometric function is not defined, but
$$ \lim\limits _ {\gamma \rightarrow - n } \ \frac{F ( \alpha , \beta ; \gamma ; z) }{F ( \gamma ) } = $$
$$ = \ \frac{( \alpha ) _ {n + 1 } ( \beta ) _ {n + 1 } }{( n + 1)! } z ^ {n + 1 } F ( \alpha + n + 1, \beta + n + 1; n + 2; z). $$
Elementary relations. The six functions
$$ F ( \alpha \pm 1, \beta ; \gamma ; z),\ \ F ( \alpha , \beta \pm 1; \gamma ; z) \ \ F ( \alpha , \beta ; \gamma \pm 1; z) $$
are said to be contiguous to the hypergeometric function $ F ( \alpha , \beta ; \gamma ; z ) $. There exists a linear relationship between that function and any two functions which are contiguous to it. For instance, C.F. Gauss [2], [3] was the first to find 15 formulas of the type
$$ \gamma F ( \alpha , \beta - 1; \gamma ; z) + ( \alpha - \beta ) zF ( \alpha , \beta ; \gamma + 1; z) = $$
$$ = \ \gamma F ( \alpha - 1, \beta ; \gamma ; z). $$
The associated functions $ F ( \alpha + m , \beta + n ; \gamma + l ; z) $, where $ m, n, l $ are integers, can be obtained by iterated application of Gauss' relations. The following differentiation formulas apply:
$$ \frac{d ^ {n} }{dz ^ {n} } F ( \alpha , \beta ; \gamma ; z) = \ \frac{( \alpha ) _ {n} ( \beta ) _ {n} }{( \gamma ) _ {n} } F ( \alpha + n, \beta + n; \gamma + n; z). $$
Equation (1) has 24 solutions of the form
$$ z ^ \rho ( 1 - z) ^ \sigma F ( \alpha ^ \prime , \beta ^ \prime ; \gamma ^ \prime ; z ^ \prime ), $$
where $ \rho $, $ \sigma $, $ \alpha ^ \prime $, $ \beta ^ \prime $, and $ \gamma ^ \prime $ are linear functions of $ \alpha $, $ \beta $ and $ \gamma $; and $ z $ and $ z ^ \prime $ are connected by a bilinear transformation. Any three solutions are linearly dependent [2]. There exist square, cubic and higher-order transformations [2]–[5].
Principal integral representations. If $ \mathop{\rm Re} \gamma > \mathop{\rm Re} \beta > 0 $ and $ | \mathop{\rm arg} ( 1 - x) | < \pi $, Euler's formula
$$ \tag{3 } F ( \alpha , \beta ; \gamma ; z) = $$
$$ = \ \frac{\Gamma ( \gamma ) }{\Gamma ( \beta ) \Gamma ( \gamma - \beta ) } \int\limits _ { 0 } ^ { 1 } t ^ {\beta - 1 } ( 1 - t) ^ {\gamma - \beta - 1 } ( 1 - tz) ^ {- \alpha } dt $$
holds. By expanding $ ( 1 - tz) ^ {- \alpha } $ into a binomial series and using contour integrals for the beta-function, other integral representations can be obtained [2]. The integral (3) and other similar formulas defining an analytic function of $ z $ which is single-valued throughout the $ z $-plane can also be used as analytic continuations of $ F ( \alpha , \beta ; \gamma ; z) $ into the domain $ | \mathop{\rm arg} (- z) | < \pi $. Other analytic continuations also exist [1], [2].
The asymptotic behaviour of hypergeometric functions for large values of $ | z | $ is completely described by formulas yielding analytic continuations in a neighbourhood of the point $ z = \infty $ [1], [2], [3]. If $ \alpha $, $ \beta $ and $ z $ are given and $ | \gamma | $ is sufficiently large, $ | \mathop{\rm arg} \gamma | < ( \pi - \epsilon ) $, $ \epsilon > 0 $, then, if $ | z | < 1 $:
$$ F ( \alpha , \beta ; \gamma ; z) = \ \sum _ {k = 0 } ^ { n } \frac{( \alpha ) _ {k} ( \beta ) _ {k} }{( \gamma ) _ {k} } \frac{z ^ {k} }{k!} + O ( | \gamma | ^ {- n + 1 } ). $$
A similar expression is obtained for $ | z | > 1 $.
For fixed $ \alpha $, $ \gamma $ and $ z $, $ \gamma \neq 0, - 1, - 2 \dots $ $ 0 < | z | < 1 $, and $ \beta \rightarrow \infty $, $ - 3 \pi /2 < \mathop{\rm arg} \beta z < \pi /2 $,
$$ F ( \alpha , \beta ; \gamma ; z) = \ F \left ( \alpha , \beta ; \gamma ; \ \frac{\beta z } \beta \right ) = $$
$$ = \ \left [ \sum _ {n = 0 } ^ \infty \frac{( \alpha ) _ {n} ( \beta ) _ {n} }{( \gamma ) _ {n} n! } \right ] [ 1 + O ( | \beta | ^ {- 1} )]. $$
Representation of functions by hypergeometric functions. The elementary functions:
$$ ( 1 + z) ^ {n} = \ F (- n, 1; 1; - z), $$
$$ \mathop{\rm ln} \frac{1 + z }{1 - z } = 2zF \left ( { \frac{1}{2} } , 1; { \frac{3}{2} } ; z ^ {2} \right ) , $$
$$ \mathop{\rm ln} ( 1 + z) = zF ( 1, 1; 2; - z), $$
$$ e ^ {z} = \lim\limits _ {b \rightarrow \infty } F \left ( 1, b; 1; { \frac{z}{b} } \right ) , $$
$$ \mathop{\rm arc} \sin z = zF \left ( { \frac{1}{2} } ,\ { \frac{1}{2} } ; { \frac{3}{2} } ; z ^ {2} \right ) , $$
$$ \mathop{\rm arc} \mathop{\rm tan} z = zF \left ( { \frac{1}{2} } , 1; { \frac{3}{2} } ; - z ^ {2} \right ) , $$
$$ \sin nz = n \sin z F \left ( \frac{1 + n }{2} , { \frac{1 - n }{2} } ; { \frac{3}{2} } ; \sin ^ {2} z \right ) , $$
$$ \cos nz = F \left ( { \frac{1}{2} } n, - { \frac{1}{2} } n; { \frac{1}{2} } ; \sin ^ {2} z \right ) . $$
The complete elliptic integrals of the first and second kinds (cf. Elliptic integral):
$$ K ( z) = { \frac \pi {2} } F \left ( { \frac{1}{2} } , { \frac{1}{2} } ; 1; z ^ {2} \right ) , $$
$$ E ( z) = { \frac \pi {2} } F \left ( - { \frac{1}{2} } , { \frac{1}{2} } ; 1; z ^ {2} \right ) . $$
The adjoint Legendre functions:
$$ P _ {n} ^ {m} ( z) = \ \frac{( z + 1) ^ {m / 2 } }{( z - 1) ^ {m / 2 } } { \frac{1}{\Gamma ( 1 - m) } } F \left ( - n, n + 1; 1 - m; { \frac{1 - z }{2} } \right ) . $$
$$ T _ {n} ( z) = F \left ( - n, n; { \frac{1}{2} } ; { \frac{1 - z }{2} } \right ) . $$
The Legendre polynomials:
$$ P _ {n} ( z) = F \left ( - n, n + 1; 1; { \frac{1 - z }{2} } \right ) . $$
The ultraspherical polynomials:
$$ \frac{n!}{{( 2a)} _ {n} } C _ {n} ^ {( a)} ( z) = F \left ( - n, n + 2a; a + { \frac{1}{2} } ; { \frac{1 - z }{2} } \right ) . $$
The Jacobi polynomials:
$$ \frac{n! }{( a + 1) _ {n} } P _ {n} ^ {( a, b) } ( z) = F \left ( - n, a + 1 + b + n; a + 1; { \frac{1 - z }{2} } \right ) . $$
Generalizations of hypergeometric functions. The generalized hypergeometric function
$$ {} _ {p} F _ {q} ( \alpha _ {1} \dots \alpha _ {p} ; \ \gamma _ {1} \dots \gamma _ {q} ; z) = \ \sum _ {n = 0 } ^ \infty { \frac{1}{n!} } \frac{( \alpha _ {1} ) _ {n} \dots ( \alpha _ {p} ) _ {n} }{( \gamma _ {1} ) _ {n} \dots ( \gamma _ {q} ) _ {n} } z ^ {n} $$
is said to be the solution of the hypergeometric equation of order $ q + 1 $ [2]. There are also other generalizations of hypergeometric functions, such as generalizations to include the case of several variables [2].
References
| [1] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
| [3] | I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1980) (Translated from Russian) |
| [4] | E.E. Kummer, "Ueber die hypergeometrische Reihe 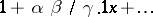 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 |
| [5] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [6] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) |
| [7] | A.L. Lebedev, R.M. Fedorova, "Handbook of mathematical tables" , Moscow (1956) (In Russian) |
| [8] | N.M. Burunova, "Handbook of mathematical tables" , Moscow (1959) (In Russian) (Supplement I) |
| [9] | A.A. Fletcher, J.C.P. Miller, L. Rosenhead, L.J. Comrie, "An index of mathematical tables" , 1–2 , Oxford Univ. Press (1962) |
Comments
To the list of functions representable by hypergeometric functions the Jacobi functions should be added:
$$ \phi _ \lambda ^ {( \alpha , \beta ) } ( z) = \ F \left ( { \frac{\alpha + \beta + 1 + i \lambda }{2} } ,\ { \frac{\alpha + \beta + 1 - i \lambda }{2} } ; \ \alpha + 1; - \sinh ^ {2} z \right ) , $$
cf. [a2].
An important generalization is given by the basic hypergeometric functions, cf. [a1].
References
| [a1] | G. Gasper, M. Rahman, "Basic hypergeometric series" , Cambridge Univ. Press (1989) |
| [a2] | T.H. Koornwinder, "Jacobi functions and analysis on noncompact semisimple Lie groups" R.A. Askey (ed.) T.H. Koornwinder (ed.) W. Schempp (ed.) , Special functions: group theoretical aspects and applications , Reidel (1984) pp. 1–85 |
Hypergeometric function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypergeometric_function&oldid=51949