Hyperbolic paraboloid
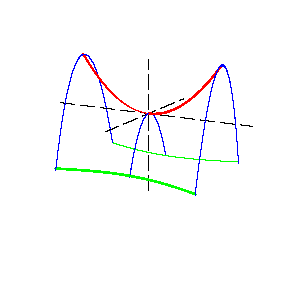
A non-closed non-central surface of the second order. In a suitable coordinate system (see Figure 1) the equation of a hyperbolic paraboloid is \begin{equation} \frac{x^2}{p}-\frac{y^2}{q}=2z, \qquad\text{where}\;p,q>0. \end{equation} Sections of a hyperbolic paraboloid by planes parallel to the planes $xOz$ and $yOz$ are parabolas, while sections by planes parallel to the plane $xOy$ are hyperbolas (the section by the plane $xOy$ consists of two straight lines). The symmetry axis of a hyperbolic paraboloid is said to be its axis; the point of intersection of a hyperbolic paraboloid with the axis is known as the apex. If $p=q$, the hyperbolic paraboloid has two axes of symmetry.
A hyperbolic paraboloid is a ruled surface; the equations of the rectilinear generators passing through a given point $(x_0,y_0,z_0)$ have the form \begin{equation} \begin{aligned} \frac{x-x_0}{\sqrt{p}}=\frac{y-y_0}{\sqrt{q}}=\frac{z-z_0}{\frac{x_0}{\sqrt{p}}-\frac{y_0}{\sqrt{q}}}, \\ \frac{x-x_0}{\sqrt{p}}=\frac{y-y_0}{-\sqrt{q}}=\frac{z-z_0}{\frac{x_0}{\sqrt{p}}-\frac{y_0}{\sqrt{q}}}. \end{aligned} \end{equation}
References
| [1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
Hyperbolic paraboloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_paraboloid&oldid=38839