Hopf bifurcation
Consider an autonomous system of ordinary differential equations depending on a parameter
$$ \tag{a1 } {\dot{x} } = f ( x, \alpha ) , \quad x \in \mathbf R ^ {n} , \alpha \in \mathbf R ^ {1} , $$
where $ f $ is a smooth function. Suppose that at $ \alpha = 0 $, the system (a1) has an equilibrium position $ x = 0 $ with a simple pair of purely imaginary eigenvalues $ \lambda _ {1,2 } = \pm i \omega _ {0} $, $ \omega _ {0} > 0 $, of its Jacobian matrix $ A = f _ {x} ( 0,0 ) $. Then, generically, a unique limit cycle bifurcates from the equilibrium while it changes stability, as $ \alpha $ passes through $ \alpha = 0 $. This phenomenon is called the Hopf (or Andronov–Hopf) bifurcation [a1], [a7], [a2], [a3]. It is characterized by a single bifurcation condition $ { \mathop{\rm Re} } \lambda _ {1,2 } = 0 $( has codimension one) and appears generically in one-parameter families.
First, consider a smooth planar system
$$ \tag{a2 } {\dot{x} } = f ( x, \alpha ) , \quad x \in \mathbf R ^ {2} , \alpha \in \mathbf R ^ {1} , $$
that has for all sufficiently small $ | \alpha | $ the equilibrium $ x = 0 $ with eigenvalues $ \lambda _ {1,2 } ( \alpha ) = \mu ( \alpha ) \pm i \omega ( \alpha ) $, $ \mu ( 0 ) = 0 $, $ \omega ( 0 ) = \omega _ {0} > 0 $. If the following non-degeneracy (genericity) conditions hold:
1) $ l _ {1} ( 0 ) \neq 0 $, where $ l _ {1} ( \alpha ) $ is the first Lyapunov coefficient (see below);
2) $ \mu ^ \prime ( 0 ) \neq 0 $, then (a2) is locally topologically equivalent (cf. Equivalence of dynamical systems) near the origin to the normal form
$$ \tag{a3 } \left \{ \begin{array}{l} { {\dot{y} } _ {1} = \beta y _ {1} - y _ {2} + \sigma y _ {1} ( y _ {1} ^ {2} + y _ {2} ^ {2} ) , \ } \\ { {\dot{y} } _ {2} = y _ {1} + \beta y _ {2} + \sigma y _ {2} ( y _ {1} ^ {2} + y _ {2} ^ {2} ) , \ } \end{array} \right . $$
where $ y = ( y _ {1} ,y _ {2} ) ^ {T} \in \mathbf R ^ {2} $, $ \beta \in \mathbf R ^ {1} $, $ \sigma = { \mathop{\rm sign} } l _ {1} ( 0 ) = \pm 1 $( see [a2], [a6]).

Figure: h110260a
Supercritical Hopf bifurcation on the plane
Consider the case $ \sigma = - 1 $. Then the system (a3) has an equilibrium at the origin $ x = 0 $, which is stable for $ \beta \leq 0 $( weakly at $ \beta = 0 $) and unstable for $ \beta > 0 $. Moreover, there is a unique and stable circular limit cycle that exists for $ \beta > 0 $ and has radius $ \sqrt \beta $( see Fig.a1). This is a supercritical Hopf bifurcation.
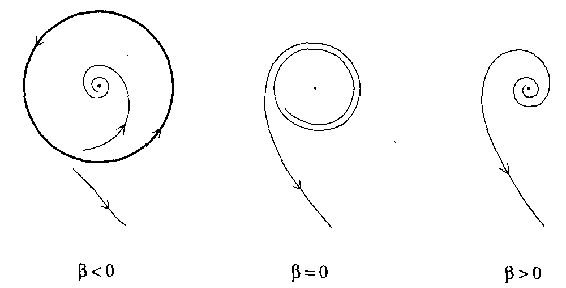
Figure: h110260b
Subcritical Hopf bifurcation on the plane
For $ \sigma = 1 $, the origin in (a3) is stable for $ \beta < 0 $ and unstable for $ \beta \geq 0 $( weakly at $ \beta = 0 $), while a unique and unstable limit cycle exists for $ \beta < 0 $( see Fig.a2). This is a subcritical Hopf bifurcation.
In the $ n $- dimensional case, the Jacobian matrix $ A $ evaluated at the equilibrium $ x = 0 $ has a simple pair of purely imaginary eigenvalues $ \lambda _ {1,2 } = \pm \omega _ {0} $, $ \omega _ {0} > 0 $, as well as $ n _ {s} $ eigenvalues with $ { \mathop{\rm Re} } \lambda _ {j} < 0 $, and $ n _ {u} $ eigenvalues with $ { \mathop{\rm Re} } \lambda _ {j} > 0 $( $ n _ {s} + n _ {u} + 2 = n $). According to the centre manifold theorem (cf. Centre manifold) [a5], [a7], [a2], there is an invariant two-dimensional centre manifold $ {\mathcal M} _ \alpha $ near the origin, the restriction of (a1) to which has the form (a2). Moreover, [a2], under the non-degeneracy conditions 1) and 2), the system (a1) is locally topologically equivalent (cf. Equivalence of dynamical systems) near the origin to the suspension of the normal form (a3) by the standard saddle:
$$ \tag{a4 } \left \{ \begin{array}{l} { {\dot{y} } _ {1} = \beta y _ {1} - y _ {2} + \sigma y _ {1} ( y _ {1} ^ {2} + y _ {2} ^ {2} ) , \ } \\ { {\dot{y} } _ {2} = y _ {1} + \beta y _ {2} + \sigma y _ {2} ( y _ {1} ^ {2} + y _ {2} ^ {2} ) , \ } \\ { {\dot{y} } _ {s} = - y _ {s} , \ } \\ { {\dot{y} } _ {u} = + y _ {u} , \ } \\ \end{array} \right . $$
where $ \beta \in \mathbf R ^ {1} $, $ y = ( y _ {1} ,y _ {2} ) ^ {T} \in \mathbf R ^ {2} $, $ y _ {s} \in \mathbf R ^ {n _ {s} } $, $ y _ {u} \in \mathbf R ^ {n _ {u} } $. Fig.a3 shows the phase portraits of the system (a4) in the three-dimensional case, when $ n = 3 $, $ n _ {s} = 1 $, $ n _ {u} = 0 $, and $ \sigma = - 1 $.
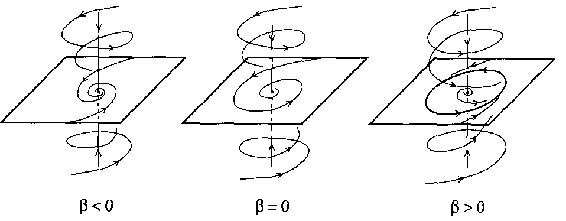
Figure: h110260c
Hopf bifurcation in $ \mathbf R ^ {3} $
The first Lyapunov coefficient $ l _ {1} ( 0 ) $ can be computed (to within a scalar multiple) in terms of the right-hand side of (a1) at $ \alpha = 0 $. Represent $ f ( x,0 ) $ as
$$ f ( x,0 ) = Ax + { \frac{1}{2} } B ( x,x ) + { \frac{1}{6} } C ( x,x,x ) + O ( \left \| x \right \| ^ {4} ) , $$
where $ B ( x,y ) $ and $ C ( x,y,z ) $ are multilinear functions (cf. also Multilinear mapping). In coordinates one has
$$ B _ {i} ( x,y ) = \sum _ {j,k = 1 } ^ { n } \left . { \frac{\partial ^ {2} f _ {i} ( \xi,0 ) }{\partial \xi _ {j} \partial \xi _ {k} } } \right | _ {\xi = 0 } x _ {j} y _ {k} , $$
$$ C _ {i} ( x,y,z ) = \sum _ {j,k,l = 1 } ^ { n } \left . { \frac{\partial ^ {3} f _ {i} ( \xi,0 ) }{\partial \xi _ {j} \partial \xi _ {k} \partial \xi _ {l} } } \right | _ {\xi = 0 } x _ {j} y _ {k} z _ {l} , $$
where $ i = 1 \dots n $. Let $ q $ be a complex eigenvector of $ A $ corresponding to the eigenvalue $ i \omega _ {0} $:
$$ Aq = i \omega _ {0} q, \quad q \in \mathbf C ^ {n} . $$
Introduce also the adjoint eigenvector $ p $:
$$ A ^ {T} p = - i \omega _ {0} p, \quad \left \langle {p,q } \right \rangle = 1, $$
where $ \langle {p,q } \rangle = \sum _ {j = 1 } ^ {n} {\overline{p}\; } _ {j} q _ {j} $ is the inner product in $ \mathbf C ^ {n} $. Then (see, for example, [a6])
$$ l _ {1} ( 0 ) = $$
$$ = { \frac{1}{2 \omega _ {0} } } { \mathop{\rm Re} } \left [ \left \langle {p,C ( q,q, {\overline{q}\; } ) } \right \rangle - 2 \left \langle {p,B ( q,A ^ {- 1 } B ( q, {\overline{q}\; } ) ) } \right \rangle \right . + $$
$$ + \left . \left \langle {p,B ( {\overline{q}\; } , ( 2i \omega _ {0} I _ {n} - A ) ^ {- 1 } B ( q,q ) ) } \right \rangle \right ] . $$
There is an analogue of the Hopf bifurcation for discrete-time dynamical systems, called the Neimark–Sacker bifurcation [a7], [a4], [a2], [a8], [a6]. Under certain non-degeneracy conditions, it generates a closed invariant curve around a fixed point which changes stability due to the transition of a pair of its complex eigenvalues through the unit circle.
References
| [a1] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Theory of bifurcations of dynamical systems on a plane" , Israel Program Sci. Transl. (1971) (In Russian) |
| [a2] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Grundlehren math. Wiss. , 250 , Springer (1983) (In Russian) |
| [a3] | J. Guckenheimer, Ph. Holmes, "Nonlinear oscillations, dynamical systems and bifurcations of vector fields" , Springer (1983) |
| [a4] | G. Iooss, "Bifurcations of maps and applications" , North-Holland (1979) |
| [a5] | A. Kelley, "The stable, center stable, center, center unstable and unstable manifolds" J. Diff. Eq. , 3 (1967) pp. 546–570 |
| [a6] | Yu.A. Kuznetsov, "Elements of applied bifurcation theory" , Springer (1995) |
| [a7] | J. Marsden, M. McCracken, "Hopf bifurcation and its applications" , Springer (1976) |
| [a8] | D.C. Whitley, "Discrete dynamical systems in dimensions one and two" Bull. London Math. Soc. , 15 (1983) pp. 177–217 |
Hopf bifurcation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_bifurcation&oldid=47268