Holomorphically-convex complex space
A complex space $ X $
that satisfies the following condition: For each compactum $ K \subset X $
the set
$$ \left \{ {x \in X } : {| f ( x) | \leq \sup _ { K } | f | ( f \in A) } \right \} , $$
where $ A $ is the algebra of holomorphic functions on $ X $, is compact. A space $ X $ is holomorphically convex if and only if it admits a proper surjective holomorphic mapping $ \phi $ onto some Stein space (a holomorphically-complete space) $ \widetilde{X} $ which induces an isomorphism between the algebras of holomorphic functions on these spaces. The mapping $ \phi : X \rightarrow \widetilde{X} $( the holomorphic reduction of $ X $) is uniquely defined and has connected fibres [1]. For any coherent analytic sheaf $ F $ on a holomorphically-convex complex space $ X $, the cohomology spaces $ H ^ {p} ( X, F ) $ and $ H _ {c} ^ {p} ( X, F ) $, $ p \geq 0 $, are separable topological vector spaces [2].
A special class of holomorphically-convex complex spaces is formed by the complex spaces $ X $ for which the holomorphic reduction mapping is bijective outside some compact analytic set (such a space is obtained from a Stein space by a proper modification which blows-up a finite number of points). A complex space possesses this property if and only if
$$ \mathop{\rm dim} H ^ {p} ( X, F ) < \infty ,\ \ p > 0, $$
for any coherent analytic sheaf $ F $ on $ X $[3]. This class of complex spaces also coincides with the class of strictly $ 1 $- convex complex spaces (cf. Pseudo-convex and pseudo-concave).
References
| [1] | H. Cartan, "Quotients of complex analytic spaces" , Contributions to function theory. Internat. Colloq. Function Theory, Bombay 1960 , Tata Inst. (1960) pp. 1–15 |
| [2] | J.P. Ramis, "Théorèmes de séperation et de finitude pour l'homologie et la cohomologie des espaces 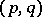 -convexes-concaves" Ann. Scuola Norm. Sup. Pisa Ser. 3 , 27 (1973) pp. 933–997 -convexes-concaves" Ann. Scuola Norm. Sup. Pisa Ser. 3 , 27 (1973) pp. 933–997 |
| [3] | R. Narasimhan, "The Levi problem for complex spaces II" Math. Ann. , 146 (1962) pp. 195–216 |
Comments
References
| [a1] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) pp. Chapt. 1, Sect. G |
| [a2] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German) |
| [a3] | H. Grauert, R. Remmert, "Komplexe Räume" Math. Ann. , 136 (1958) pp. 245–318 |
Holomorphically-convex complex space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holomorphically-convex_complex_space&oldid=47246